4.26. Low Density Foam Model

4.26.1. Theory

The low density foam material model is a phenomenological model for rigid, low density polyurethane foams. Development of this model followed extensive characterization efforts at Sandia National Laboratory with special emphasis placed on hydrostatic and triaxial compression tests [[1]]. A key observation of this investigation was the impact of trapped air inside the foam on the load bearing capabilities of the material.

In constructing a model describing the response of the low-density foams, Neilsen et al. [[1]] decomposed the response into that of the polymeric skeleton and the air such that,

(4.119)\[\sigma_{ij}=\sigma_{ij}^{\text{sk}} + \sigma^{\text{air}}\delta_{ij},\]

where the super script sk is used to refer to variables relating to the skeleton and air to the air. The contribution of the air component is only present, however, in constrained cases when the internal gases are trapped and not allowed to escape. If the foam material in not encased or encapsulated in someway, the air may escape and \(\sigma^{\text{air}}=0\). A model parameter, \(N_{\text{air}}\), is included to distinguish between these cases. If \(N_{\text{air}}\) is set to \(0\), the air pressure term is set to zero. For any other value, it is included.

Using the ideal gas law, it can be found that for an isothermal case,

(4.120)\[\sigma^{\text{air}}=\frac{p_{0}\varepsilon_{\text{V}}}{\varepsilon_{\text{V}}+1-\phi},\]

where \(p_{0}\), \(\varepsilon_{\text{V}}\), and \(\phi\) are the initial air pressure, volumetric strain, and the volume fraction of the solid (skeleton) material. Knowing the total stress of the material volume and air contribution, the skeleton stress may be found via (4.119). Furthermore, it should be noted that the foam (total) and skeleton strains are the same.

Based on their experimental observations, Neilsen et al. [[1]] noted a decoupling between the skeleton principal stresses. Therefore, the Poisson’s ratio of the skeleton is zero and that the yielding behavior in each principal direction is independent. A yield function of the form,

\[f_i=\sigma^{\text{sk}}_i-\bar{\sigma},\]

where \(f_i\) and \(\sigma^{\text{sk}}_i\) are the \(i^{th}\) yield function and skeleton principal stress, respectively, and

(4.121)\[\bar{\sigma} = A \left< I_{2}^{\prime} \right> + B \left( 1.0 + C \varepsilon_{V} \right)\]

with A, B, and C are material parameters, and \(\left< \cdot \right>\) denoting the Heaviside step function where

(4.122)\[\begin{split}\left< x \right> = \begin{cases} 0 \;\;\; \text{if } x \leq 0 \\ 1 \;\;\; \text{if } x > 0 \end{cases},\end{split}\]

was proposed. Additionally, \(I_{2}^{\prime}\) is the second invariant of the deviatoric strain. If a skeleton principal stress indicates yielding, it is set to the effective yield stress value, \(\bar{\sigma}\).

4.26.2. Implementation

The low density foam material model is implemented in a hypoelastic fashion. Therefore, a trial material state of,

(4.123)\[\begin{split}T^{\text{sk}-tr}_{ij}=T^{\text{sk}-n}_{ij}+E\Delta td_{ij}, \\ \varepsilon^{n+1}_{ij}=\varepsilon^n_{ij}+\Delta td_{ij},\end{split}\]

with \(d_{ij}\), \(T^{\text{sk}}_{ij}\), and \(\varepsilon_{ij}\) are the unrotated rate of deformation, unrotated skeleton stress, and foam strain, respectively, is calculated. The superscript \(tr\) denotes a trial stress while \(E\) is the Young’s Modulus and (4.123) leverages the fact that the Poisson’s ratio of the skeleton is zero. The principal stresses of the trial skeleton stress state, \(T^{\text{sk}-tr}_i\), are then computed via the algorithm of Scherzinger and Dohrmann [[2]].

To check the yielding behavior, the (logarithmic) volumetric strain, \(\varepsilon^{n+1}_{\text{V}}\), and second invariant of the deviatoric strain, \(I_2'\), are needed. These values are simply calculated as,

\[\begin{split}\varepsilon_{\text{V}}^{n+1} & = \exp\left(\varepsilon^{n+1}_{kk}\right)-1, \\ I'^{n+1}_2 & = \hat{\varepsilon}_{11}^{n+1}\hat{\varepsilon}_{22}^{n+1} +\hat{\varepsilon}_{11}^{n+1}\hat{\varepsilon}_{33}^{n+1} +\hat{\varepsilon}_{22}^{n+1}\hat{\varepsilon}_{33}^{n+1} -\left[\left(\hat{\varepsilon}^{n+1}_{12}\right)^2 + \left(\hat{\varepsilon}^{n+1}_{23}\right)^2 +\left(\hat{\varepsilon}^{n+1}_{31}\right)^2\right],\end{split}\]

with \(\hat{\varepsilon}^{n+1}_{ij}\) being the deviatoric strain tensor. The effective yield stress, \(\bar{\sigma}^{n+1}\), may be written as,

\[\bar{\sigma}^{n+1}=A\left<I'^{n+1}_2\right>+B\left(1+C\varepsilon^{n+1}_{\text{V}}\right).\]

It should also be noted that a steep sinusoidal approximation of the Heaviside step function to alleviate numerical issues associated with the sharp discontinuity inherit to the use of the Heaviside function. The updated principal stresses may then be determined as,

\[\begin{split}T^{\text{sk}-n+1}_i=\left\{\begin{array}{cc} T^{\text{sk}-tr}_i, & |T^{\text{sk}-tr}_i| \leq |\bar{\sigma}| \\ \text{sgn}\left(T^{\text{sk}-tr}_i\right)\bar{\sigma}, & |T^{\text{sk}-tr}_i| > |\bar{\sigma}| \end{array} \right. ,\end{split}\]

where \(\text{sgn}\left(x\right)\) denotes the sign of \(x\). An updated air pressure is then computed from (4.120) and the current stress is found to be,

\[T^{n+1}_{ij}=\sum_{k=1}^3T^{\text{sk}-n+1}_k\hat{e}^k_i\hat{e}^k_j+\sigma^{\text{air}-n+1}\left(\varepsilon_{\text{V}}^{n+1}\right)\delta_{ij},\]

where \(\hat{e}^k_i\) is the eigenvector associated with the \(k^{th}\) principal skeleton stress.

4.26.3. Verification

The low density foam model is implemented through two compression tests – uniaxial and hydrostatic. Cases both including (\(N_{\text{air}}=1.0\)) and excluding (\(N_{\text{air}}=0.0\)) the contribution of the air are investigated. The rest of the properties and parameters used for these tests are given in Table 4.39 and are originally from [[3]].

Table 4.39 Material properties and model parameters for the low density foam model used during verification testing.

\(E\)	3010 psi	\(\nu\)	0.0
\(A\)	49.2 psi	\(B\)	60.8 psi
\(C\)	-0.517	\(p_0\)	14.7 psi
\(\phi\)	0.09

4.26.3.1. Uniaxial Compression

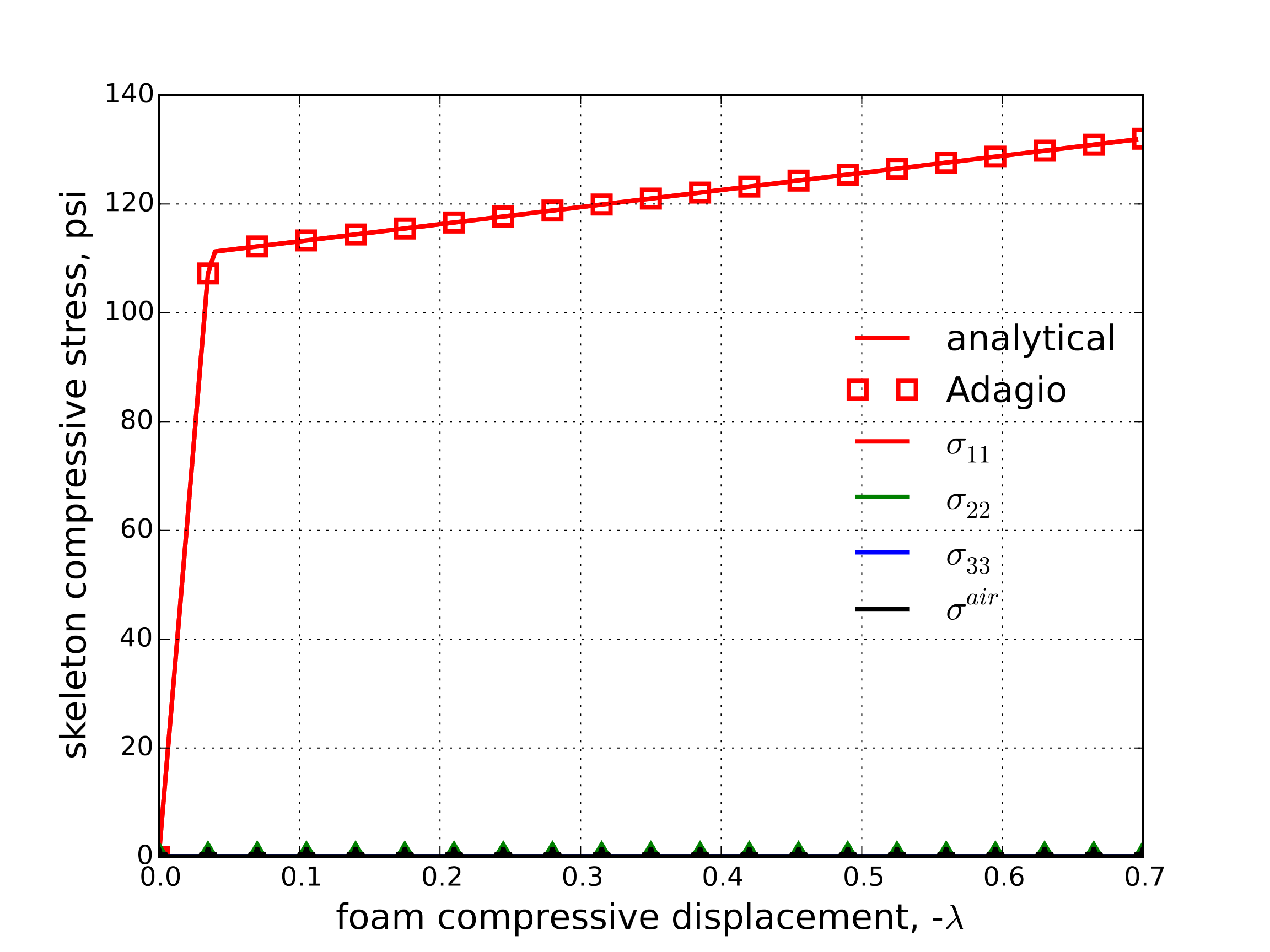
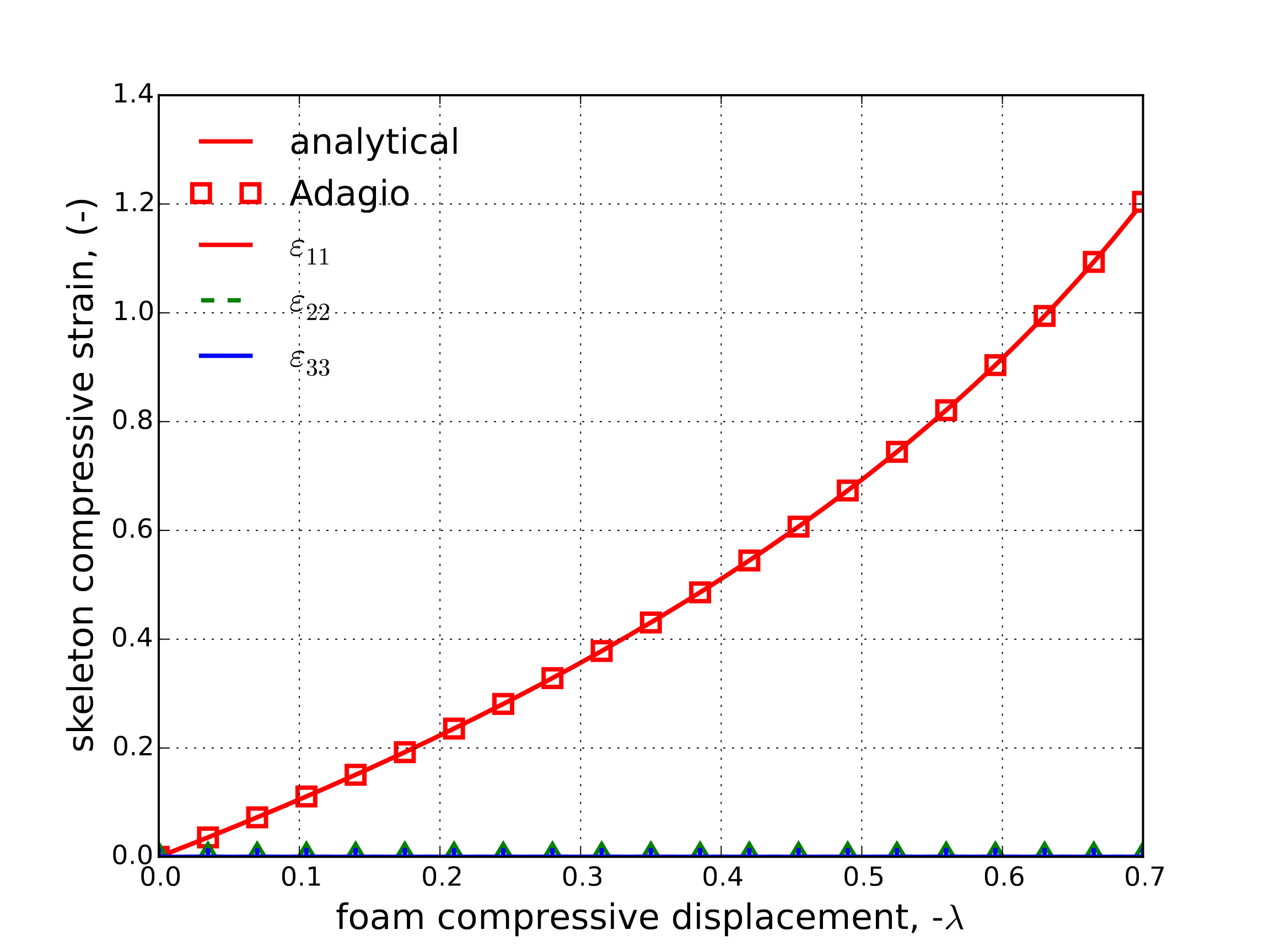
First, a uniaxial compression test under displacement control is considered with and without the contribution of air. In this case, a displacement of the form \(u_1=\lambda\) is applied while the other two directions are left traction free. When air pressure does not play a role, the model response reduces to that of the skeleton and the problem becomes one-dimensional. The deformation rate can be easily integrated to find that \(\varepsilon_{11}=\ln\left(1+\lambda\right)\) and \(\varepsilon_{\text{V}}=\lambda\). Additionally, the uniaxial compression loading considered here is obviously deviatoric in nature leading to \(\left<I_2'\right>\) evaluating to 1. Therefore,

(4.124)\[\begin{split}\bar{\sigma} & = A + B\left(1+C\lambda\right), \\ \sigma_{11} & = \left\{\begin{array}{cc} E\varepsilon_{11} & |\sigma_{11}| \leq |\bar{\sigma}| \\ \text{sgn}\left(\varepsilon_{11}\right)\bar{\sigma} & |\sigma_{11}| > |\bar{\sigma}| \end{array} \right. .\end{split}\]

The corresponding stress and strain results are presented in Fig. 4.120(a) and Fig. 4.120(b).

Skeleton stress

Skeleton strain

Fig. 4.120 Skeleton (a) stress and (b) strain determined analytically and numerically (with \(N_{\text{air}}=0\)) with the low density foam model during a displacement controlled uniaxial compression test.

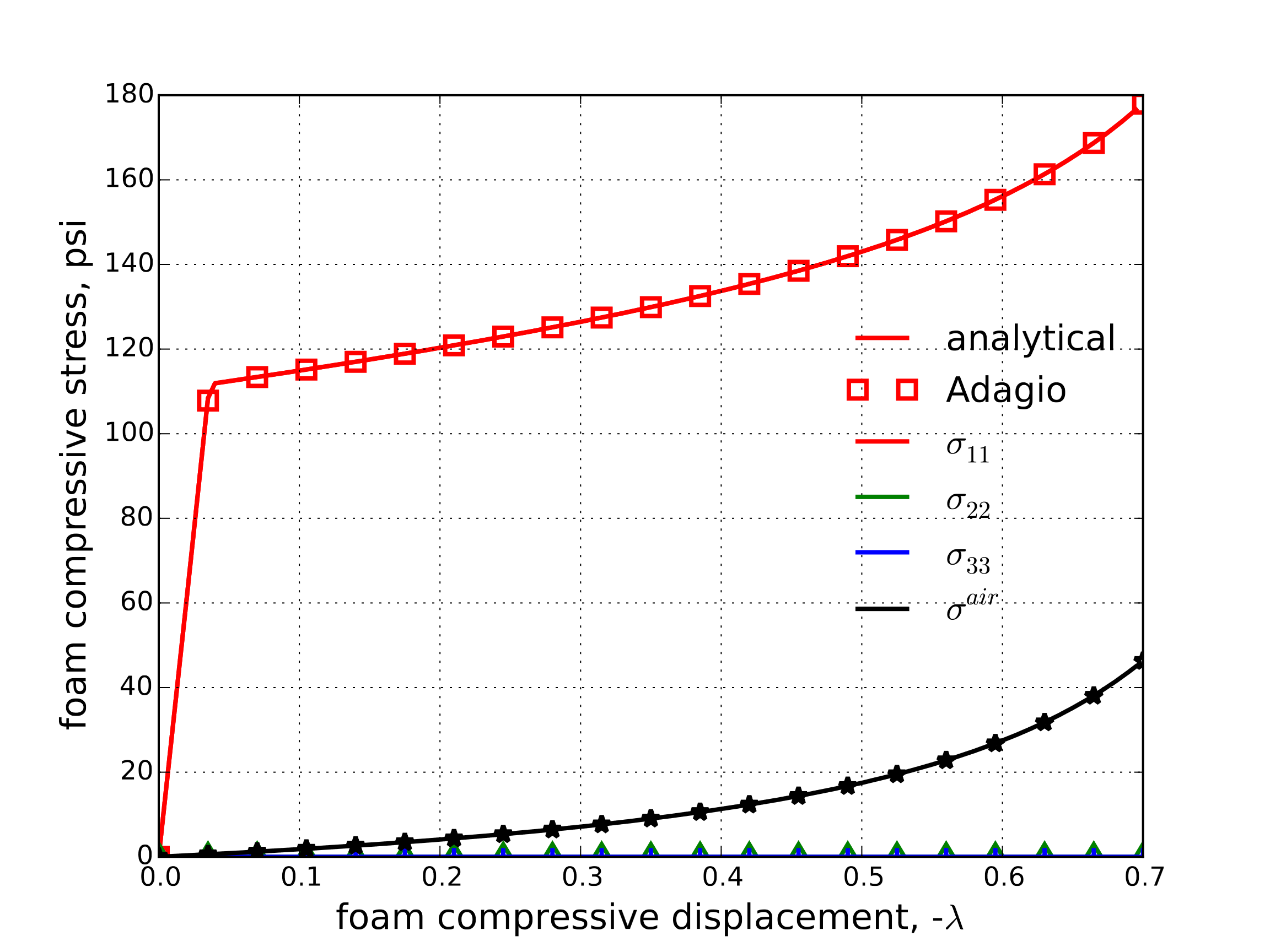
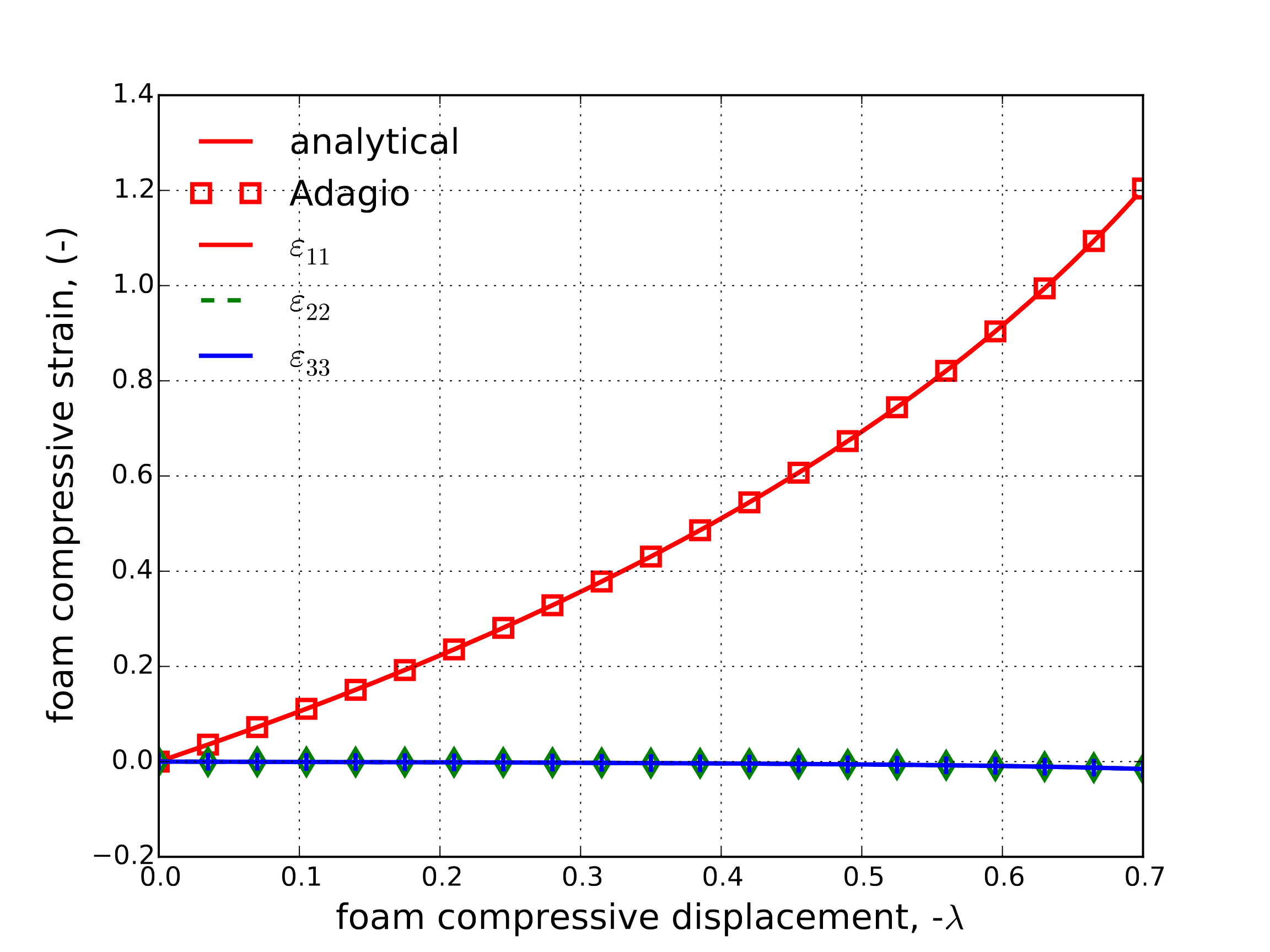
The case of internal air pressure is also considered by setting \(N_{\text{air}}=1\). This, however, complicates the response and turns it into a three-dimensional case given the pressure components in the off-loading directions. Specifically, it can be found trivially that, \(\varepsilon_{22}=\varepsilon_{33}=-\sigma^{\text{air}}/E\). The complication arises as the volumetric strain is now,

\[\varepsilon_{\text{V}}=\left(1+\lambda\right)\exp\left(-2\sigma^{\text{air}}/E\right)-1,\]

leading to an implicit expression for \(\sigma^{\text{air}}\). By evaluating \(\sigma^{\text{air}}\) in a forward Euler fashion, noting \(\bar{\sigma}=A+B\left(1+C\varepsilon_{\text{V}}\right)\), and treating (4.124) as an expression for \(\sigma^{\text{sk}}_{11}\) the stress and strain responses may be found as given in Fig. 4.121(a) and Fig. 4.121(b). The impact of the air on the model response is clear by comparing the two sets of figures.

Skeleton stress

Skeleton strain

Fig. 4.121 Foam (a) stress and (b) strain determined analytically and numerically (with \(N_{\text{air}}=1\)) with the load density foam model during a displacement controlled uniaxial compression test.

4.26.3.2. Hydrostatic Compression

The volumetric deformation capabilities of the model are also investigated through displacement controlled hydrostatic compression. Specifically, an imposed displacement of the form \(u_i=\lambda\) is considered. The resultant strain field is \(\varepsilon_{11}=\varepsilon_{22}=\varepsilon_{33}=\ln\left(1+\lambda\right)\) leading to a volumetric strain of the form \(\varepsilon_{\text{V}}=\left(1+\lambda\right)^3-1\). As there is no deviatoric deformation it is apparent that \(\left<I_2'\right>=0\). Therefore, the effective yield stress is \(\bar{\sigma}=B\left(1+C\varepsilon_{\text{V}}\right)\). Also noting that \(\sigma=\sigma_{11}=\sigma_{22}=\sigma_{33}\), the foam response through such a loading may easily be determined. The foam stress for both the with and without air case is presented in Fig. 4.122 along with \(\sigma^{\text{air}}\) for the appropriate case.

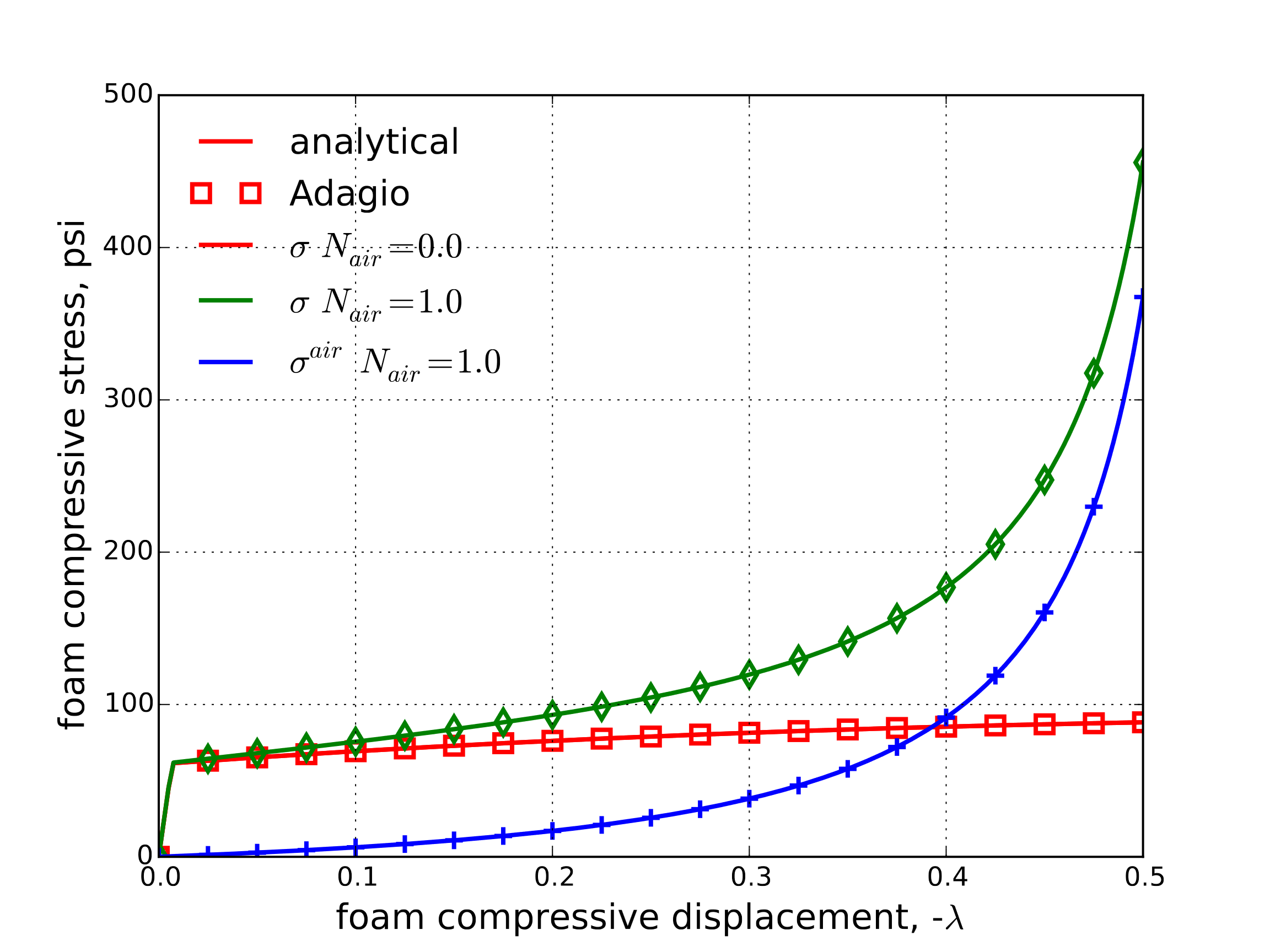
Fig. 4.122 Foam stress determined analytically and numerically for both \(N_{\text{air}}=0.0\) and \(N_{\text{air}}=1.0\) cases for the low density foam model during displacement controlled hydrostatic compression

4.26.4. User Guide

BEGIN PARAMETERS FOR MODEL LOW_DENSITY_FOAM
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  A    = <real>
  B    = <real>
  C    = <real>
  NAIR = <real>
  P0   = <real>
  PHI  = <real>
END [PARAMETERS FOR MODEL LOW_DENSITY_FOAM]

State variables for this model are listed in Table 4.40. For more information on the low density foam material model, see [[1]].

Table 4.40 State Variables for LOW DENSITY FOAM Model

Name	Description
PAIR	Air pressure

---

[1] (1,2,3,4)

M.K. Neilsen, H.S. Morgan, and R.D. Krieg. A phenomenological constitutive model for low density polyurethane foams. Technical Report SAND86-2927, Sandia National Laboratories, Albuquerque, NM, April 1987. \href http://infoserve.sandia.gov/sand_doc/1986/862927.pdfpdf.

[2]

W.M. Scherzinger and C.R. Dohrmann. A robust algorithm for finding the eigenvalues and eigenvectors of 3x3 symmetric matrices. Computer Methods in Applied Mechanics and Engineering, 197(45-48):4007–4015, 2008.

[3]

W.M. Scherzinger and D.C. Hammerand. Testing of constitutive models in LAME. Technical Report SAND2007-5872, Sandia National Laboratories, Albuquerque, NM, September 2007. \href http://infoserve.sandia.gov/sand_doc/2007/075872.pdfpdf.