Quantum computers have the potential to solve certain problems dramatically faster than is possible with classical computers. We are funded by the DOE Quantum Algorithms Teams program to explore the abilities of quantum computers in three interrelated areas: quantum simulation, optimization, and machine learning. We leverage connections among these areas and unearth deeper ones to fuel new applications of quantum information processing to science and technology.
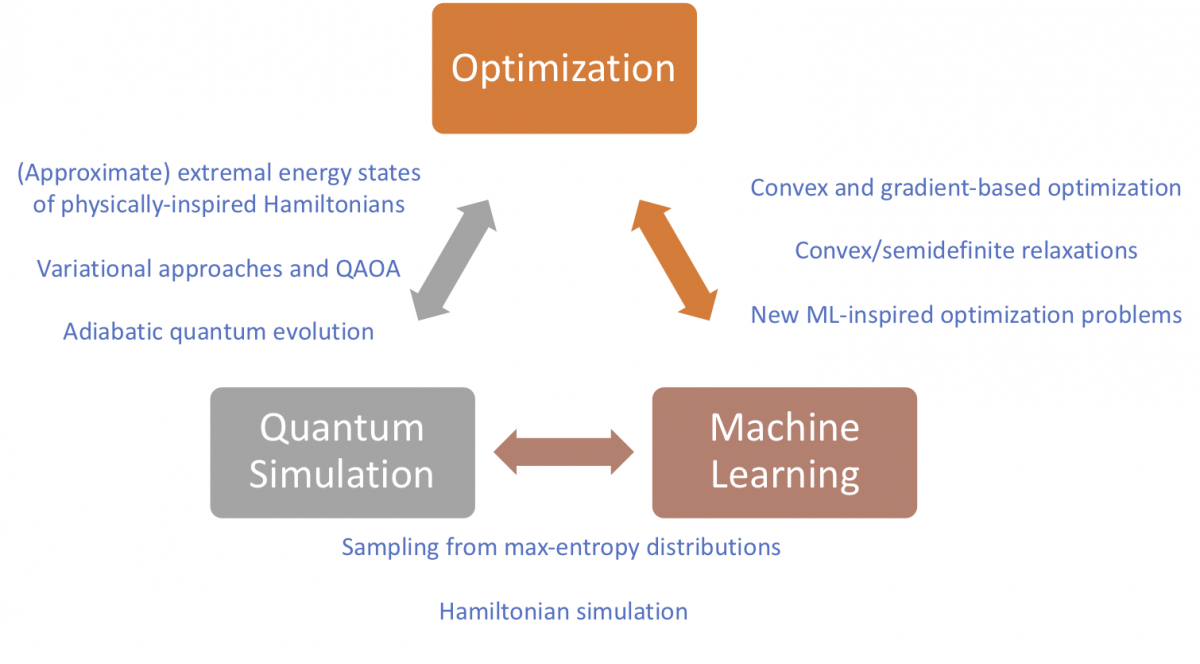
Quantum simulation
Quantum computers offer a natural approach to efficiently simulating the dynamics of quantum systems, a widely applicable problem that is intractable for classical computers. We aim to develop quantum algorithms for quantum simulation with improved performance and expanded scope. We also work extensively on applying quantum computation to problems in high-energy physics, where much work remains to develop simulations of general field theories.
Optimization
We seek to understand how quantum resources may be used to improve the quality of solutions over those produced by classical algorithms. We devise new quantum algorithms for approximating classical discrete optimization problems and ground states of physically motivated quantum Hamiltonians. Our approach is naturally amenable to a hybrid quantum/classical implementation.
Machine learning
By bringing together experts in classical machine learning and quantum computing, we aim to develop novel quantum machine learning algorithms with the potential for practical impact. We investigate quantum algorithms for decomposing tensors, which are ubiquitous in machine learning. We also expore generalizations of previous work on applications of Gibbs sampling to learning and quantum algorithms for learning from structured data.
Our Team
Sandia National Laboratories
- Ojas Parekh (Project Director). Quantum approaches to discrete optimization, Theoretical computer science
- Andrew Baczewski. Quantum and classical simulation of many-body quantum systems
- Matthew Grace
- Kenneth Rudinger. Quantum characterization, verification, and validation; Quantum algorithms
- Mohan Sarovar. Quantum control, Quantum dynamics
Los Alamos National Laboratory
- Rolando Somma. Quantum computing, Condensed matter
- Yigit Subasi
University of Maryland, College Park
- Andrew Childs. Quantum algorithms
- Stephen Jordan (also affiliated with Microsoft Research). Quantum algorithms for simulating and optimization, Quantum complexity theory
- Yi-Kai Liu (also affiliated with NIST). Quantum algorithms, Machine learning
- Brian Swingle. Quantum Many-Body Physics, Quantum Gravity
- Jacob Taylor (also affiliated with NIST). Quantum machine learning, Many-body quantum systems
- Xiaodi Wu. Quantum machine learning, Optimization
California Institute of Technology
- John Preskill
Virginia Commonwealth University
- Sevag Gharibian (also affiliated with Universität Paderborn, Germany)Quantum algorithms and complexity theory
