What is Synthetic Aperture Radar?
Environmental monitoring, earth-resource mapping, and military systems require broad-area imaging at high resolutions. Often, this imagery must be acquired at night or during inclement weather—Synthetic Aperture Radar (SAR) provides such a capability. SAR systems take advantage of the long-range propagation characteristics of radar signals and the complex information processing capability of modern digital electronics to provide high resolution imagery. SAR complements photographic and other optical imaging capabilities because it is not limited by the time of day or atmospheric conditions and the unique responses of terrain and cultural targets to radar frequencies.
SAR technology provides terrain structural information to geologists for mineral exploration, oil spill boundaries on water to environmentalists, sea state and ice hazard maps to navigators, and reconnaissance and targeting information to military and intelligence operations. There are many other applications for this technology. Some of these, particularly civilian, have not yet been adequately explored because lower cost electronics are just beginning to make SAR technology economical for smaller scale uses.
How Does Synthetic Aperture Radar (SAR) Work?
A detailed description of the theory of operation of SAR is complex and beyond the scope of this site. Instead, this article written by Sandia Technical Staff Armin W. Doerry and Fred M. Dickey is intended to give the reader an intuitive feel for how SAR works.
(Click here for a more detailed explanation of SAR) Consider an airborne SAR imaging perpendicular to the aircraft velocity as shown in the figure below. Typically, SAR produces a two-dimensional (2-D) image. One dimension in the image is called range (or cross track) and is a measure of the "line-of-sight" distance from the radar to the target. Range measurement and resolution are achieved in SAR in the same manner as most other radars: range is determined by measuring the time from transmission of a pulse to receiving the echo from a target, and, in the simplest form of SAR, range resolution is determined by the transmitted pulse width, i.e. narrow pulses yield fine range resolution.
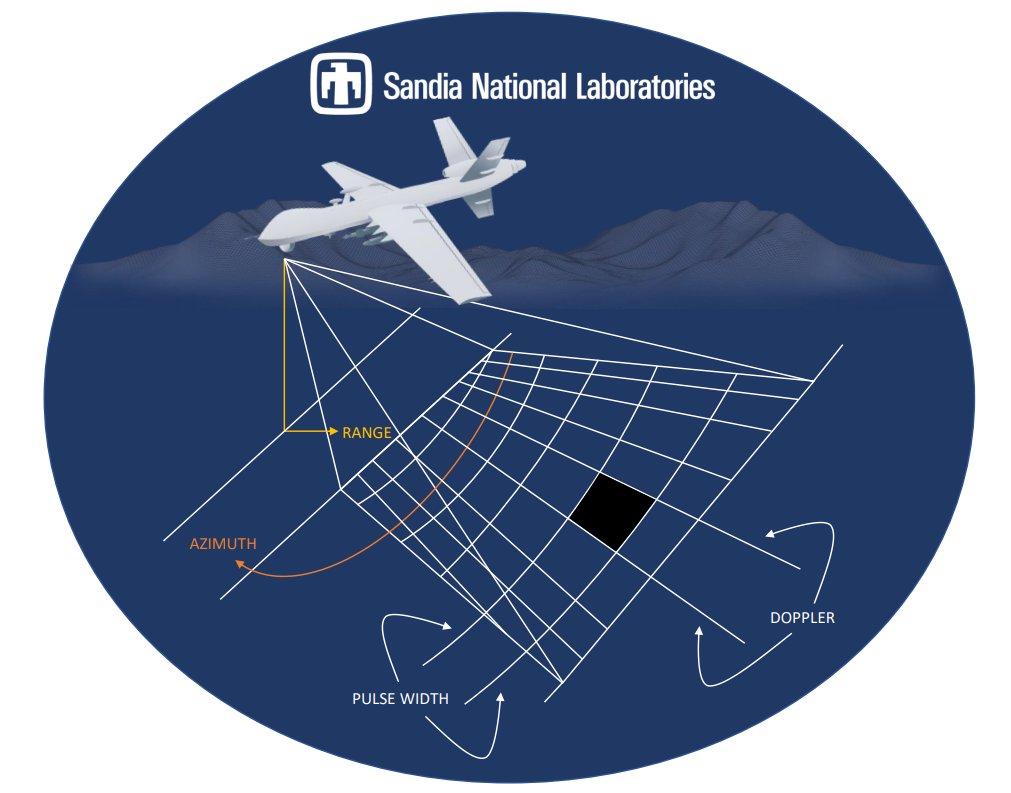
The other dimension is called azimuth (or along track) and is perpendicular to range. SAR’s ability to produce relatively fine azimuth resolution differentiates it from other radars. To obtain fine azimuth resolution, a physically large antenna is needed to focus the transmitted and received energy into a sharp beam. The sharpness of the beam defines the azimuth resolution. Similarly, optical systems, such as telescopes, require large apertures (mirrors or lenses which are analogous to the radar antenna) to obtain fine imaging resolution. Since SAR is much lower in frequency than optical systems, even moderate SAR resolutions require an antenna too large to be practically carried by an airborne platform; antenna lengths several hundred meters long are often required. However, airborne radar can collect data while flying this distance, and then process the data as if it came from a physically long antenna. The distance the aircraft flies in synthesizing the antenna is known as the synthetic aperture. A narrow synthetic beamwidth results from the relatively long synthetic aperture, which yields finer resolution than is possible from a smaller physical antenna.
Achieving fine azimuth resolution may also be described from a Doppler processing viewpoint. A target’s position along the flight path determines the Doppler frequency of its echoes. Targets ahead of the aircraft produce a positive Doppler offset, while targets behind the aircraft produce a negative offset. As the aircraft flies a distance (the synthetic aperture), echoes are resolved into a number of Doppler frequencies. The target’s Doppler frequency determines its azimuth position.
While this section attempts to provide an intuitive understanding, SARs are not as simple as described above. Transmitting short pulses to provide range resolution is generally not practical. Typically, longer pulses with wide-bandwidth modulation are transmitted, which complicate the range processing but decreases the peak power requirements on the transmitter. For even moderate azimuth resolutions, a target’s range to each location on the synthetic aperture changes along the synthetic aperture. The energy reflected from the target must be "mathematically focused" to compensate for the range dependence across the aperture prior to image formation. Additionally, for fine-resolution systems, the range and azimuth processing are coupled (dependent on each other) which also greatly increases the computational processing.
