From 2003 to 2009, I was a graduate student at the University of Illinois at Urbana-Champaign Department of Computer Science under the direction of Michael Heath. From 2003 to 2007, I was a Department of Energy Computational Science Graduate Fellow. My thesis was entitled "Hypergraph Based Combinatorial Optimization of Matrix-Vector Multiplication" and dealt primarily with two Combinatorial Scientific Computing problems. The unifying theme in the work was that for both problems I used graph and hypergraph models to improve the performance of important numerical kernels.
Two-Dimensional Sparse Matrix Partitioning

In work collaborating with Erik Boman at Sandia National Laboratories, we researched 2D partitioning of sparse matrices in order to improve the parallel performance of sparse matrix kernels such as matrix-vector multiplication. Typically people use 1D methods for partitioning sparse matrices. However, for certain problems these 1D partitions can result in high communication volumes in the parallel computation. In these cases, more general 2D methods are needed in order to obtain good parallel efficiency.
We developed two such 2D partitioning methods for sparse matrices. One of our methods, the nested dissection partitioning method, has been shown to be one of the best partitioning methods for sparse matrices from several application areas. This new method is competitive with the traditional best 2D algorithm (fine-grain hypergraph method) in terms of communication volume, but requires fewer messages and less time to obtain the partition. The nested dissection method is particularly effective on structurally symmetric matrices, where it is about as fast to compute as 1D methods and the communication volume is significantly reduced (up to 97%) compared to 1D layout. The plan is for these new methods (as well as previously developed methods) to be integrated into Isorropia, so they will be readily available for Trilinos users.
Optimization of Matrix-Vector Multiplication in Finite Element Assembly
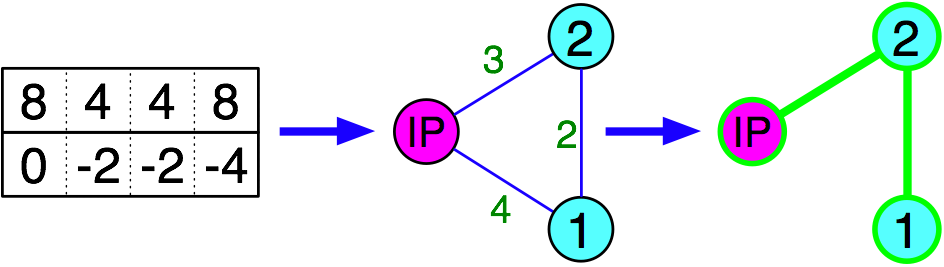
In previous work, Kirby et al. showed that combinatorial optimization of matrix-vector multiplication could lead to faster evaluation of finite element stiffness matrices. Based on a graph model characterizing relationships between rows, an efficient set of operations can be generated to perform matrix-vector multiplication for this problem. In our work, we improved the graph model by extending the set of binary row relationships and solved this combinatorial optimization problem optimally for the binary row relationships implemented, yielding significantly improved results over previous published graph models. We also extended the representation by using hypergraphs to model more complicated row relationships, expressing a three-row relationship with a three-vertex hyperedge, for example. Our initial greedy algorithm for this hypergraph model yielded significantly better results than the graph model for many matrices.
Papers
Michael M. Wolf, "Hypergraph-Based Combinatorial Optimization of Matrix-Vector Multiplication." PhD thesis, University of Illinois at Urbana-Champaign, July 2009.
Michael M. Wolf and Michael T. Heath, "Combinatorial Optimization of Matrix-Vector Multiplication in Finite Element Assembly," SIAM Journal on Scientific Computing, Volume 31, Issue 4, 2009, pp. 2960-2980.
Erik G. Boman and Michael M. Wolf, "A Nested Dissection Partitioning Method for Parallel Sparse Matrix-Vector Multiplication," IEEE HPEC 2013, Waltham, MA, September 2013.
M. M. Wolf, E.G. Boman, and B. Hendrickson, "Optimizing Parallel Sparse Matrix-Vector Multiplication by Corner Partitioning," PARA08, Trondheim, Norway, May 2008.
Michael M. Wolf and Erik G. Boman, "Partitioning for Parallel Sparse Matrix-Vector Multiplication," SANDIA Technical Report SAND2007-7977, Sandia National Laboratories, 2007, pp. 75-86.
J. Ray, B. M. Adams, K. D. Devine, Y. M. Marzouk, M. M. Wolf, and H. N. Najm, "Distributed Micro-Releases of Bioterror Pathogens: Threat Characterizations and Epidemiology from Uncertain Patient Observables," SANDIA Technical Report SAND2008-6044, Sandia National Laboratories.