Despite improved algorithms and the availability of massively parallel computing resources, “high-fidelity” models are, in practice, often too computationally expensive for use in a design or analysis setting. The continuing push to incorporate the quantification of uncertainties, critical to many science and engineering applications, into modeling efforts presents an intractable computational burden for most real-world systems.
As a strategy for reducing the computational cost of such models while preserving high levels of fidelity in important components of the system, researchers have pursued projection-based reduced-order modeling—a technique that integrates ideas from data science, modeling, and simulation. Reduced-order modeling is a powerful tool that can enable real-time analysis and alleviate the computational burden posed by high-dimensional uncertainty quantification (UQ) problems.
The first step in building a reduced-order model (ROM) is to execute a set of analyses (such as running a full order model or FOM) during an offline ‘training’ stage. These analyses generate data that are used to extract important physical features, such as low-dimensional solution manifolds and interpolation points for approximating nonlinear functions. Next, the dimensionality and computational complexity of the high-fidelity model is reduced by projecting the governing equations onto a low-dimensional manifold and introducing other approximations where necessary. The resulting ROM can then be rapidly evaluated during an online ‘deployed’ stage, thereby enabling multi-query analyses such as UQ and optimization, as well as on-the-spot decision making and control.
Sandia’s continued investment in reduced-order modeling research has contributed to the Labs’ emergence as a leader in this growing field.
Sandia’s continued investment in reduced-order modeling research has contributed to the Labs’ emergence as a leader in this growing field. It has also led to the development of cutting-edge algorithms and the creation of agile and performance-portable software libraries, which have made possible the deployment of ROM technologies on mission-critical problems and applications.While advances have been made in reduced-order modeling during the past 15-20 years, there remain significant challenges in applying ROMs to complex mission-critical problems relevant to Sandia and the DOE. Sandia researchers are addressing these challenges through the development of novel model reduction methodologies that improve on existing methods and possess desirable mathematical properties such as stability and convergence. These methodologies borrow and adapt concepts from not only traditional numerical analysis/methods, but also from the up-and-coming fields of machine learning (ML) and artificial intelligence (AI).
Development of novel reduced-order modeling methodologies
By leveraging ideas from computational fluid dynamics (CFD) and numerical discretizations such as closure modeling and energy-based formulations, Sandia researchers have developed techniques that give rise to ROMs with improved stability properties, as well as ROM formulations that preserve the intrinsic structure of the underlying physical system (e.g., Lagrangian or Hamiltonian structure, mass/momentum/energy conservation). Space-time and windowed least-squares model reduction approaches originating at Sandia are based on well-established concepts in time-discretization and optimization, and have addressed several key deficiencies in existing model reduction techniques, including their dependence on time discretization, their potential for exhibiting exponential error growth in time, and their parallel efficiency limitations.
Recently, significant progress has been made towards overcoming a well-known limitation of predictive ROMs: if a solution feature was not observed during the training stage of the ROM, the ROM will be incapable of capturing the feature when deployed online and may therefore lack robustness. This problem can be remedied through an online basis adaptation algorithm known as “adaptive h-refinement for ROMs,” an approach developed at Sandia that is similar in flavor to adaptive mesh refinement (AMR).
In addition to improving ROM accuracy and robustness, Sandia’s research in ROM has led to the construction of ROMs that are more efficient for large-scale multi-scale/multi-physics systems through, for instance, the development of a domain-decomposition-based “divide and conquer” model reduction methodology for decomposable systems that allows subdomain/component ROMs to be assembled into a full-system ROM in arbitrary ways.
The rise of ML/AI has further motivated Sandia researchers to explore ways to integrate concepts from these fields into the field of model reduction. This resulted in the creation of a machine-learning-based framework for quantifying and modeling ROM errors, and, more recently, the introduction of a novel nonlinear deep convolutional autoencoder architecture within a classical projection-based ROM.
Advancing ROM through ML and AI
Nearly all model-reduction techniques employ a projection of the governing equations onto a linear subspace of the original state space. Unfortunately, restricting the state to evolve in a linear subspace imposes a fundamental limitation on the accuracy of the resulting ROM. In particular, linear-subspace ROMs are often inadequate when applied to problems exhibiting a slowly decaying Kolmogorov n-width, e.g., advection-dominated problems such as the high-speed, turbulent flow over an airfoil or re-entry vehicle.
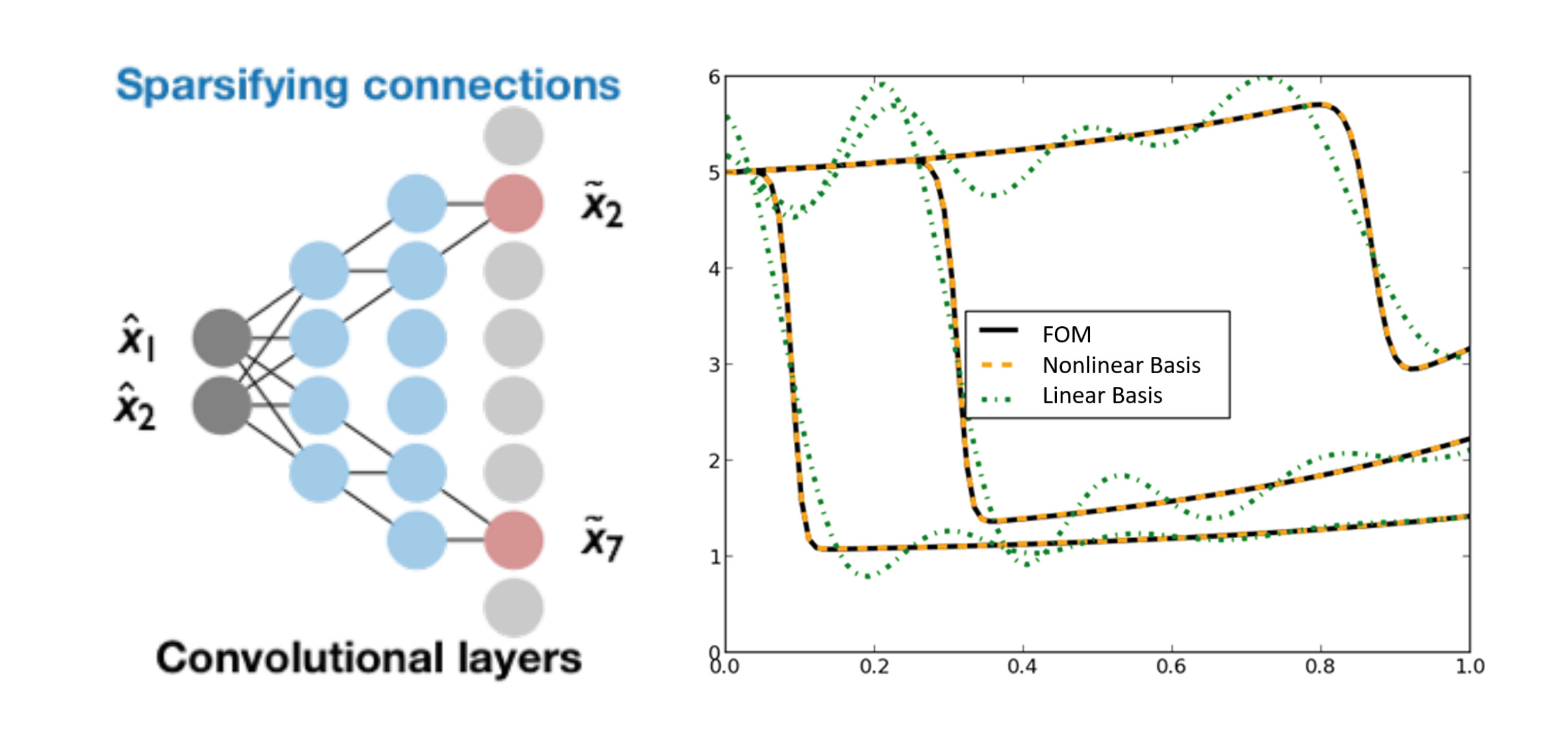
Figure 2. (right) The use of a nonlinear (autoencoder) basis results in an improvement in the solution accuracy for LSPG ROMs for the solution of the 1D Burgers equation.
To address this, Sandia researchers developed a novel framework that involves projecting dynamical systems onto nonlinear manifolds (see Figure 1). These manifolds are generated in a computationally tractable manner by employing advanced ML techniques, namely convolutional autoencoders. The accuracy of the resulting ROMs can be improved further through the introduction of structure preserving ROM formulations, originally developed for ROMs with linear subspaces. This novel ML application resulted in Sandia researchers developing ML techniques to meet the unique challenges of this space such as the new convolutional autoencoder architectures that are compatible with the unstructured spatial discretization schemes common in computational physics. The use of nonlinear manifold projection (autoencoders) has resulted in a significant improvement in solution accuracy over more well-established linear methods, such as Least-Squares Petrov-Galerkin (LSPG) projection (see Figure 2).