3.2.3. Radiation Transport Equation
For applications involving PMR, both the radiative heat flux and the divergence of the radiative heat flux are needed. The radiative heat flux vector provides the radiative flux to the boundary of the heat conduction region. The flux divergence provides one of the principal volumetric heat sources in the turbulent combustion region for fire applications.
3.2.3.1. Boltzmann Transport Equation
The spatial variation of the radiative intensity corresponding to
a given direction and at a given wavelength within a radiatively
participating material, , is governed by the Boltzmann transport
equation. In general, the Boltzmann equation represents a balance
between absorption, emission, out-scattering, and in-scattering of
radiation at a point. For combustion applications, however, the
steady form of the Boltzmann equation is appropriate since the
transient term only becomes important on nanosecond time scales
which is orders of magnitude shorter than the fastest chemical
reaction [7].
Experimental data shows that the radiative properties for
heavily sooting, fuel-rich hydrocarbon diffusion flames
(% to
% soot by volume) are dominated by
the soot phase and to a lesser extent by the gas phase
(Modest [8], pg. 425).
Since soot emits and absorbs radiation in a relatively constant
spectrum, it is common to ignore wavelength effects when modeling
radiative transport in these environments. Additionally, scattering
from soot particles commonly generated by hydrocarbon flames is
several orders of magnitude smaller that the absorption effect
and may be neglected [7]. With these assumptions
in mind, the appropriate form of the Boltzmann radiative transport
equation for heavily sooting hydrocarbon diffusion flames is
(3.62)
where is the absorption coefficient,
is the intensity
along the direction
, and
is the temperature.
The flux divergence (on the right hand side of (3.33)) may be written as a difference between the radiative emission and mean incident radiation at a point,
(3.63)
where is the scalar flux. The quantity,
, is often
referred to as the mean incident intensity [9].
The scalar flux and radiative flux vector represent angular moments of the directional radiative intensity at a point [8],
(3.64)
(3.65)
where and
are the zenith and azimuthal
angles respectively as shown in Ordinate Direction Definition, with
.
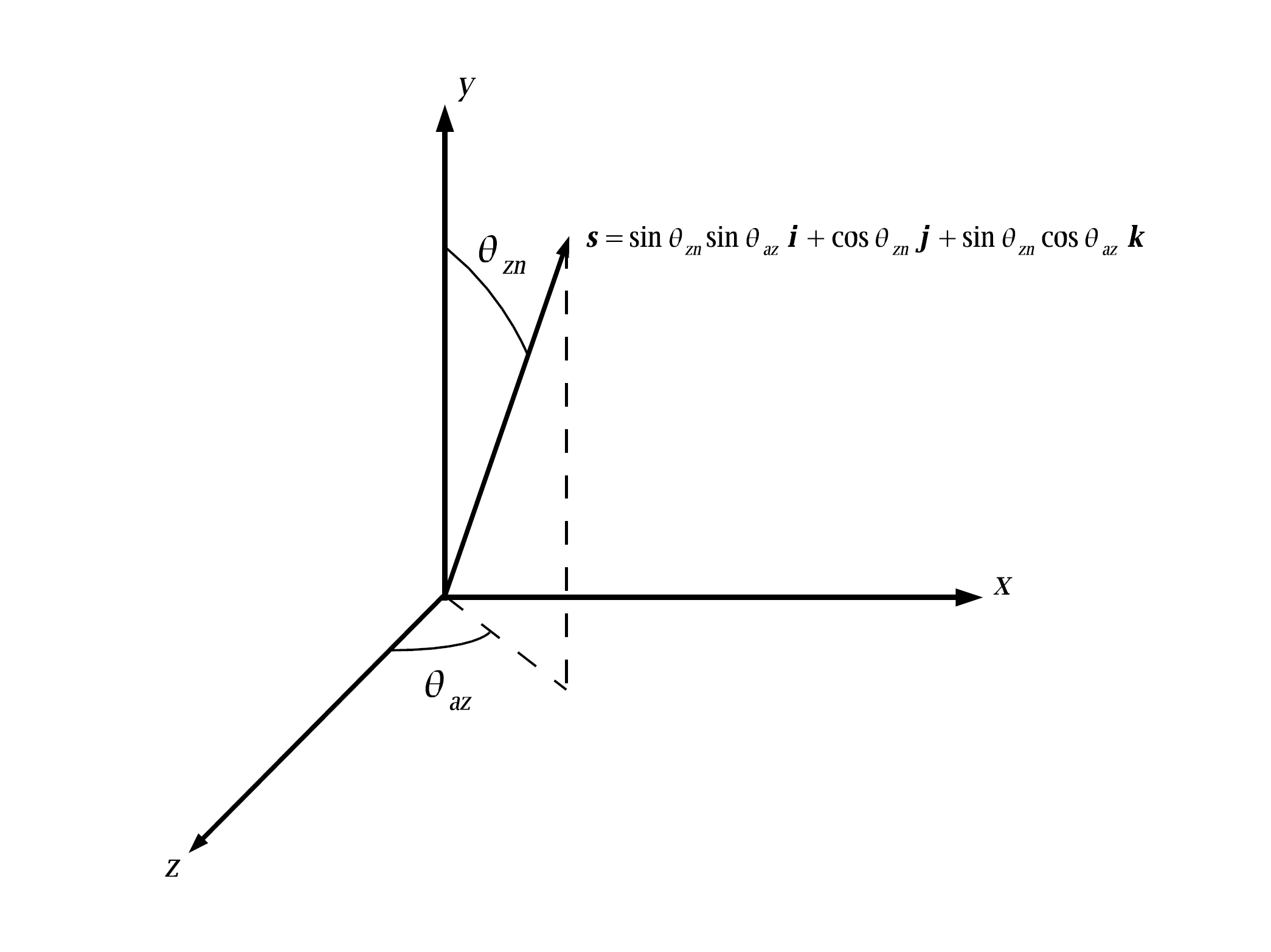
Fig. 3.1 Ordinate Direction Definition
3.2.3.2. Radiation Intensity Boundary Condition
The radiation intensity must be defined at all portions
of the boundary along which , where
is the
outward directed
unit normal vector at the surface. The intensity is applied as a
Dirichlet condition which must be determined from the surface
properties and temperature. The diffuse surface assumption
provides reasonable accuracy for many engineering combustion
applications. The intensity leaving a diffuse surface in all
directions is given by
(3.66)
where is the total normal emissivity of the
surface,
is the transmissivity of the surface,
is the
temperature of the boundary,
is the environmental
temperature and
is the incident radiation, or irradiation for
direction
. Recall that the relationship given by Kirchhoff’s
Law that relates emissivity, transmissivity and reflectivity,
, is
(3.67)
where it is implied that .