3.4. Numerics

We surveyed commercial codes that provide turbulent combustion capabilities and discovered that most of those codes are based on finite volume methods. Between commercial evidence and our own experiences, we came to the conclusion that finite volume methods would provide a robust and stable means of solving the fire math models. Our selection of finite volume methods is constrained by the current implementation of software architecture in the SIERRA Frameworks. The mesh must be unstructured with flow variables located at the element vertices. The domain boundary is coincident with element faces. The discrete equations are assembled on an element-by-element procedure using the SIERRA workset approach for cache-use efficiency. The finite volume approach that we implement is based on the control-volume finite-element method.

Control-volume finite-element methods (CVFEM) are a class of numerical methods for solving the Navier-Stokes equations of fluid mechanics. Although the methods are applicable to the most general case of a compressible flow, they are most commonly applied to incompressible flows. This text is a discussion of the control-volume finite-element methods appropriate for numerical solutions to the low-Mach number Navier-Stokes equations with heat and mass transfer—the equations used to describe physical applications such a combustion or chemical vapor deposition.

The CVFEM’s are a combination of desirable features from both the finite-element method (FEM) and the finite-volume method (FVM), though the CVFEM is truly a finite-volume method. The CVFEM differed from other FVM’s at its inception in that the CVFEM used non-staggered, unstructured meshes like a FEM. Concepts from the finite-element method include: 1) the finite-element data structure and the associated shape functions or interpolation functions, 2) integral equations assembled on an element-by-element basis, an efficient process for cache-based computer architectures, and 3) unstructured meshes with arbitrary connectivity (this is not particular to FEM’s, but certainly more common). Reviews for the finite-element method are given by Zienkiewicz and Taylor [127, 128], Tezduyar [66], and Gresho [129]. Concepts from the finite volume method include: 1) physically-based integral formulation constructed from physically-based interpolation functions, 2) conservation properties at the control-volume level, and 3) both a convecting and convected velocity field to avoid pressure-velocity decoupling. Some comprehensive reviews for the finite-volume method are given by Patankar [130], Shyy [131], and Ferziger and Peric [132]. An extensive literature review of control volume finite element methods (CVFEM) is given in Review of Control Volume Finite Element Methods.

The standard mesh configuration for vertex-centered CVFEM’s has all flow variables collocated at the grid points, also called nodes. The nodes are the vertices of the finite-elements, as shown in Figure 3.28. The finite-volumes, also called control volumes, are centered about the nodes. Each element contains a set of sub-faces that define control-volume surfaces. The sub-faces consist of the segments or surfaces that bisect the element faces.

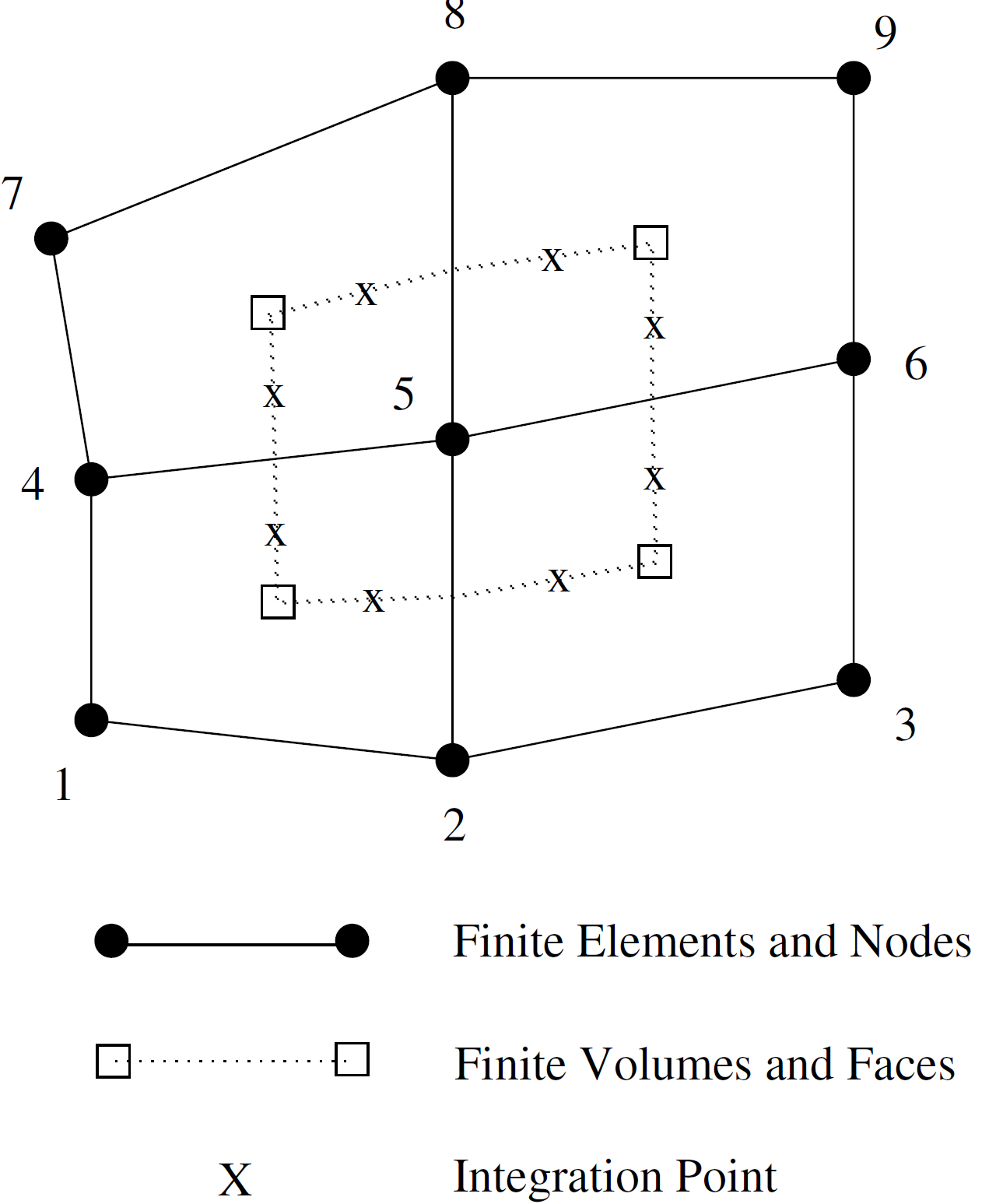
Fig. 3.28 Control Volume is Centered about Finite-Element Node