4.9.6. Advection Methods

Consider transport of an arbitrary scalar $\phi$ between the control volumes $C_0$ and $C_1$ in the figure below.

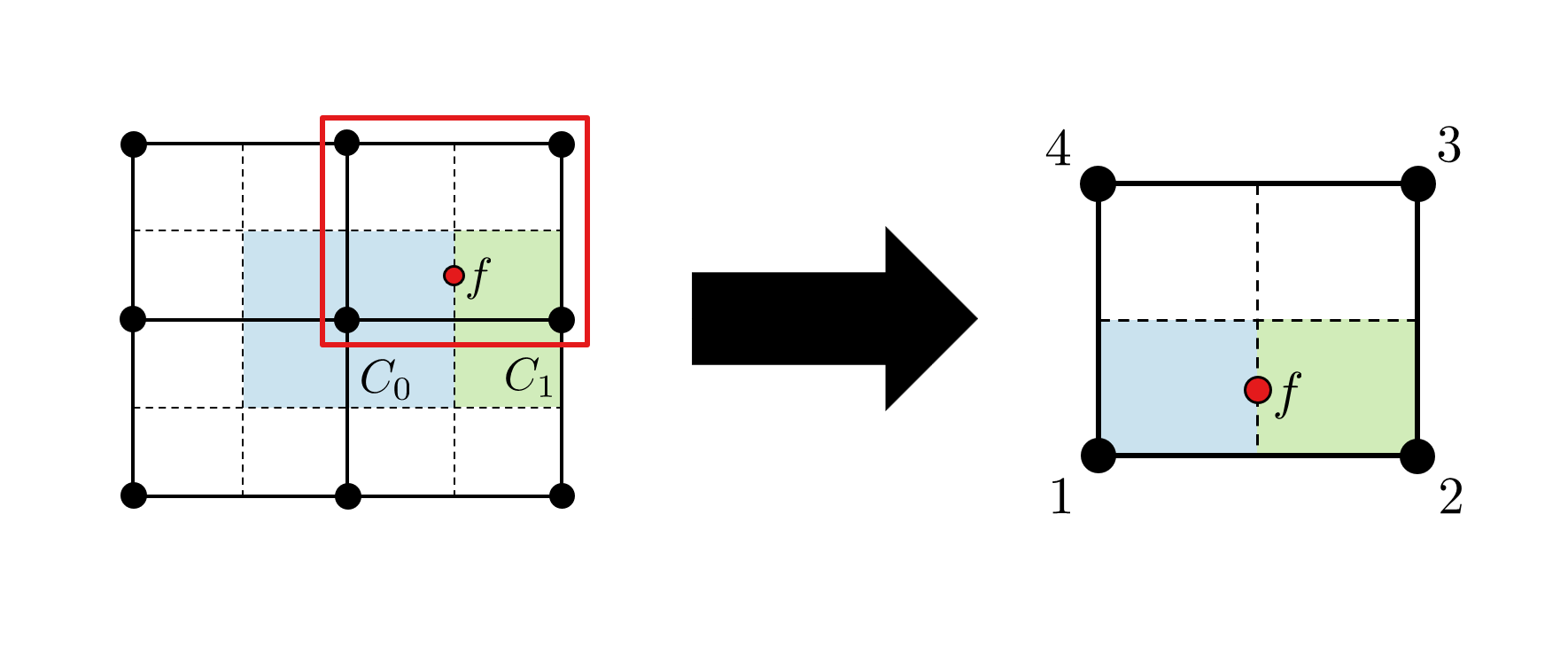
Advection control volumes — Fig. 4.2 Control volumes for flux across a single face f

In order to calculate the advection of $\phi$ we need to be able to evaluate $\dot{m}_f \phi_f$ . The mass flow rate through the face ( $\dot{m}_f$ ) is determined by our continuity solve, but for each transport scalar we need to determine $\phi_f$ . The scheme used to find $\phi_f$ can come in a number of different flavors. The basic ones are described in the following sections, followed by the blending scheme Fuego uses to combine them.

4.9.6.1. Central Difference

Using a central difference scheme (CDS) we simply interpolate $\phi$ from the node locations to the face location using the element weights $w_i$ , so

(4.13) $\phi_f^{\rm{CDS}} = \sum\limits_i w_i \phi_i$

This provides a second order accurate advection operator, but poor stability properties in regimes with high Peclet numbers.

4.9.6.2. Upwind Method

Using only the value of the upwind node from the face provides a simple, stable, inexpensive approach, but it is only first order accurate.

(4.14) $\phi_f^{\rm{UPW}} = \left( \begin{matrix} \phi_1 & \dot{m}_f > 0 \\ \phi_2 & \dot{m}_f < 0 \end{matrix} \right.$

4.9.6.3. MUSCL Upwind

Using MUSCL (Monotonic Upstream-centered Scheme for Conservation Laws) we use the gradient of $\phi$ at the upwind node to project a value of $\phi_f$ from the node location.

(4.15) $\phi_f^{\rm{MUSCL}} = \left( \begin{matrix} \phi_1 + \Phi(r_1) \left( \bf{r}_{1,f} \cdot \nabla \phi_1 \right) & \dot{m}_f > 0 \\ \phi_2 + \Phi(r_2) \left( \bf{r}_{2,f} \cdot \nabla \phi_2 \right) & \dot{m}_f < 0 \end{matrix} \right.$

where we also require a limiter function, $\Phi(r)$ that uses

(4.16) $r_1 = \frac{\phi_1 - \hat{\phi}_1}{\phi_2 - \phi_1}$

(4.17) $\hat{\phi}_1 = \phi_2 - 2 \nabla \phi_1 \cdot \left( \bf{x}_2 - \bf{x}_1 \right)$

4.9.6.4. Fuego Blending Approach

The cell Peclet number is the ratio of advection to diffusion, defined as

(4.18) $Pe = \frac{\bf{u} \cdot \delta \bf{x}}{\nu}$

Fuego uses several blending functions to combine the three advection operators as a function of cell Peclet number.

(4.19) $\phi_f = \eta \phi_f^{\rm{UPW}} + \left(1 - \eta \right) \left[ \chi \phi_f^{\rm{US}} + \left(1 - \chi \right) \phi_f^{\rm{CDS}} \right]$

Here, $\eta$ is the user-specified first order upwind factor (a value between 0 and 1), $\chi$ is a central difference blending coefficient that transitions between 0 and 1 depending on the cell Peclet number (described below), and $\phi_f^{\rm{US}}$ is the user-specified upwind choice, either $\phi_f^{\rm{UPW}}$ or $\phi_f^{\rm{MUSCL}}$ .

When you set $\eta$ , you define what fraction of the advection operator is always first-order upwind, and the remaining fraction is then split between your choice of upwind operator (UPW or MUSCL) and central-difference based on $\chi$ .

The blending coefficient is either defined by

(4.20) $\chi = \frac{\left(\zeta Pe \right)^2}{5 + \left(\zeta Pe \right)^2}$

where $\zeta$ is specified by HYBRID UPWIND FACTOR and can be any value greater than zero, or by

(4.21) $\chi = \frac{1}{2} \left[ 1 + \tanh \left( \frac{Pe - S}{W} \right)\right]$

where $S$ is defined by HYBRID UPWIND SHIFT and $W$ is defined by HYBRID UPWIND WIDTH.

These parameters can be set globally, or per equation. The per-equation specification takes precedence, so you can set a global configuration, and then override it only for certain equations.

Begin Solution Options
  Upwind Method = [UPW | MUSCL] # Default "UPW"
  First Order Upwind Factor = [0 to 1] # Default 0
  Hybrid Upwind Factor = [0+] # Default 1
  Upwind Limiter = [None, Superbee, Minmod, Van_Albada, Van_Leer] # Default "None"
  Hybrid Upwind Method = [Blending | Tanh] # Default "Blending"
  Hybrid Upwind Shift = X # Default 0
  Hybrid Upwind Width = X # Default 0

An example configuration below uses no first-order upwinding, and blends between MUSCL and CDS using the TANH blending rule with different transition points for momentum and the other equations.

Begin Solution Options
  UPWIND METHOD IS MUSCL
  UPWIND LIMITER IS VAN_LEER

  FIRST ORDER UPWIND FACTOR = 0.0  # 0% upwinding

  HYBRID UPWIND METHOD = TANH
  HYBRID UPWIND WIDTH = 2
  HYBRID UPWIND SHIFT = 2

  HYBRID UPWIND WIDTH = 200 FOR EQUATION X_Momentum
  HYBRID UPWIND WIDTH = 200 FOR EQUATION Y_Momentum

  HYBRID UPWIND SHIFT = 2000 FOR EQUATION X_Momentum
  HYBRID UPWIND SHIFT = 2000 FOR EQUATION Y_Momentum