5.2. Material Models

This section contains descriptions of the general fully supported materials available in Sierra/SM. Additional models relevant to shock problems are described in the separate Sierra/SM ITAR User’s Guide: Addendum for Shock Capabilities. Also, additional experimental, in-development, and specialty models may be found in the Sierra/SM Capabilities in Development manual.

5.2.1. Elastic Model

BEGIN PARAMETERS FOR MODEL ELASTIC
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
END [PARAMETERS FOR MODEL ELASTIC]

The elastic model is a hypoelastic extension of isotropic, small-strain, linear elasticity [[1], [2], [3]]. The stress-strain response for an isotropic, elastic material is

\[\sigma_{ij} = \lambda\delta_{ij}\varepsilon_{kk} + 2\mu\varepsilon_{ij}\]

where the Lamé constants, \(\lambda\) and \(\mu\), are given by

\[\lambda = \frac{E\nu}{\left( 1+\nu \right)\left( 1-2\nu \right)} \;\;\; ; \;\;\; \mu = \frac{E}{2\left( 1+\nu \right)}\]

This model is extended to a finite-deformation, hypoelastic model by first making it a rate equation. Then the stress rate is replaced with an objective stress rate and the strain rate is replaced with the rate of deformation. This gives us

\[\stackrel{\circ}{\sigma}_{ij} = \lambda\delta_{ij}D_{kk} + 2\mu D_{ij}\]

The stress rate is arbitrary, as long as it is objective. Two objective stress rates are commonly used: the Jaumann rate and the Green-McInnis rate. For problems with fixed principal axes of deformation, these two rates give the same answers. For problems where the principal axes of deformation rotate during the deformation, the two rates can give different answers. Generally speaking there is no reason to pick one objective rate over another. Sierra/SM uses the Green-McInnis rate.

The fourth-order elastic moduli are used in many constitutive models. There are many equivalent representations for the elastic moduli. In index notation we present the following three representations

\[\stackrel{\circ}{\sigma}_{ij} = \mathbb{C}_{ijkl}D_{kl} \nonumber\]
\[\begin{split}\mathbb{C}_{ijkl} & = \frac{E}{1+\nu} \left[ \frac{\nu}{1-2\nu}\delta_{ij}\delta_{kl} + \frac{1}{2} \left( \delta_{ik}\delta_{jl} + \delta_{il}\delta_{jk} \right) \right] \\ \nonumber \\ \mathbb{C}_{ijkl} & = \lambda \delta_{ij}\delta_{kl} + \mu \left( \delta_{ik}\delta_{jl} + \delta_{il}\delta_{jk} \right) \\ \nonumber \\ \mathbb{C}_{ijkl} & = K \delta_{ij}\delta_{kl} + \mu \left( \delta_{ik}\delta_{jl} + \delta_{il}\delta_{jk} - \frac{2}{3} \delta_{ij}\delta_{kl} \right)\end{split}\]

where \(K\) is the elastic bulk modulus and is given by

\[K = \frac{E}{3\left( 1-2\nu \right)}\]

See Section 5.1.5 for more information on elastic constants input.

There are no output variables available for the elastic model. For information about the elastic model, consult [[4]].

5.2.2. Thermoelastic Model

BEGIN PARAMETERS FOR MODEL THERMOELASTIC
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Thermoelastic functions
  #
  YOUNGS MODULUS FUNCTION = <string> ym_function_name
  POISSONS RATIO FUNCTION = <string> pr_function_name
END [PARAMETERS FOR MODEL THERMOELASTIC]

The thermoelastic material model is used to describe a temperature-dependent linear elastic material. This is a hypoelastic model generally valid for small strains.

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input.

  • The YOUNGS MODULUS FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope. The function defines a scale factor on Young’s modulus as a function of temperature.

  • The POISSONS RATIO FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope. The function defines a scale factor on Poisson’s ratio as a function of temperature.

For information about the thermoelastic model, consult [[4]]. Several plasticity models share the same underlying implementation. Output state variables available for this model are listed in Table 5.9. Note, depending on options used (temperature dependence of properties, failure, etc.) some of these state variables may not be computed.

5.2.3. Neo-Hookean Model

BEGIN PARAMETERS FOR MODEL NEO_HOOKEAN
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
END [PARAMETERS FOR MODEL NEO_HOOKEAN]

The neo-Hookean model is a hyperelastic generalization of isotropic, small-strain linear elasticity. The stress-strain response for the neo-Hookean model may be determined from a free energy function - in this case the strain energy density, \(W\). The form of the strain energy density ([[5]]) is

(5.1)\[W(C_{ij}) = \frac{1}{2}K\left[\frac{1}{2}\left( J^{2}-1 \right) - \ln J \right] + \frac{1}{2}\mu\left( \bar{C}_{kk} - 3 \right) \;\;\; ,\]

where \(K\) and \(\mu\) are the bulk and shear moduli, respectively. The deformation measure is given by \(C_{ij}\), the components of the right Cauchy-Green tensor, where \(C_{ij} = F_{ki}F_{kj}\). The determinant of the deformation gradient is given by \(J\) and is a measure of the volumetric part of the deformation. \(\bar{C}_{ij}\) provides the isochoric part of the deformation and is given by

(5.2)\[\bar{C}_{ij} = \bar{F}_{ki}\bar{F}_{kj}, \;\;\; ; \;\;\; \bar{F}_{ij} = J^{-1/3}F_{ij} \;\;\; .\]

The second Piola-Kirchoff stress, with components \(S_{ij}\), may be determined by taking a derivative of the strain energy density and the Cauchy stress may be found by mapping from the second Piola-Kirchoff stress. The components of the Cauchy stress are

(5.3)\[\sigma_{ij} = \frac{1}{2}K \left( J - \frac{1}{J} \right) \delta_{ij} + J^{-5/3}\mu\left( B_{ij} - \frac{1}{3}B_{kk}\delta_{ij} \right) \;\;\; ,\]

where \(B_{ij} = F_{ik}F_{jk}\), are the components of the left Cauchy-Green tensor and \(\delta_{ij}\) is the Kronecker delta.

Linearizing (5.3) we recover small strain linear elasticity

(5.4)\[\begin{split}\sigma_{ij} & = \left( K - \frac{2}{3}\mu \right) u_{k,k} \delta_{ij} + \mu \left( u_{i,j} + u_{j,i} \right) \nonumber \\ & \\ & = \left( K - \frac{2}{3}\mu \right) \varepsilon_{kk} \delta_{ij} + 2\mu \varepsilon_{ij} \nonumber \;\;\; .\end{split}\]

The neo-Hookean model is used for the recoverable (elastic) part for a number of inelastic, finite deformation constitutive models.

There are no output variables available for the neo-Hookean model.

5.2.4. Elastic Fracture Model

BEGIN PARAMETERS FOR MODEL ELASTIC_FRACTURE
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Fracture parameters
  #
  MAX STRESS                    = <real>
  CRITICAL CRACK OPENING STRAIN = <real>
END [PARAMETERS FOR MODEL ELASTIC_FRACTURE]

The elastic fracture model is linear elastic model with a simple failure model using a maximum-principal-stress failure criterion. Post failure, the stress decays isotropically based on additional strain parallel to the maximum principal stress. The critical crack opening strain, \(\varepsilon_{ccos}\) is the value of the component of strain over which the stress is decayed to zero. This strain parameter can be adjusted so that failure is mesh independent.

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input.

  • The maximum principal stress at which failure occurs is defined with the MAX STRESS command line.

  • The component of strain over which the stress decays to zero is defined with the CRITICAL CRACK OPENING STRAIN command line. This component of strain is aligned with the maximum-principal-stress direction at failure.

Output variables available for this model are listed in Table Table 5.1.

Table 5.1 State Variables for ELASTIC FRACTURE Model (Section 5.2.4)

Name

Variable Description

CRACK_OPENING_STRAIN

Critical value of opening strain

FAILURE_DIRECTION

Crack opening direction - vector

FAILURE_DIRECTION_X

Crack opening direction - x component

FAILURE_DIRECTION_Y

Crack opening direction - y component

FAILURE_DIRECTION_Z

Crack opening direction - z component

PRINCIPAL_STRESS

Value of maximum principal stress

MAX_RADIUS

Von Mises stress at failure

MAX_PRESS

Stress tensor pressure at failure

MAX_STRESS

Maximum principal stress (UQ)

CRITICAL_CRACK_OPENING_STRAIN

Critical crack opening strain (UQ)

5.2.5. Elastic-Plastic Model

BEGIN PARAMETERS FOR MODEL ELASTIC_PLASTIC
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Hardening Behavior
  #
  YIELD STRESS      = <real>
  BETA              = <real> (1.0)
  HARDENING MODULUS = <real>
END [PARAMETERS FOR MODEL ELASTIC_PLASTIC]

The elastic-plastic model is a hypoelastic, rate-independent linear hardening plasticity model. The rate form of the constitutive equation assumes an additive split of the rate of deformation into an elastic and plastic part

(5.5)\[D_{ij} = D^{\text{e}}_{ij} + D^{\text{p}}_{ij}\]

The stress rate only depends on the elastic strain rate in the problem

(5.6)\[\stackrel{\circ}{\sigma}_{ij} = \mathbb{C}_{ijkl}D^{\text{e}}_{kl}\]

where \(\mathbb{C}_{ijkl}\) are the components of the fourth-order, isotropic elasticity tensor.

The key to the model is finding the plastic rate of deformation. For associated flow the plastic rate of deformation is in a direction normal to the yield surface. The yield surface is given by

(5.7)\[f\left(\sigma_{ij},\alpha_{ij},\bar{\varepsilon}^{p}\right) = \phi\left(\sigma_{ij},\alpha_{ij}\right) - \bar{\sigma}\left(\bar{\varepsilon}^{p}\right) = 0\]

where \(\phi\) is the effective stress, \(\alpha_{ij}\) are the components of the back stress (used with kinematic hardening), and \(\bar{\sigma}\) is the hardening function which is a function of an internal state variable, the equivalent plastic strain \(\bar{\varepsilon}^{p}\). An example of such a yield surface (plotted in the deviatoric \(\pi\)-plane) is presented below in Fig. 5.4. The isotropy of the yield surface is clearly evident.

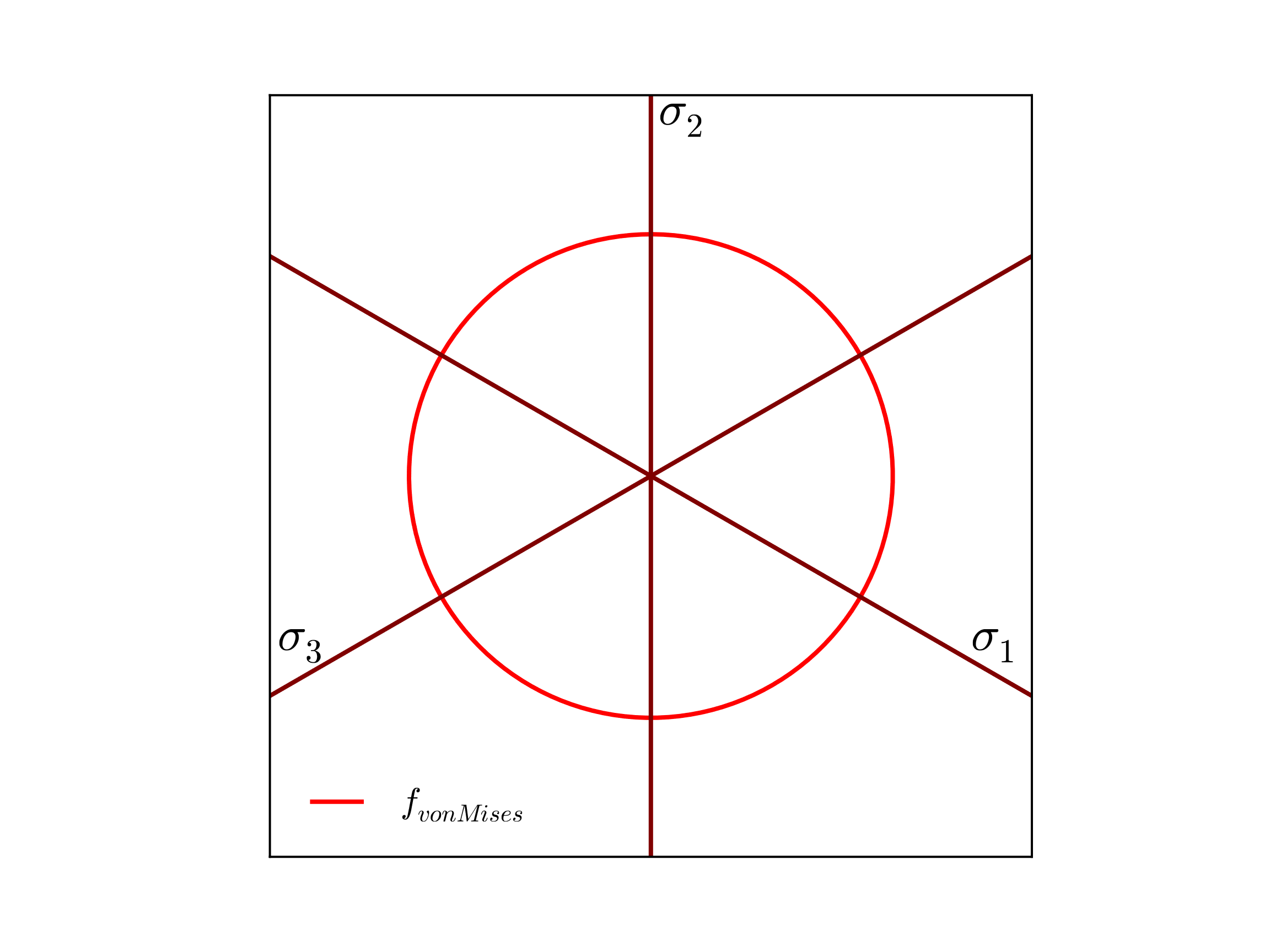
../../_images/vonMisesSurface.png

Fig. 5.4 Example von Mises yield surface (\(J_2\)) used by the elastic-plastic model presented in the deviatoric \(\pi\)-plane. In this case the surface is plotted for \(\alpha_{ij}=0\) and \(\bar{\varepsilon}^p=0\).

For the elastic plastic model a linear hardening law is assumed

(5.8)\[\bar{\sigma} = \sigma_{y} + H^{\prime}\bar{\varepsilon}^{p}\]

where \(\sigma_{y}\) is the yield stress and \(H^{\prime}\) is the hardening modulus. If the stress state is such that \(f < 0\), the the behavior of the material is elastic; if the stress state is such that \(f = 0\) and \(\dot{f} < 0\), i.e. the strain rate brings the stress inside the yield surface, then the behavior of the material is elastic; if the stress state is such that \(f = 0\) and \(\dot{f} > 0\), i.e. the strain rate brings the stress outside the yield surface, then plastic deformation occurs.

We assume associated flow in this model, which gives the plastic rate of deformation

(5.9)\[D^{\text{p}}_{ij} = \dot{\gamma}\frac{\partial\phi}{\partial\sigma_{ij}}\]

where \(\dot{\gamma}\) is the consistency parameter. For the elastic-plastic model the yield surface is assumed to be a von Mises yield surface with a back stress tensor to denote the center of the yield surface. The effective stress for a von Mises yield surface is

(5.10)\[\phi\left(\sigma_{ij}\right) = \sqrt{\frac{3}{2}\xi_{ij}\xi_{ij}} \;\;\; ; \;\;\; \xi_{ij} = s_{ij} - \alpha_{ij}\]

where \(s_{ij}\) are the components of the deviatoric stress tensor

(5.11)\[s_{ij} = \sigma_{ij} - \frac{1}{3}\delta_{ij}\sigma_{kk}\]

and \(\alpha_{ij}\) are the components of the back stress tensor, another internal state variable.

The equivalent plastic strain is found through equating the rate of plastic work

(5.12)\[\begin{split}\dot{W}^{p} = \sigma_{ij}D^{\text{p}}_{ij} = \bar{\sigma}\dot{\bar\varepsilon}^{p} \;\;\; \rightarrow \;\;\; \dot{\bar\varepsilon}^{p} = \dot{\gamma} \nonumber \\ \bar{\varepsilon}^{p} = \int_{0}^{t} \dot{\gamma} dt \nonumber\end{split}\]

Finally, the model allows for kinematic hardening through the back stress. The back stress is a symmetric, deviatoric rank two tensor that evolves in the following manner

(5.13)\[\dot{\alpha}_{ij} = \frac{2}{3}\left( 1-\beta \right) H^{\prime} D_{ij}^{\text{p}}\]

The radius of the yield surface can be defined, \(R = \sqrt{\xi_{ij}\xi_{ij}}\). The evolution of the radius of the yield surface is given by

(5.14)\[\dot{R} = \sqrt{\frac{2}{3}} \beta H^{\prime} \dot{\bar\varepsilon}^{p}\]

In (5.13) and (5.14) the parameter \(\beta \in [0,1]\) distributes the hardening between isotropic and kinematic hardening. If \(\beta = 1\) the hardening is isotropic, if \(\beta = 0\) the hardening is kinematic, and if \(\beta\) is between 0 and 1 the hardening is a combination of isotropic and kinematic. In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input. The elastic constants describe both the pre-yield behavior of the model and the slope of post yield unloading.

  • The yield stress, the stress at which yield first initiates, is defined with the YIELD STRESS command line.

  • The hardening modulus, the slope of the post yield hardening curve, is defined with the HARDENING MODULUS command line.

  • The beta parameter defines if hardening is isotropic or kinematic. See Section 5.1.6 for details on the beta parameter.

Output variables available for this model are listed in Table 5.2 and Table 5.3. For information about the elastic-plastic model, consult [[4]].

Table 5.2 State Variables for ELASTIC PLASTIC Model (Section 5.2.5)

Name

Description

EQPS

equivalent plastic strain, \(\bar{\varepsilon}^{p}\)

RADIUS

radius of the yield surface, \(R\)

BACK_STRESS

back stress (symmetric tensor), \(\alpha_{ij}\)
Table 5.3 State Variables for ELASTIC PLASTIC Model for Shells (Section 5.2.5)

Name

Description

EQPS

equivalent plastic strain, \(\bar{\varepsilon}^{p}\)

TENSILE_EQPS

equivalent plastic strain only accumulated when the material is in tension (trace of stress tensor is positive)

RADIUS

radius of the yield surface, \(R\)

BACK_STRESS

back stress (symmetric tensor), \(\alpha_{ij}\)

ITERATIONS

radial return iterations

ERROR

error in plane stress iterations

PS_ITER

plane stress iterations

TSTRAIN

integrated thickness strain

5.2.6. Elastic-Plastic Power-Law Hardening Model

BEGIN PARAMETERS FOR MODEL EP_POWER_HARD
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Hardening behavior
  #
  YIELD STRESS       = <real>
  HARDENING CONSTANT = <real>
  HARDENING EXPONENT = <real>
  LUDERS STRAIN      = <real>
END [PARAMETERS FOR MODEL EP_POWER_HARD]

The elastic-plastic power law hardening model is a hypoelastic, rate-independent plasticity model with power law hardening [[6]]. The rate form of the constitutive equation assumes an additive split of the rate of deformation into an elastic and plastic part

\[D_{ij} = D^{\text{e}}_{ij} + D^{\text{p}}_{ij}\]

The stress rate only depends on the elastic strain rate in the problem

\[\stackrel{\circ}{\sigma}_{ij} = \mathbb{C}_{ijkl}D^{\text{e}}_{kl}\]

where \(\mathbb{C}_{ijkl}\) are the components of the fourth-order, isotropic elasticity tensor.

The key to integrating the model is finding the plastic rate of deformation. For associated flow the plastic rate of deformation is in a direction normal to the yield surface. The yield surface is given by

(5.15)\[f\left( \sigma_{ij},\bar{\varepsilon}^{p} \right) = \phi\left(\sigma_{ij}\right) - \bar{\sigma} \left( \bar{\varepsilon}^{p} \right) = 0\]

where \(\phi\) is the equivalent stress and \(\bar{\sigma}\) is the hardening function which is a function of the equivalent plastic strain \(\bar{\varepsilon}^{p}\). For this model the hardening function uses a power law

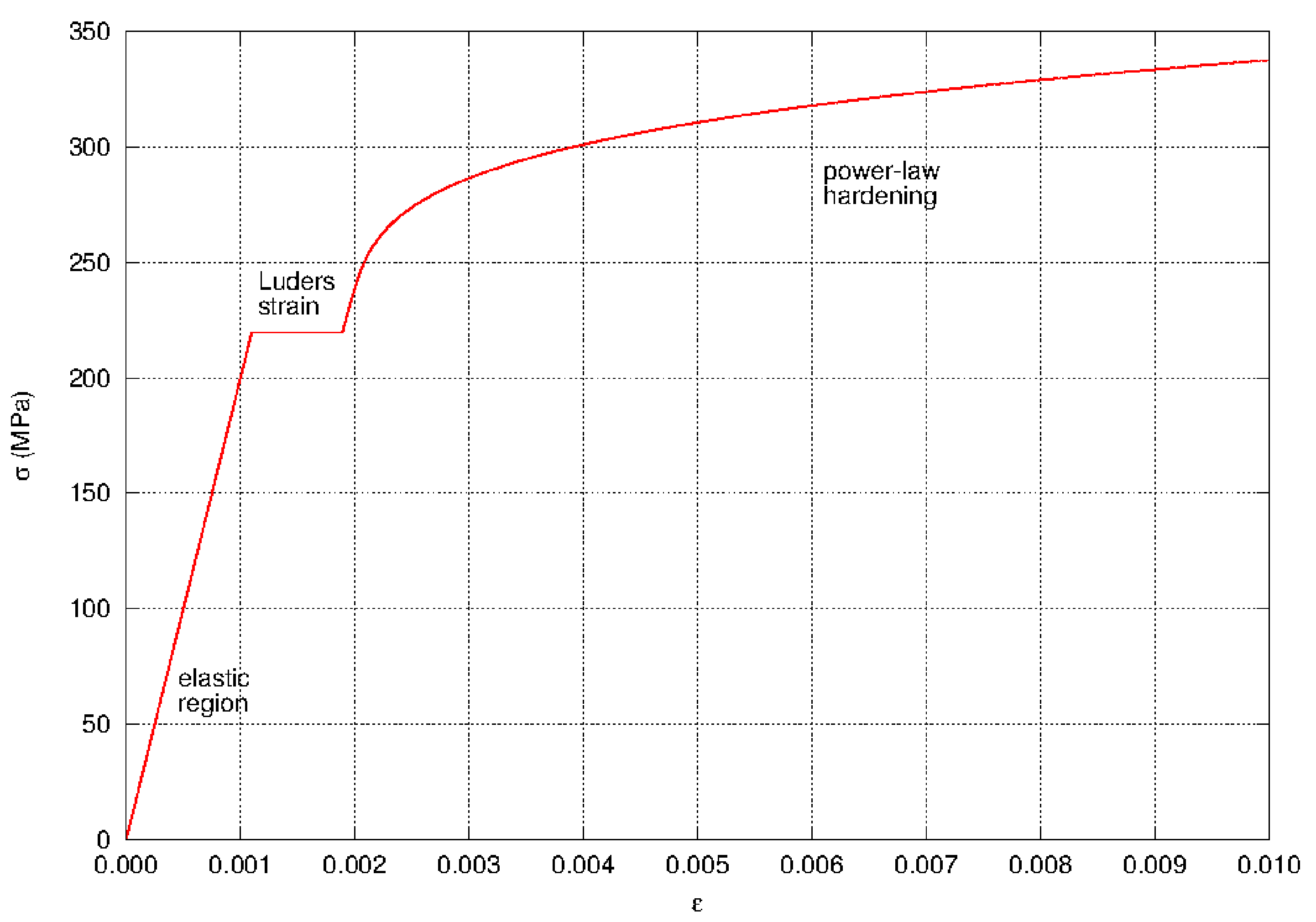
../../_images/ep_power_law.png

Fig. 5.5 Typical stress-strain response for the power-law hardening model.

\[\bar{\sigma} \left( \bar{\varepsilon}^{p} \right) = \sigma_{y} + A \left< \bar{\varepsilon}^{p} -\varepsilon_{L} \right>^{n}\]

which is shown in Fig. 5.5. The yield stress is \(\sigma_{y}\), the hardening constant is \(A\), the hardening exponent is \(n\), and the L"{u}ders strain is \(\varepsilon_{L}\). The bracket \(<\cdot>\) is the Macaulay bracket defined as

\[\begin{split}\left< x \right> = \begin{cases} 0,& \text{if } x \leq 0 \\ x,& \text{if } x > 0. \end{cases}\end{split}\]

By assuming associated plastic flow, the plastic rate of deformation can be written as

(5.16)\[D^{\text{p}}_{ij} = \dot{\gamma}\frac{\partial\phi}{\partial\sigma_{ij}}.\]

For this model the yield surface is chosen to be a von Mises yield surface, so

\[\phi\left(\sigma_{ij}\right) = \sqrt{\frac{3}{2}s_{ij}s_{ij}}\]

where \(s_{ij}\) are the components of the deviatoric stress

\[s_{ij} = \sigma_{ij} - \frac{1}{3}\delta_{ij}\sigma_{kk}\]

Unlike the elastic-plastic model Section 5.2.5, the power-law hardening model does not allow for kinematic hardening, so there is no back stress.

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input.

  • The YIELD STRESS is the stress at which the plastic power law yielding and hardening model takes effect. See Fig. 5.5.

  • The LUDERS STRAIN defines a regime of zero hardening modulus prior to onset of the power law hardening. A small Luder band is seen in the hardening behavior or many metals. See Fig. 5.5 for details.

  • The HARDENING CONSTANT command line and HARDENING EXPONENT command define the power law hardening curve. Past the Luder strain the hardened yield surface radius is given by the HARDENING CONSTANT times plastic strain to the HARDENING EXPONENT power.

Output variables available for this model are listed in Table 5.4 and Table 5.5. For information about the elastic-plastic power-law hardening model, consult [[4]].

Table 5.4 State Variables for EP POWER HARD Model (Section 5.2.6)

Name

Description

EQPS

equivalent plastic strain, \(\bar{\varepsilon}^{p}\)

TENSILE_EQPS

equivalent plastic strain only accumulated when the material is in tension (trace of stress tensor is positive)

RADIUS

radius of yield surface, \(R\)

ITERATIONS

number of radial return iterations
Table 5.5 State Variables for EP POWER HARD Model for Shells (Section 5.2.6)

Name

Description

EQPS

equivalent plastic strain, \(\bar{\varepsilon}^{p}\)

TENSILE_EQPS

equivalent plastic strain only accumulated when the material is in tension (trace of stress tensor is positive)

RADIUS

radius of yield surface, \(R\)

ITERATIONS

number of radial return iterations

ERROR

error in plane stress iterations

PS_ITER

plane stress iterations

5.2.7. Ductile Fracture Model

BEGIN PARAMETERS FOR MODEL DUCTILE_FRACTURE
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Yield surface parameters
  #
  YIELD STRESS       = <real>
  HARDENING CONSTANT = <real>
  HARDENING EXPONENT = <real>
  LUDERS STRAIN      = <real>
  #
  # Failure parameters
  #
  CRITICAL TEARING PARAMETER    = <real>
  CRITICAL CRACK OPENING STRAIN = <real>
END [PARAMETERS FOR MODEL DUCTILE_FRACTURE]

The ductile fracture model is identical to the elastic-plastic power-law hardening model with the addition of a failure criterion and an isotropic decay of the stress to zero during the failure process within the constitutive model. To accomplish this task, the tearing parameter, \(t_p\), proposed by Wellman [[7]] is introduced and the functional form as given as

(5.17)\[t_{p} = \int_0^{\varepsilon} {\Big\langle \frac{{2\sigma_{\max}}}{{3\left( {\sigma_{\max} - \sigma_{m} } \right)}}\Big\rangle } ^4 d\bar{\varepsilon}^{p}\]

where \(\sigma_{\max }\) is the maximum principal stress, and \(\sigma _{m}\) is the mean stress. It can also be noted that the tearing parameter evolves during the plastic deformation regime as indicated by integrating over the effective plastic strain, \(\bar{\varepsilon}^{p}\). The angle brackets denoting the Macaulay brackets, where

\[\begin{split}\langle x \rangle = \begin{cases} 0 \;\;\; \text{if } x \leq 0 \\ x \;\;\; \text{if } x > 0 \end{cases},\end{split}\]

are used to ensure that the failure process occurs only with tensile stress states and prevent “damage healing”. The failure process then initiates at a critical tearing parameter, \(t_p^{\text{crit}}\), and the corresponding stress decay occurs over a strain interval corresponding to the critical crack opening strain, \(\varepsilon_{\text{ccos}}\). Importantly, the \(\varepsilon_{\text{ccos}}\) serves a dual role in that it may also be used to control the energy dissipated during failure. With respect to the latter point, careful selection of the critical crack opening strain may be used to ensure consistent energy is dissipated through different meshes. This decay process is isotropic and linear with the current damage value being equivalent to the ratio of crack opening strain in the direction of the maximum principal stress to the critical value.

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input.

  • The YIELD STRESS is the stress at which the plastic power load yielding and hardening model takes effect. See Fig. 5.5.

  • The LUDERS STRAIN defines a regime of zero hardening modulus prior to onset of the power law hardening. A small Luder band is seen in the hardening behavior or many metals. See Fig. 5.5 for details.

  • The HARDENING CONSTANT command line and HARDENING EXPONENT command define the power law hardening curve. Past the Luder strain the hardened yield surface radius is given by the HARDENING CONSTANT times plastic strain to the HARDENING EXPONENT power.

  • CRITICAL TEARING PARAMETER defines the \(t_{p}\) value at which fracture and subsequent decay of stress will occur.

  • When the model undergoes additionally strain after reaching the critical tearing parameter the stress in the model will decay to zero. The amount strain over which the stress decays to zero is defined with the CRITICAL CRACK OPENING STRAIN command line. The relevant opening strain is the component of strain that is aligned with the maximum-principal-stress direction at initial failure.

Output variables available for this model are listed in Table 5.6. For information about the ductile fracture material model, consult [[7]].

Table 5.6 State Variables for DUCTILE FRACTURE Model (Section 5.2.7)

Name

Description

EQPS

equivalent plastic strain, \(\bar{\varepsilon}^{p}\)

RADIUS

radius of yield surface, \(R\)

BACK_STRESS

back stress - tensor \(\alpha_{ij}\)

TEARING_PARAMETER

Current value of the integrated tearing parameter

CRACK_OPENING_STRAIN

Current value of the crack opening strain. Will be zero prior to reaching the maximum tearing parameter.

FAILURE_DIRECTION

Crack opening direction (maximum principal stress direction at failure) - vector

DF_STRAIN_XX

XX component of current strain

DF_STRAIN_YY

YY component of current strain

DF_STRAIN_ZZ

ZZ component of current strain

DF_STRAIN_XY

XY component of current strain

DF_STRAIN_YZ

YZ component of current strain

DF_STRAIN_ZX

ZX component of current strain

MAX_RADIUS

Yield surface radius at failure

MAX_PRESS

Stress pressure norm at failure

5.2.8. Multilinear Elastic-Plastic Hardening Model

BEGIN PARAMETERS FOR MODEL MULTILINEAR_EP
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Hardening behavior
  #
  YIELD STRESS       = <real>
  BETA               = <real> (1.0)
  HARDENING FUNCTION = <string> hardening_function_name
  #
  # Functions
  #
  YOUNGS MODULUS FUNCTION = <string> ym_function_name
  POISSONS RATIO FUNCTION = <string> pr_function_name
  YIELD STRESS FUNCTION   = <string> yield_stress_function_name
END [PARAMETERS FOR MODEL MULTILINEAR_EP]

The multilinear elastic-plastic model is a generalization of the standard rate independent plasticity models already presented - the linear and power law hardening models. However, rather than having a specific functional form, the multilinear hardening model allows the user to input a piecewise linear function for the hardening curve. The rate form of the constitutive equation assumes an additive split of the rate of deformation into an elastic and plastic part such that

\[D_{ij} = D^{\text{e}}_{ij} + D^{\text{p}}_{ij}.\]

The stress rate only depends on the elastic strain rate so that,

\[\stackrel{\circ}{\sigma}_{ij} = \mathbb{C}_{ijkl}D^{\text{e}}_{kl},\]

where \(\mathbb{C}_{ijkl}\) are the components of the fourth-order, isotropic elasticity tensor.

The key to the model is finding the plastic rate of deformation. For associated flow, the plastic rate of deformation is in the direction normal to the yield surface. With a yield surface given by

\[\phi\left(\sigma_{ij}\right) - \bar{\sigma}\left(\bar{\varepsilon}^p\right) = 0\]

then the plastic rate of deformation can be written as

(5.18)\[D^{\text{p}}_{ij} = \dot{\gamma}\frac{\partial\phi}{\partial\sigma_{ij}}.\]

For this model the yield surface is taken to be a von Mises yield surface, such that

\[\phi\left(\sigma_{ij}\right) = \sqrt{\frac{3}{2}s_{ij}s_{ij}}\]

where \(s_{ij}\) are the components of the deviatoric stress

\[s_{ij} = \sigma_{ij} - \frac{1}{3}\delta_{ij}\sigma_{kk}.\]

For simplicity it is easier to write (5.18) in terms of the normal to the yield surface

\[D^{\text{p}}_{ij} = \dot{\gamma} N_{ij} \;\;\; ; \;\;\; N_{ij} = \frac{\partial\phi}{\partial\sigma_{ij}}/\left\|\frac{\partial\phi}{\partial\sigma_{ij}}\right\|\]

The model also incorporates temperature dependence in that the elastic properties and the yield stress can be functions of temperature. This is not as general as having the yield curves depend on temperature. For that behavior the thermoelastic-plastic model can be used.

An example stress vs. plastic strain hardening curve is shown in Fig. 5.6. This curve was generated for a loading case of uniaxial strain. In this case, the effective stress is the same as the uniaxial. Therefore, for use with the multilinear elastic-plastic model this curve would simply have to be discretized and used as input.

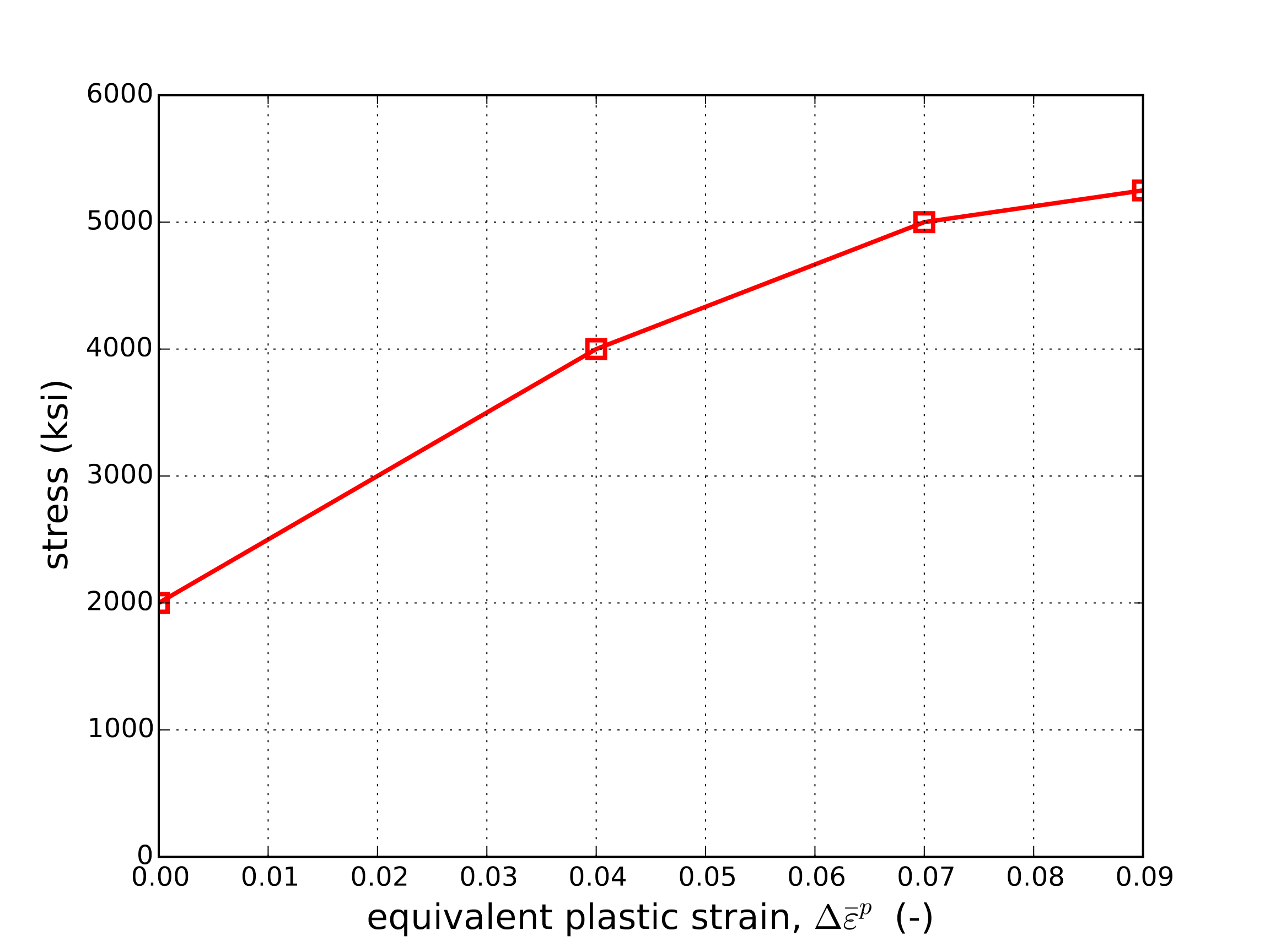
../../_images/mlep.png

Fig. 5.6 An example of a multilinear elastic-plastic stress-strain curve.

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input.

  • The beta parameter defines if hardening is isotropic or kinematic. See Section 5.1.6 for details on the beta parameter.

  • YIELD STRESS defines the stress where plastic yielding first occurs.

  • The HARDENING FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope. The function describes the hardening behavior of the material as stress versus equivalent plastic strain. The x values of the function should be values of equivalent plastic strain while the y values of the function can be either the increment of stress over the yield stress or the actual stress at the corresponding equivalent plastic strain. Note the hardening function can have its first point defined at (0,0), or at (0, YIELD_STRESS). Either function definition behaves the same as only the slope of the hardening function between two strains is used by the model.

  • The YOUNGS MODULUS FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on Young’s modulus as a function of temperature.

  • The POISSONS RATIO FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on Poisson’s ratio as a function of temperature.

  • The YIELD STRESS FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on the yield stress as a function of temperature.

Output variables available for this model are listed in Table 5.7 and Table 5.8.

Table 5.7 State Variables for MULTILINEAR EP Model (Section 5.2.8)

Name

Description

EQPS

equivalent plastic strain

TENSILE_EQPS

equivalent plastic strain only accumulated when the material is in tension (trace of stress tensor is positive)

RADIUS

radius of yield surface

BACK_STRESS

back stress (symmetric tensor)

YOUNGS_MODULUS

the current Young’s modulus as a function of temperature

POISSONS_RATIO

the current Poisson’s ratio as a function of temperature

YIELD_STRESS

the current yield stress as a function of temperature

ITERATIONS

radial return iterations

YIELD_FLAG

inside (0) or on (1) the yield surface
Table 5.8 State Variables for MULTILINEAR EP Model for Shells (Section 5.2.8)

Name

Description

EQPS

equivalent plastic strain

TENSILE_EQPS

equivalent plastic strain only accumulated when the material is in tension (trace of stress tensor is positive)

RADIUS

radius of yield surface

BACK_STRESS

back stress (symmetric tensor)

YOUNGS_MODULUS

the current Young’s modulus as a function of temperature

POISSONS_RATIO

the current Poisson’s ratio as a function of temperature

YIELD_STRESS

the current yield stress as a function of temperature

ITERATIONS

radial return iterations

ERROR

error in plane stress iterations

PS_ITER

plane stress iterations

5.2.9. Multilinear Elastic-Plastic Hardening Model with Failure

BEGIN PARAMETERS FOR MODEL ML_EP_FAIL
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Hardening behavior
  #
  YIELD STRESS       = <real>
  BETA               = <real> (1.0)
  HARDENING FUNCTION = <string> hardening_function_name
  #
  # Functions
  #
  YOUNGS MODULUS FUNCTION = <string> ym_function_name
  POISSONS RATIO FUNCTION = <string> pr_function_name
  YIELD STRESS FUNCTION   = <string> yield_stress_function_name
  #
  # Failure parameters
  #
  CRITICAL TEARING PARAMETER    = <real>
  CRITICAL CRACK OPENING STRAIN = <real>
  CRITICAL BIAXIALITY RATIO     = <real> critical_ratio(0.0)
  FAILURE EXPONENT              = <real> (4.0)
END [PARAMETERS FOR MODEL ML_EP_FAIL]

Like the ductile fracture model, the multilinear elastic-plastic fail model is an extension of an existing plasticity model (multilinear elastic-plastic) to include a ductile failure criteria. Again, the tearing parameter criterion and failure propagation model of Wellman [[7]] is selected. Specifically, this approach uses a failure criterion (the tearing parameter, \(t_p\)) that is based on the history of the plastic strain and stress states. Most failure criteria for ductile failure involve some form of the stress triaxiality, or the ratio of the pressure and the effective (shear) stress. The tearing parameter, however, is slightly different in that it depends on the pressure and the maximum principal stress and is given as,

(5.19)\[t_p = \int_{0}^{\varepsilon} \left\langle\frac{2\sigma_{\text{max}}}{3\left(\sigma_{\text{max}}-\sigma_{m}\right)} \right\rangle^m d\varepsilon_{p},\]

with \(\sigma_{\text{max}}\) and \(\sigma_{m}\) being the maximum principal and mean stresses, respectively. The exponent \(m\) is typically taken to be 4 while the \(\langle \cdot \rangle\) are Macaulay brackets defined as,

\[\begin{split}\langle x \rangle = \left\{\begin{array}{cc} 0 & x \leq 0 \\ x & x > 0\end{array} \right. ,\end{split}\]

and introduced so that failure only occurs and propagates under tensile stress states. Failure then initiates when the tearing parameter, \(t_p\), reaches a critical value, \(t_p^{\text{crit}}\). After this point, the stress decays (to 0) in a linear fashion according to the ratio of the crack opening strain in the maximum principal stress direction to its critical value, \(\varepsilon_{\text{ccos}}\). Modification and control of this latter parameter is important as it may be used to ensure consistent energy is dissipated through different meshes.

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input.

  • The beta parameter defines if hardening is isotropic or kinematic. See Section 5.1.6 for details on the beta parameter.

  • YIELD STRESS defines the stress for onset of yielding and plasticity.

  • The HARDENING FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope. The function describes the hardening behavior of the material as stress versus equivalent plastic strain. The x values of the function should be values of equivalent plastic strain while the y values of the function can be either the increment of stress over the yield stress or the actual stress at the corresponding equivalent plastic strain. Note the hardening function can have its first point defined at (0,0), or at (0, YIELD_STRESS). Either function definition behaves the same as only the slope of the hardening function between two strains is used by the model.

  • The YOUNGS MODULUS FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on Young’s modulus as a function of temperature.

  • The POISSONS RATIO FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on Poisson’s ratio as a function of temperature.

  • The YIELD STRESS FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on the yield stress as a function of temperature.

  • CRITICAL TEARING PARAMETER defines the \(t_{p}\) value at which fracture and subsequent decay of stress will occur.

  • When the model undergoes additionally strain after reaching the critical tearing parameter the stress in the model will decay to zero. The amount strain over which the stress decays to zero is defined with the CRITICAL CRACK OPENING STRAIN command line. The relevant opening strain is the component of strain that is aligned with the maximum-principal-stress direction at initial failure.

  • The CRITICAL BIAXIALITY RATIO command line should only be used under highly specific conditions and with extreme caution. It is intended only for the special case where the stress state is nearly biaxial, resulting in nearly identical principal strains. In this case, the eigenvector computation can give unreliable results for the direction vectors for the principal strains. If the ratio of the difference between two principal strains divided by their magnitude is less that the value specified by the CRITICAL BIAXIALITY RATIO command, the direction of the vector defining the crack opening strain will be given equal weight in each of the principal directions associated with those strains. The default value for the critical ratio is 0.0, which means that the principal directions will be accepted directly from the eigenvector computation. This command should only be used as a last resort if the loading is nearly biaxial and the default value has been demonstrated to lead to elements with high strains that are not failing long after reaching the critical tearing parameter.

  • The FAILURE EXPONENT command line specifies the exponent on the tearing parameter, the \(m\) parameter in (5.19). This exponent defaults to 4.0.

Output variables available for this model are listed in Table 5.9 and Table 5.10.

Table 5.9 State Variables for ML EP FAIL Model (Section 5.2.9)

Name

Variable Description

EQPS

Equivalent plastic strain

RADIUS

Radius of yield surface

BACK_STRESS

back stress - tensor

BACK_STRESS_XX

back stress - xx component

BACK_STRESS_YY

back stress - yy component

BACK_STRESS_ZZ

back stress - zz component

BACK_STRESS_XY

back stress - xy component

BACK_STRESS_YZ

back stress - yz component

BACK_STRESS_ZX

back stress - zx component

YOUNGS_MODULUS

Current Young’s modulus as a function of temperature

POISSONS_RATIO

Current Poisson’s ratio as a function of temperature

YIELD_STRESS

Current Yield stress as a function of temperature

TENSILE_EQPS

equivalent plastic strain only accumulated when the material is in tension (trace of stress tensor is positive

ITERATIONS

radial return iteration

YIELD_FLAG

inside(0) or on(1) yield surface

TEARING_PARAMETER

Current integrated value of the tearing parameter. Zero until yield is reached

CRACK_OPENING_STRAIN

Current value of the crack opening strain. Zero until the critical tearing parameter is reached

FAILURE_DIRECTION

crack opening direction at failure - vector

FAILURE_DIRECTION_X

crack opening direction at failure - x component

FAILURE_DIRECTION_Y

crack opening direction at failure - y component

FAILURE_DIRECTION_Z

crack opening direction at failure - z component

MAX_RADIUS

maximum radius at initial failure

MAX_PRESSURE

maximum stress pressure norm at initial failure

CRITICAL_CRACK_OPENING_STRAIN

CRITICAL_TEARING_PARAMETER
Table 5.10 State Variables for ML EP FAIL Model for Shells (Section 5.2.9)

Name

Variable Description

EQPS

equivalent plastic strain

RADIUS

radius of yield surface

BACK_STRESS

back stress - tensor

BACK_STRESS_XX

back stress - xx component

BACK_STRESS_YY

back stress - yy component

BACK_STRESS_ZZ

back stress - zz component

BACK_STRESS_XY

back stress - xy component

BACK_STRESS_YZ

back stress - yz component

BACK_STRESS_ZX

back stress - zx component

YOUNGS_MODULUS

Current Young’s modulus as a function of temperature

POISSONS_RATIO

Current Poisson’s ratio as a function of temperature

YIELD_STRESS

Current Yield stress as a function of temperature

ITER

radial return iterations

ERROR

Error in plane stress iterations

PS_ITER

Plane stress iterations

TEARING_PARAMETER

Current integrated value of the tearing parameter. Zero until yield is reached

CRACK_OPENING_STRAIN

Current value of the crack opening strain. Zero until the critical tearing parameter is reached

FAILURE_DIRECTION

crack opening direction at failure - vector

FAILURE_DIRECTION_X

crack opening direction at failure - x component

FAILURE_DIRECTION_Y

crack opening direction at failure - y component

FAILURE_DIRECTION_Z

crack opening direction at failure - z component

RADIUS_MAX

maximum radius at initial failure

TENSILE_EQPS

equivalent plastic strain only accumulated when the material is in tension (trace of stress tensor is positive)

5.2.10. Elastic-Plastic Hardening Model with Failure

BEGIN PARAMETERS FOR MODEL ELASTIC_PLASTIC_FAIL
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Isotropic/Kinematic hardening factor
  #
  BETA         = <real> (1.0)
  YIELD STRESS = <real>
  HARDENING FUNCTION      = <string>hardening_function_name
  POISSONS RATIO FUNCTION = <string>pr_function_name
  YIELD STRESS FUNCTION   = <string>yield_stress_function_name
  YOUNGS MODULUS FUNCTION = <string>ym_function_name
  #
  # Failure parameters
  #
  CRITICAL TEARING PARAMETER    = <real>crit_tearing
  CRITICAL CRACK OPENING STRAIN = <real>critical_strain
END [PARAMETERS FOR MODEL ELASTIC_PLASTIC_FAIL]

This model behaves identical to the ML_EP_FAIL (Section 5.2.9) material mode and only exists for legacy syntax compatibility purposes.

5.2.11. Thermoelastic-Plastic Model

BEGIN PARAMETERS FOR MODEL THERMOELASTIC_PLASTIC
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Isotropic/Kinematic hardening factor
  #
  BETA = <real>beta_parameter(1.0)
  YIELD STRESS = <real>yield_stress
  YOUNGS MODULUS FUNCTION = <string>ym_function_name
  POISSONS RATIO FUNCTION = <string>pr_function_name
  YIELD STRESS FUNCTION = <string>ys_function_name
  TEMPERATURES = <real(s)>temperature_values
  HARDENING FUNCTIONS = <string(s)>hardening_functions
END [PARAMETERS FOR MODEL THERMOELASTIC_PLASTIC]

The thermoelastic-plastic model is similar to the elastic-plastic model, but allows for temperature-dependent changes of the material properties. All elastic-plastic input parameters are still valid for the thermoelastic-plastic model, in addition to the temperature dependent functions.

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input.

  • The beta parameter defines if hardening is isotropic or kinematic. See Section 5.1.6 for details on the beta parameter.

  • The yield stress, the stress at which yield first initiates, is defined with the YIELD STRESS command line.

  • The YIELD STRESS FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on Yield Stress as a function of temperature.

  • The YOUNGS MODULUS FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on Young’s modulus as a function of temperature.

  • The POISSONS RATIO FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on Poisson’s ratio as a function of temperature.

  • The TEMPERATURES command line specifies the temperatures that correspond to the hardening functions defined in the HARDENING FUNCTIONS command line. The number of temperatures input here must match the number of hardening functions input.

  • The HARDENING FUNCTIONS command line references the names of the functions defined in a FUNCTION command line in the SIERRA scope that describes the hardening behavior for the material as stress versus equivalent plastic strain at the temperatures defined in the TEMPERATURES command line. The number of hardening functions input here must match the number of temperatures input. If the material temperature exactly matches one of the input temperatures the hardening of the material will exactly follow the hardening curve associated with that temperature. If the material temperature is bracketed by two hardening curves the actual hardening curve taken will be linearly interpolated between the bracketing curves. If the material temperature is either above the highest defined temperature function or below the lowest defined temperature function the closest hardening curve will be used for the material hardening.

Several plasticity models share the same underlying implementation. Output state variables available for this model are listed in Table Table 5.9. Note, depending on options used (temperature dependence of properties, failure, etc.) some of these state variables may not be computed.

5.2.12. Thermoelastic-Plastic Model with Failure

BEGIN PARAMETERS FOR MODEL THERMOELASTIC_PLASTIC_FAIL
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Isotropic/Kinematic hardening factor
  #
  BETA = <real>beta_parameter(1.0)
  TEMPERATURES = <real(s)>temperature_values
  YIELD STRESS = <real>yield_stress
  YOUNGS MODULUS FUNCTION = <string>ym_function_name
  POISSONS RATIO FUNCTION = <string>pr_function_name
  YIELD STRESS FUNCTION = <string>ys_function_name
  HARDENING FUNCTIONS = <string(s)>hardening_functions
  CRITICAL CRACK OPENING STRAIN = <real>critical_strain
  CRITICAL TEARING PARAMETER = <real>crit_tearing
  CRITICAL CRACK OPENING STRAIN FUNCTION
     = <string>crack_open_strain_function_name
  CRITICAL TEARING PARAMETER FUNCTION
     = <string>tearing_parameter_function_name
END [PARAMETERS FOR MODEL THERMOELASTIC_PLASTIC_FAIL]

The thermoelastic-plastic model with failure is similar to the ELASTIC_PLASTIC_FAIL material model, but allows for additional temperature-dependent changes of the material.

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input.

  • The beta parameter defines if hardening is isotropic or kinematic. See Section 5.1.6 for details on the beta parameter.

  • YIELD STRESS defines the stress for onset of yielding and plasticity.

  • The TEMPERATURES command line specifies the temperatures that correspond to the hardening functions defined in the HARDENING FUNCTIONS command line. The number of temperatures input here must match the number of hardening functions input.

  • The HARDENING FUNCTIONS command line references the names of the functions defined in a FUNCTION command line in the SIERRA scope that describes the hardening behavior for the material as stress versus equivalent plastic strain at the temperatures defined in the TEMPERATURES command line. The number of hardening functions input here must match the number of temperatures input. If the material temperature exactly matches one of the input temperatures the hardening of the material will exactly follow the hardening curve associated with that temperature. If the material temperature is bracketed by two hardening curves the actual hardening curve taken will be linearly interpolated between the bracketing curves. If the material temperature is either above the highest defined temperature function or below the lowest defined temperature function the closest hardening curve will be used for the material hardening.

  • The POISSONS RATIO FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on Poisson’s ratio as a function of temperature.

  • The YIELD STRESS FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on the yield stress as a function of temperature.

  • CRITICAL TEARING PARAMETER defines the \(t_{p}\) value at which fracture and subsequent decay of stress will occur.

  • When the model undergoes additionally strain after reaching the critical tearing parameter the stress in the model will decay to zero. The amount strain over which the stress decays to zero is defined with the CRITICAL CRACK OPENING STRAIN command line. The relevant opening strain is the component of strain that is aligned with the maximum-principal-stress direction at initial failure.

  • The CRITICAL CRACK OPENING STRAIN FUNCTION `` command line references the name of a function defined in a ``FUNCTION command line in the SIERRA scope that describes a scale factor on the crack opening strain as a function of temperature.

  • The CRITICAL TEARING PARAMETER FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes a scale factor on the tearing parameter as a function of temperature.

Several plasticity models share the same underlying implementation. Output state variables available for this model are listed in Table Table 5.9. Note, depending on options used (temperature dependence of properties, failure, etc.) some of these state variables may not be computed.

5.2.13. J2 Plasticity Model

BEGIN PARAMETERS FOR MODEL J2_PLASTICITY
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Yield surface parameters
  #
  YIELD STRESS = <real>
  BETA         = <real> (1.0)
  #
  # Hardening model
  #
  HARDENING MODEL = LINEAR | POWER_LAW | VOCE | USER_DEFINED |
  FLOW_STRESS | DECOUPLED_FLOW_STRESS | JOHNSON_COOK |
  POWER_LAW_BREAKDOWN
  #
  # Linear hardening
  #
  HARDENING MODULUS = <real>
  #
  # Power-law hardening
  #
  HARDENING CONSTANT = <real>
  HARDENING EXPONENT = <real> (0.5)
  LUDERS STRAIN      = <real> (0.0)
  #
  # Voce hardening
  #
  HARDENING MODULUS       = <real>
  EXPONENTIAL COEFFICIENT = <real>
  #
  # Johnson-Cook hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  RATE CONSTANT      = <real>
  REFERENCE RATE     = <real>
  #
  # Power law breakdown hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  RATE COEFFICIENT   = <real>
  RATE EXPONENT      = <real>
  # User defined hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  #
  #
  # Following Commands Pertain to Flow_Stress Hardening Model
  #
  #    -  Isotropic Hardening model
  #
  ISOTROPIC HARDENING MODEL = LINEAR | POWER_LAW | VOCE |
                              USER_DEFINED
  #
  # Specifications for Linear, Power-law, and Voce same as above
  #
  # User defined hardening
  #
  ISOTROPIC HARDENING FUNCTION = <string>iso_hardening_fun_name
  #
  #     - Rate dependence
  #
  RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
     USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  # Specifications for Johnson-Cook, Power-law-breakdown
  #     same as before EXCEPT no need to specify a
  #     hardening function
  #
  # User defined rate multiplier
  #
  RATE MULTIPLIER FUNCTION = <string> rate_mult_function_name
  #
  #     - Temperature dependence
  #
  TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
     TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #  Johnson-Cook temperature dependence
  #
  MELTING TEMPERATURE   = <real>
  REFERENCE TEMPERATURE = <real>
  TEMPERATURE EXPONENT  = <real>
  #
  #  User-defined temperature dependence
  TEMPERATURE MULTIPLIER FUNCTION = <string>temp_mult_function_name
  #
  # Following Commands Pertain to Decoupled_Flow_Stress Hardening Model
  #
  #    -  Isotropic Hardening model
  #
  ISOTROPIC HARDENING MODEL = LINEAR | POWER_LAW | VOCE | USER_DEFINED
  #
  # Specifications for Linear, Power-law, and Voce same as above
  #
  # User defined hardening
  #
  ISOTROPIC HARDENING FUNCTION = <string>isotropic_hardening_function_name
  #
  #     - Rate dependence
  #
  YIELD RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
              USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  # Specifications for Johnson-Cook, Power-law-breakdown same as before
  #     EXCEPT no need to specify a hardening function
  #     AND should be preceded by YIELD
  #
  #     As an example for Johnson-Cook yield rate dependence,
  #
  YIELD RATE CONSTANT  = <real>
  YIELD REFERENCE RATE = <real>
  #
  # User defined rate multiplier
  #
  YIELD RATE MULTIPLIER FUNCTION = <string>yield_rate_mult_function_name
  #
  HARDENING_RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
              USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  #     Syntax same as for yield parameters but with a HARDENING prefix
  #
  #     - Temperature dependence
  #
  YIELD TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
            TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #  Johnson-Cook temperature dependence
  #
  YIELD MELTING TEMPERATURE   = <real>
  YIELD REFERENCE TEMPERATURE = <real>
  YIELD TEMPERATURE EXPONENT  = <real>
  #
  #  User-defined temperature dependence
  YIELD TEMPERATURE MULTIPLIER FUNCTION = <string>yield_temp_mult_fun_name
  #
  HARDENING TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
            TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #   Syntax for hardening constants same as for yield but
  #            with HARDENING prefix
  #
  # Optional Failure Definitions
  #    Following only need to be defined if intend to use failure model
  #
  FAILURE MODEL = TEARING_PARAMETER | JOHNSON_COOK_FAILURE | WILKINS
                  | MODULAR_FAILURE | MODULAR_BCJ_FAILURE

  CRITICAL FAILURE PARAMETER = <real>
  #
  # TEARING_PARAMETER Failure model definitions
  #
  TEARING PARAMETER EXPONENT = <real>
  #
  # JOHNSON_COOK_FAILURE Failure model definitions
  #
  JOHNSON COOK D1       = <real>
  JOHNSON COOK D2       = <real>
  JOHNSON COOK D3       = <real>
  JOHNSON COOK D4       = <real>
  JOHNSON COOK D5       = <real>
  #
  #Following Johnson-Cook parameters can only be defined once.  As such, only
  #  needed if not previously defined via Johnson-Cook multipliers
  #  w/ flow-stress hardening.  Does need to be defined
  #  w/ Decoupled Flow Stress
  #
  REFERENCE RATE        = <real>
  REFERENCE TEMPERATURE = <real>
  MELTING TEMPERATURE   = <real>
  #
  # WILKINS Failure model definitions
  #
  WILKINS ALPHA    = <real>
  WILKINS BETA     = <real>
  WILKINS PRESSURE = <real>
  #
  #  MODULAR_FAILURE Failure model definitions
  #
  PRESSURE MULTIPLIER         = PRESSURE_INDEPENDENT | WILKINS
                                | USER_DEFINED (PRESSURE_INDEPENDENT)
  LODE ANGLE MULTIPLIER       = LODE_ANGLE_INDEPENDENT |
                                WILKINS (LODE_ANGLE_INDEPENDENT)
  TRIAXIALITY MULTIPLIER      = TRIAXIALITY_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (TRIAXIALITY_INDEPENDENT)
  RATE FAIL MULTIPLIER        = RATE_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (RATE_INDEPENDENT)
  TEMPERATURE FAIL MULTIPLIER = TEMPERATURE_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (TEMPERATURE_INDEPENDENT)
  #
  # Individual multiplier definitions
  #
  PRESSURE MULTIPLIER = WILKINS
  WILKINS ALPHA       = <real>
  WILKINS PRESSURE    = <real>
  #
  PRESSURE MULTIPLIER = USER_DEFINED
  PRESSURE MULTIPLIER FUNCTION = <string> pressure_multiplier_fun_name
  #
  LODE ANGLE MULTIPLIER = WILKINS
  WILKINS BETA          = <real>
  #
  TRIAXIALITY MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D1        = <real>
  JOHNSON COOK D2        = <real>
  JOHNSON COOK D3        = <real>
  #
  TRIAXIALITY MULTIPLIER = USER_DEFINED
  TRIAXIALITY MULTIPLIER FUNCTION = <string> triaxiality_multiplier_fun_name
  #
  RATE FAIL MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D4      = <real>
  # REFERENCE RATE should only be added if not previously defined
  REFERENCE RATE       = <real>
  #
  RATE FAIL MULTIPLIER = USER_DEFINED
  RATE FAIL MULTIPLIER FUNCTION = <string> rate_fail_multiplier_fun_name
  #
  TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D5             = <real>
  # JC Temperatures should only be defined if not previously given
  REFERENCE TEMPERATURE       = <real>
  MELTING TEMPERATURE         = <real>
  #
  TEMPERATURE FAIL MULTIPLIER          = USER_DEFINED
  TEMPERATURE FAIL MULTIPLIER FUNCTION = <string> temp_multiplier_fun_name
  #
  # MODULAR_BCJ_FAILURE Failure model definitions
  #
  INITIAL DAMAGE    = <real>
  INITIAL VOID SIZE = <real>
  DAMAGE BETA       = <real> (0.5)
  GROWTH MODEL      = COCKS_ASHBY | NO_GROWTH (NO_GROWTH)
  NUCLEATION MODEL  = HORSTEMEYER_GOKHALE | CHU_NEEDLEMAN_STRAIN
                      | NO_NUCLEATION (NO_NUCLEATION)
  #
  GROWTH RATE FAIL MULTIPLIER        = JOHNSON_COOK | USER_DEFINED
                                       | RATE_INDEPENDENT
                                       (RATE_INDEPENDENT)
  GROWTH TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK | USER_DEFINED
                                       | TEMPERATURE_INDEPENDENT
                                       (TEMPERATURE_INDEPENDENT)
  #
  NUCLEATION RATE FAIL MULTIPLIER        = JOHNSON_COOK | USER_DEFINED
                                           | RATE_INDEPENDENT
                                           (RATE_INDEPENDENT)
  NUCLEATION TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK | USER_DEFINED
                                           | TEMPERATURE_INDEPENDENT
                                           (TEMPERATURE_INDEPENDENT)
  #
  # Definitions for individual growth and nucleation models
  #
  GROWTH MODEL = COCKS_ASHBY
  DAMAGE EXPONENT = <real> (0.5)
  #
  NUCLEATION MODEL      = HORSTEMEYER_GOKHALE
  NUCLEATION PARAMETER1 = <real> (0.0)
  NUCLEATION PARAMETER2 = <real> (0.0)
  NUCLEATION PARAMETER3 = <real> (0.0)
  #
  NUCLEATION MODEL          = CHU_NEEDLEMAN_STRAIN
  NUCLEATION AMPLITUDE      = <real>
  MEAN NUCLEATION STRAIN    = <real>
  NUCLEATION STRAIN STD DEV = <real>
  #
  # Definitions for rate and temperature fail multiplier
  #   Note: only showing definitions for growth.
  #    Nucleation terms are the same just with NUCLEATION instead
  #    of GROWTH
  #
  GROWTH RATE FAIL MULTIPLIER = JOHNSON_COOK
  GROWTH JOHNSON COOK D4      = <real>
  GROWTH REFERENCE RATE       = <real>
  #
  GROWTH RATE FAIL MULTIPLIER          = USER_DEFINED
  GROWTH RATE FAIL MULTIPLIER FUNCTION = <string> growth_rate_fail_mult_func
  #
  GROWTH TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK
  GROWTH JOHNSON COOK D5             = <real>
  GROWTH REFERENCE TEMPERATURE       = <real>
  GROWTH MELTING TEMPERATURE         = <real>
  #
  GROWTH TEMPERATURE FAIL MULTIPLIER          = USER_DEFINED
  GROWTH TEMPERATURE FAIL MULTIPLIER FUNCTION = <string> temp_fail_mult_func
  #
  #
  # Optional Adiabatic Heating/Thermal Softening  Definitions
  #    Following only need to be defined if intend to use failure model
  #
  THERMAL SOFTENING MODEL = ADIABATIC | COUPLED
  #
  SPECIFIC HEAT = <real> # not needed for COUPLED
  BETA_TQ       = <real>
END [PARAMETERS FOR MODEL J2_PLASTICITY]

The \(J_2\) plasticity model is a generic implementation of a von Mises yield surface with kinematic and isotropic hardening features. Unlike other models (e.g. Elastic-Plastic, Elastic-Plastic Power Law) more flexible, general hardening forms are implemented enabling different isotropic hardening descriptions and some rate and/or temperature dependence.

As is common to other plasticity models in LAMÉ, the \(J_2\) plasticity model uses a hypoelastic formulation. As such, the total rate of deformation is additively decomposed into an elastic and plastic part such that

\[D_{ij}=D^{\text{e}}_{ij}+D^{\text{p}}_{ij}.\]

The objective stress rate, depending only on the elastic deformation, may then be written as,

\[\stackrel{\circ}{\sigma}_{ij}=\mathbb{C}_{ijkl}D^{\text{e}}_{kl},\]

where \(\mathbb{C}_{ijkl}\) is the fourth-order elastic, isotropic stiffness tensor.

The yield surface for the \(J_2\) plasticity model, \(f\), may be written,

(5.20)\[f\left(\sigma_{ij},\alpha_{ij},\bar{\varepsilon}^p,\dot{\bar{\varepsilon}}^p,\theta\right)=\phi\left(\sigma_{ij},\alpha_{ij}\right)-\bar{\sigma}\left(\bar{\varepsilon}^p,\dot{\bar{\varepsilon}}^p,\theta\right),\]

in which \(\alpha_{ij},\bar{\varepsilon}^p,\dot{\bar{\varepsilon}}^p,\) and \(\theta\) are the kinematic backstress, equivalent plastic strain, equivalent plastic strain rate, and absolute temperature, respectively, while \(\phi\) and \(\bar{\sigma}\) are the effective stress and a generic form of the flow stress. Broadly speaking, the effective stress describes the shape of the yield surface and kinematic effects while the flow stress gives the size of the current yield surface. It should also be noted that in writing the yield surface in this way, the dependence on the state variables is split between the effective stress and flow stress functions.

For \(J_2\) plasticity, the effective stress is given as,

\[\phi^2\left(\sigma_{ij},\alpha_{ij}\right)=\frac{3}{2}\left(s_{ij}-\alpha_{ij}\right)\left(s_{ij}-\alpha_{ij}\right),\]

with \(s_{ij}\) being the deviatoric stress defined as \(s_{ij}=\sigma_{ij}-(1/3)\sigma_{kk}\delta_{ij}\). For the flow stress, a general representation of the form,

\[\bar{\sigma}\left(\bar{\varepsilon}^p,\dot{\bar{\varepsilon}}^p,\theta\right)=\sigma_y\hat{\sigma}_{\text{y}}\left(\dot{\bar{\varepsilon}}^p\right)\breve{\sigma}_{\text{y}}\left(\theta\right)+K\left(\bar{\varepsilon}^p\right)\hat{\sigma}_{\text{h}}\left(\dot{\bar{\varepsilon}}^p\right)\breve{\sigma}_{\text{h}}\left(\theta\right),\]

is allowed. In this fashion, the effects of rate (\(\hat{\sigma}_{\text{y,h}}\)) and temperature (\(\breve{\sigma}_{\text{y,h}}\)) dependence on yield (\(\sigma_y\)) and isotropic hardening (\(K\left(\bar{\varepsilon}^p\right)\)) are decomposed. Separate temperature and rate dependencies may be be specified for yield (subscript y) and hardening (h). This assumption is an extension of the multiplicative decomposition of the Johnson-Cook model [[8], [9]]. It should be noted that not all effects need to be included and the default parameterization of the hardening classes is such that the response is rate and temperature independent. The following section on plastic hardening will go into more detail on possible choices for functional representations.

An associated flow rule is utilized such that the plastic rate of deformation is normal to the yield surface and is given by,

\[D_{ij}^{\text{p}}=\dot{\gamma}\frac{\partial\phi}{\partial\sigma_{ij}}=\dot{\gamma}\frac{3}{2\phi}s_{ij},\]

where \(\dot{\gamma}\) is the consistency multiplier enforcing \(f=0\) during plastic deformation. Given the form of \(f\), it can also be shown that \(\dot{\gamma}=\dot{\bar{\varepsilon}}^p\).

Additional discussion on options for failure models and adiabatic heating may be found in [[10], [11]] and [[12]], respectively.

In the command blocks that define the \(J_2\) plasticity model:

  • The reference nominal yield stress, \(\bar{\sigma}\), is defined with the YIELD STRESS command line.

  • The beta parameter defines if hardening is isotropic.

  • The type of hardening law is defined with the HARDENING MODEL command line, other hardening commands then define the specific shape of that hardening curve.

  • The hardening modulus for a linear hardening model is defined with the HARDENING MODULUS command line.

  • The hardening constant for a power law hardening model is defined with the HARDENING CONSTANT command line.

  • The hardening exponent for a power law hardening model is defined with the HARDENING EXPONENT command line.

  • The Luders strain for a power law hardening model is defined with the LUDERS STRAIN command line.

  • The hardening function for a user defined hardening model is defined with the HARDENING FUNCTION command line.

  • The shape of the spline for the spline based hardening is defined by the CUBIC SPLINE TYPE, CARDINAL PARAMETER, KNOT EQPS, and KNOT STRESS command lines.

  • The isotropic hardening model for the flow stress hardening model is defined with the ISOTROPIC HARDENING MODEL command line.

  • The function name of a user-defined isotropic hardening model is defined via the ISOTROPIC HARDENING FUNCTION command line.

  • The optional rate multiplier for the flow stress hardening model is defined with the RATE MULTIPLIER command line.

  • The optional temperature multiplier for the flow stress hardening model is defined via the TEMPERATURE MULTIPLIER command line.

  • The function name of a user-defined temperature multiplier is defined with the TEMPERATURE MULTIPLIER FUNCTION command line.

  • For a Johnson-Cook temperature multiplier, the melting temperature, \(\theta_{\text{melt}}\), is defined via the MELTING TEMPERATURE command line.

  • For a Johnson-Cook temperature multiplier, the reference temperature, \(\theta_{\text{ref}}\), is defined via the REFERENCE TEMPERATURE command line.

  • For a Johnson-Cook temperature multiplier, the temperature exponent, \(M\), is defined via the TEMPERATURE EXPONENT command line.

  • The optional rate multiplier for the yield stress for the decoupled flow stress hardening model is defined with the YIELD RATE MULTIPLIER command line.

  • The optional rate multiplier for the hardening for the decoupled flow stress hardening model is defined with the HARDENING RATE MULTIPLIER command line.

  • The optional temperature multiplier for the yield stress for the decoupled flow stress hardening model is defined with the YIELD TEMPERATURE MULTIPLIER command line.

  • The optional temperature multiplier for the hardening for the decoupled flow stress hardening model is defined via the HARDENING TEMPERATURE MULTIPLIER command line.

Output variables available for this model are listed in Table 5.11.

Table 5.11 State Variables for J2 PLASTICITY Model

Name

Description

EQPS

equivalent plastic strain, \(\bar{\varepsilon}^{p}\)

EQDOT

equivalent plastic strain rate, \(\dot{\bar{\varepsilon}}^{p}\)

SEFF

effective stress, \(\phi\)

TENSILE_EQPS

tensile equivalent plastic strain, \(\bar{\varepsilon}^{p}_{t}\)

DAMAGE

damage, \(\phi\)

VOID_COUNT

void count, \(\eta\)

VOID_SIZE

void size, \(\upsilon\)

DAMAGE_DOT

damage rate, \(\dot{\phi}\)

VOID_COUNT_DOT

void count rate, \(\dot{\eta}\)

PLASTIC_WORK_HEAT_RATE

plastic work heat rate, \(\dot{Q}^p\)

5.2.14. Hosford Plasticity Model

BEGIN PARAMETERS FOR MODEL HOSFORD_PLASTICITY
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Yield surface parameters
  #
  YIELD STRESS = <real>
  A            = <real> (1.0)
  #
  # Hardening model
  #
  HARDENING MODEL = LINEAR | POWER_LAW | VOCE | USER_DEFINED |
    FLOW_STRESS | DECOUPLED_FLOW_STRESS | JOHNSON_COOK |
    POWER_LAW_BREAKDOWN
  #
  # Linear hardening
  #
  HARDENING MODULUS = <real>
  #
  # Power-law hardening
  #
  HARDENING CONSTANT = <real>
  HARDENING EXPONENT = <real> (0.5)
  LUDERS STRAIN      = <real> (0.0)
  #
  # Voce hardening
  #
  HARDENING MODULUS       = <real>
  EXPONENTIAL COEFFICIENT = <real>
  #
  # Johnson-Cook hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  RATE CONSTANT      = <real>
  REFERENCE RATE     = <real>
  #
  # Power law breakdown hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  RATE COEFFICIENT   = <real>
  RATE EXPONENT      = <real>
  # User defined hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  #
  #
  # Following Commands Pertain to Flow_Stress Hardening Model
  #
  #    -  Isotropic Hardening model
  #
  ISOTROPIC HARDENING MODEL = LINEAR | POWER_LAW | VOCE |
                              USER_DEFINED
  #
  # Specifications for Linear, Power-law, and Voce same as above
  #
  # User defined hardening
  #
  ISOTROPIC HARDENING FUNCTION = <string>iso_hardening_fun_name
  #
  #     - Rate dependence
  #
  RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
     USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  # Specifications for Johnson-Cook, Power-law-breakdown
  #     same as before EXCEPT no need to specify a
  #     hardening function
  #
  # User defined rate multiplier
  #
  RATE MULTIPLIER FUNCTION = <string> rate_mult_function_name
  #
  #     - Temperature dependence
  #
  TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
     TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #  Johnson-Cook temperature dependence
  #
  MELTING TEMPERATURE   = <real>
  REFERENCE TEMPERATURE = <real>
  TEMPERATURE EXPONENT  = <real>
  #
  #  User-defined temperature dependence
  TEMPERATURE MULTIPLIER FUNCTION = <string>temp_mult_function_name
  #
  # Following Commands Pertain to Decoupled_Flow_Stress Hardening Model
  #
  #    -  Isotropic Hardening model
  #
  ISOTROPIC HARDENING MODEL = LINEAR | POWER_LAW | VOCE | USER_DEFINED
  #
  # Specifications for Linear, Power-law, and Voce same as above
  #
  # User defined hardening
  #
  ISOTROPIC HARDENING FUNCTION = <string>isotropic_hardening_function_name
  #
  #     - Rate dependence
  #
  YIELD RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
              USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  # Specifications for Johnson-Cook, Power-law-breakdown same as before
  #     EXCEPT no need to specify a hardening function
  #     AND should be preceded by YIELD
  #
  #     As an example for Johnson-Cook yield rate dependence,
  #
  YIELD RATE CONSTANT  = <real>
  YIELD REFERENCE RATE = <real>
  #
  # User defined rate multiplier
  #
  YIELD RATE MULTIPLIER FUNCTION = <string>yield_rate_mult_function_name
  #
  HARDENING_RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
              USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  #     Syntax same as for yield parameters but with a HARDENING prefix
  #
  #     - Temperature dependence
  #
  YIELD TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
            TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #  Johnson-Cook temperature dependence
  #
  YIELD MELTING TEMPERATURE   = <real>
  YIELD REFERENCE TEMPERATURE = <real>
  YIELD TEMPERATURE EXPONENT  = <real>
  #
  #  User-defined temperature dependence
  YIELD TEMPERATURE MULTIPLIER FUNCTION = <string>yield_temp_mult_fun_name
  #
  HARDENING TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
            TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #   Syntax for hardening constants same as for yield but
  #            with HARDENING prefix
  #
  # Optional Failure Definitions
  #    Following only need to be defined if intend to use failure model
  #
  FAILURE MODEL = TEARING_PARAMETER | JOHNSON_COOK_FAILURE | WILKINS
                  | MODULAR_FAILURE | MODULAR_BCJ_FAILURE

  CRITICAL FAILURE PARAMETER = <real>
  #
  # TEARING_PARAMETER Failure model definitions
  #
  TEARING PARAMETER EXPONENT = <real>
  #
  # JOHNSON_COOK_FAILURE Failure model definitions
  #
  JOHNSON COOK D1       = <real>
  JOHNSON COOK D2       = <real>
  JOHNSON COOK D3       = <real>
  JOHNSON COOK D4       = <real>
  JOHNSON COOK D5       = <real>
  #
  #Following Johnson-Cook parameters can only be defined once.  As such, only
  #  needed if not previously defined via Johnson-Cook multipliers
  #  w/ flow-stress hardening.  Does need to be defined
  #  w/ Decoupled Flow Stress
  #
  REFERENCE RATE        = <real>
  REFERENCE TEMPERATURE = <real>
  MELTING TEMPERATURE   = <real>
  #
  # WILKINS Failure model definitions
  #
  WILKINS ALPHA    = <real>
  WILKINS BETA     = <real>
  WILKINS PRESSURE = <real>
  #
  #  MODULAR_FAILURE Failure model definitions
  #
  PRESSURE MULTIPLIER         = PRESSURE_INDEPENDENT | WILKINS
                                | USER_DEFINED (PRESSURE_INDEPENDENT)
  LODE ANGLE MULTIPLIER       = LODE_ANGLE_INDEPENDENT |
                                WILKINS (LODE_ANGLE_INDEPENDENT)
  TRIAXIALITY MULTIPLIER      = TRIAXIALITY_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (TRIAXIALITY_INDEPENDENT)
  RATE FAIL MULTIPLIER        = RATE_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (RATE_INDEPENDENT)
  TEMPERATURE FAIL MULTIPLIER = TEMPERATURE_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (TEMPERATURE_INDEPENDENT)
  #
  # Individual multiplier definitions
  #
  PRESSURE MULTIPLIER = WILKINS
  WILKINS ALPHA       = <real>
  WILKINS PRESSURE    = <real>
  #
  PRESSURE MULTIPLIER = USER_DEFINED
  PRESSURE MULTIPLIER FUNCTION = <string> pressure_multiplier_fun_name
  #
  LODE ANGLE MULTIPLIER = WILKINS
  WILKINS BETA          = <real>
  #
  TRIAXIALITY MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D1        = <real>
  JOHNSON COOK D2        = <real>
  JOHNSON COOK D3        = <real>
  #
  TRIAXIALITY MULTIPLIER = USER_DEFINED
  TRIAXIALITY MULTIPLIER FUNCTION = <string> triaxiality_multiplier_fun_name
  #
  RATE FAIL MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D4      = <real>
  # REFERENCE RATE should only be added if not previously defined
  REFERENCE RATE       = <real>
  #
  RATE FAIL MULTIPLIER = USER_DEFINED
  RATE FAIL MULTIPLIER FUNCTION = <string> rate_fail_multiplier_fun_name
  #
  TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D5             = <real>
  # JC Temperatures should only be defined if not previously given
  REFERENCE TEMPERATURE       = <real>
  MELTING TEMPERATURE         = <real>
  #
  TEMPERATURE FAIL MULTIPLIER          = USER_DEFINED
  TEMPERATURE FAIL MULTIPLIER FUNCTION = <string> temp_multiplier_fun_name
  #
  # MODULAR BCJ_FAILURE Failure model definitions
  #
  INITIAL DAMAGE    = <real>
  INITIAL VOID SIZE = <real>
  DAMAGE BETA       = <real> (0.5)
  GROWTH MODEL      = COCKS_ASHBY | NO_GROWTH (NO_GROWTH)
  NUCLEATION MODEL  = HORSTEMEYER_GOKHALE | CHU_NEEDLEMAN_STRAIN
                      | NO_NUCLEATION (NO_NUCLEATION)
  #
  GROWTH RATE FAIL MULTIPLIER        = JOHNSON_COOK | USER_DEFINED
                                       | RATE_INDEPENDENT
                                       (RATE_INDEPENDENT)
  GROWTH TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK | USER_DEFINED
                                       | TEMPERATURE_INDEPENDENT
                                       (TEMPERATURE_INDEPENDENT)
  #
  NUCLEATION RATE FAIL MULTIPLIER        = JOHNSON_COOK | USER_DEFINED
                                           | RATE_INDEPENDENT
                                           (RATE_INDEPENDENT)
  NUCLEATION TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK | USER_DEFINED
                                           | TEMPERATURE_INDEPENDENT
                                           (TEMPERATURE_INDEPENDENT)
  #
  # Definitions for individual growth and nucleation models
  #
  GROWTH MODEL = COCKS_ASHBY
  DAMAGE EXPONENT = <real> (0.5)
  #
  NUCLEATION MODEL      = HORSTEMEYER_GOKHALE
  NUCLEATION PARAMETER1 = <real> (0.0)
  NUCLEATION PARAMETER2 = <real> (0.0)
  NUCLEATION PARAMETER3 = <real> (0.0)
  #
  NUCLEATION MODEL          = CHU_NEEDLEMAN_STRAIN
  NUCLEATION AMPLITUDE      = <real>
  MEAN NUCLEATION STRAIN    = <real>
  NUCLEATION STRAIN STD DEV = <real>
  #
  # Definitions for rate and temperature fail multiplier
  #   Note: only showing definitions for growth.
  #    Nucleation terms are the same just with NUCLEATION instead
  #    of GROWTH
  #
  GROWTH RATE FAIL MULTIPLIER = JOHNSON_COOK
  GROWTH JOHNSON COOK D4      = <real>
  GROWTH REFERENCE RATE       = <real>
  #
  GROWTH RATE FAIL MULTIPLIER          = USER_DEFINED
  GROWTH RATE FAIL MULTIPLIER FUNCTION = <string> growth_rate_fail_mult_func
  #
  GROWTH TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK
  GROWTH JOHNSON COOK D5             = <real>
  GROWTH REFERENCE TEMPERATURE       = <real>
  GROWTH MELTING TEMPERATURE         = <real>
  #
  GROWTH TEMPERATURE FAIL MULTIPLIER          = USER_DEFINED
  GROWTH TEMPERATURE FAIL MULTIPLIER FUNCTION = <string> temp_fail_mult_func
  #
  #
  # Optional Adiabatic Heating/Thermal Softening  Definitions
  #    Following only need to be defined if intend to use failure model
  #
  THERMAL SOFTENING MODEL = ADIABATIC | COUPLED
  #
  SPECIFIC HEAT = <real> #not needed for COUPLED
  BETA_TQ       = <real>
END [PARAMETERS FOR MODEL HOSFORD_PLASTICITY]

Like other elastic-plastic models in LAMÉ, the Hosford plasticity model is a rate-independent hypoelastic formulation. Unlike the Hill and other more complex plasticity models, it is isotropic. In a similar fashion to those models, the total rate of deformation is additively decomposed into an elastic and plastic part such that

\[D_{ij}=D^{\text{e}}_{ij}+D^{\text{p}}_{ij}.\]

The objective stress rate, depending only on the elastic deformation, may then be written as,

\[\stackrel{\circ}{\sigma}_{ij}=\mathbb{C}_{ijkl}D^{\text{e}}_{kl}.\]

The Hosford plasticity model utilizes a yield surface first put forth by W. F. Hosford in the 1970’s [[13]] that is isotropic but non-quadratic. This specific form was proposed due to experimental observations of biaxial stretching in which neither the Tresca or \(J_2\) yield surfaces could describe the results. In contrast to many of the yield surfaces proposed for similar purposes, only two parameters are utilized. Even with these limited terms, the developed model is quite versatile and can be reduced to von Mises or Tresca conditions as well as capturing responses in between. This yield surface is given as,

\[f\left(\sigma_{ij},\bar{\varepsilon}^p\right)=\phi\left(\sigma_{ij}\right)-\bar{\sigma}\left(\bar{\varepsilon}^p\right)=0,\]

in which \(\phi\left(\sigma_{ij}\right)\) is the Hosford effective stress and \(\bar{\sigma}\left(\bar{\varepsilon}^p\right)\) is the current yield stress that may depend on rate and/or temperature. The Hosford effective stress is a non-quadratic function of the principal stresses (\(\sigma_i, i=1,2,3\)) and is given as

\[\phi\left(\sigma_{ij}\right)=\left[\frac{|\sigma_1-\sigma_2|^a+|\sigma_2-\sigma_3|^a+|\sigma_1-\sigma_3|^a}{2}\right]^{1/a}\]

in which \(a\) is the yield surface exponent. Interestingly, if \(a=2\) or \(4\) the yield surface reduces to that of a \(J_2\) von Mises surface while \(a=1\) or as \(a\rightarrow\infty\) produces a Tresca like shape. If the value of \(a\) is above 4 the yield surface takes a position between the Tresca and \(J_2\) limits. Typical values are \(a=6\) or \(a=8\) for bcc and fcc metals, respectively [[14]]. To highlight this variability the yield surface is plotted below in Fig. 5.7 for three values of \(a\) – \(a = 4, 8,\) and 100.

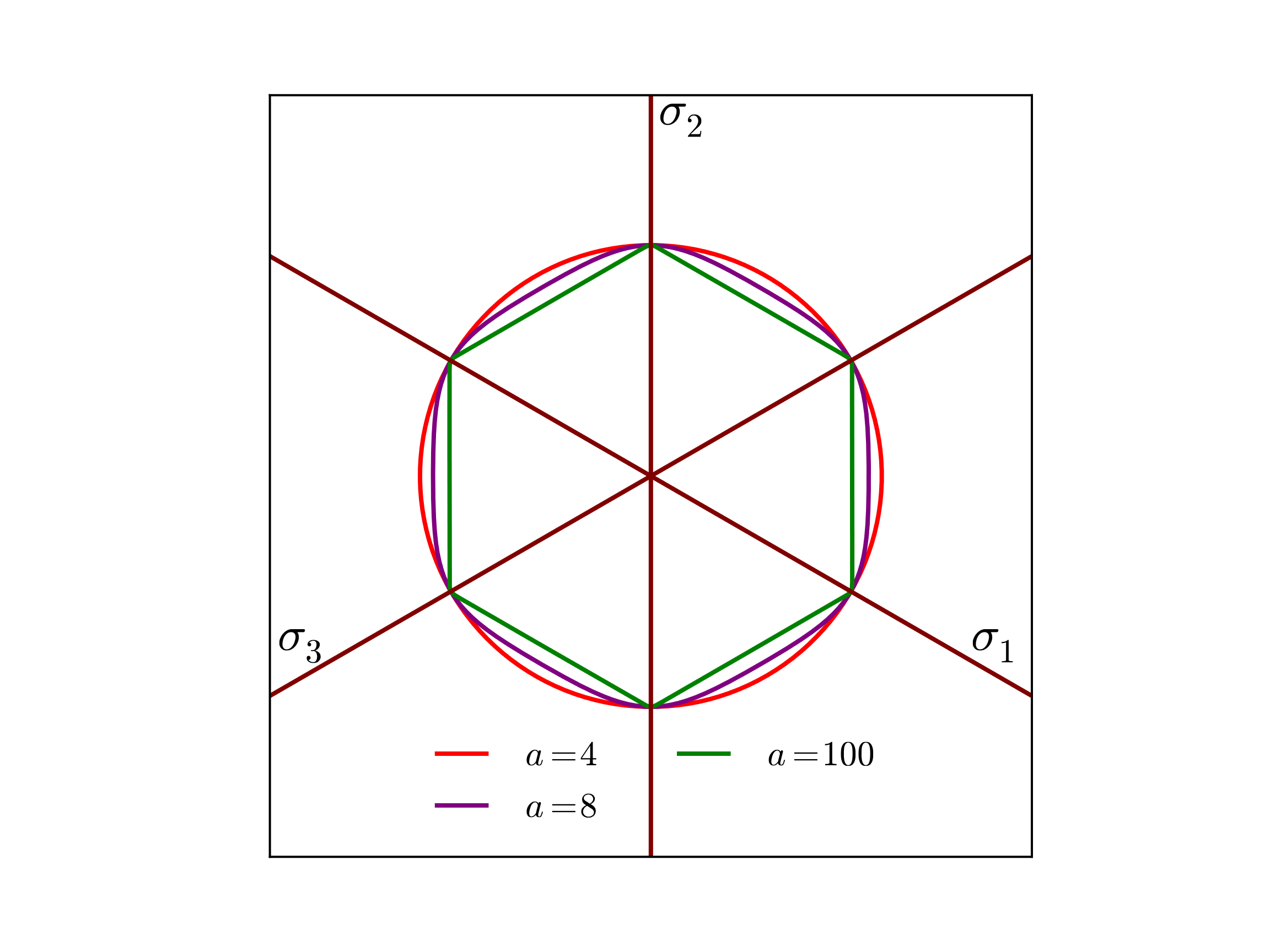
../../_images/hosfordSurface.png

Fig. 5.7 Example Hosford yield surfaces, \(f\left(\sigma_{ij},\bar{\varepsilon}^p=0;a\right)\), presented in the deviatoric \(\pi\)-plane. The presented surfaces correspond to the different yield exponents \(a = 4, 8,\) and \(100\).

For the hardening function, \(\bar{\sigma}\left(\bar{\varepsilon}^p\right)\), a variety of forms including linear, power law, or a more general user defined function may be used.

An associated flow rule is utilized such that the plastic rate of deformation is normal to the yield surface and is given by,

\[\dot{D}_{ij}^{\text{p}}=\dot{\gamma}\frac{\partial\phi}{\partial\sigma_{ij}},\]

where \(\dot{\gamma}\) is the consistency multiplier enforcing \(f=0\) during plastic deformation. Given the form of \(f\), it can also be shown that \(\dot{\gamma}=\dot{\bar{\varepsilon}}^p\).

For details on the plasticity model, please see [[15]]. Additional details on failure models and adiabatic heating capabilities may be found in [[10], [11]] and [[12]], respectively.

In the command blocks that define the Hosford plasticity model:

  • See Section 5.1.5 for more information on elastic constants input.

  • The reference nominal yield stress, \(\bar{\sigma}\), is defined with the YIELD STRESS command line.

  • The yield surface exponent, \(a\), is defined with the A command line.

  • The type of hardening law is defined with the HARDENING MODEL command line, other hardening commands then define the specific shape of that hardening curve.

  • The hardening modulus for a linear hardening model is defined with the HARDENING MODULUS command line.

  • The hardening constant for a power law hardening model is defined with the HARDENING CONSTANT command line.

  • The hardening exponent for a power law hardening model is defined with the HARDENING EXPONENT command line.

  • The L"{u}ders strain for a power law hardening model is defined with the LUDERS STRAIN command line.

  • The hardening function for a user defined hardening model is defined with the HARDENING FUNCTION command line.

  • The shape of the spline for the spline based hardening is defined by the CUBIC SPLINE TYPE, CARDINAL PARAMETER, KNOT EQPS, and KNOT STRESS command lines.

Output variables available for this model are listed in Table 5.12.

Table 5.12 State Variables for HOSFORD PLASTICITY Model (Section 5.2.14)

Name

Description

EQPS

equivalent plastic strain, \(\bar{\varepsilon}^{p}\)

EQDOT

equivalent plastic strain rate, \(\dot{\bar{\varepsilon}}^{p}\)

SEFF

effective stress, \(\phi\)

TENSILE_EQPS

tensile equivalent plastic strain, \(\bar{\varepsilon}^{p}_{t}\)

DAMAGE

damage, \(\phi\)

VOID_COUNT

void count, \(\eta\)

VOID_SIZE

void size, \(\upsilon\)

DAMAGE_DOT

damage rate, \(\dot{\phi}\)

VOID_COUNT_DOT

void count rate, \(\dot{\eta}\)

PLASTIC_WORK_HEAT_RATE

plastic work heat rate, \(\dot{Q}^p\)

5.2.15. Hill Plasticity Model

BEGIN PARAMETERS FOR MODEL HILL_PLASTICITY
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Material coordinates system definition
  #
  COORDINATE SYSTEM             = <string> coordinate_system_name
  DIRECTION FOR ROTATION        = <real> 1|2|3
  ALPHA                         = <real> (degrees)
  SECOND DIRECTION FOR ROTATION = <real> 1|2|3
  SECOND ALPHA                  = <real> (degrees)
  #
  # Yield surface parameters
  #
  YIELD STRESS = <real>
  R11 = <real> (1.0)
  R22 = <real> (1.0)
  R33 = <real> (1.0)
  R12 = <real> (1.0)
  R23 = <real> (1.0)
  R31 = <real> (1.0)
  #
  # Hardening model
  #
  HARDENING MODEL = LINEAR | POWER_LAW | VOCE | USER_DEFINED |
    FLOW_STRESS | DECOUPLED_FLOW_STRESS | JOHNSON_COOK |
    POWER_LAW_BREAKDOWN
  #
  # Linear hardening
  #
  HARDENING MODULUS = <real>
  #
  # Power-law hardening
  #
  HARDENING CONSTANT = <real>
  HARDENING EXPONENT = <real> (0.5)
  LUDERS STRAIN      = <real> (0.0)
  #
  # Voce hardening
  #
  HARDENING MODULUS       = <real>
  EXPONENTIAL COEFFICIENT = <real>
  #
  # Johnson-Cook hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  RATE CONSTANT      = <real>
  REFERENCE RATE     = <real>
  #
  # Power law breakdown hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  RATE COEFFICIENT   = <real>
  RATE EXPONENT      = <real>
  # User defined hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  #
  #
  # Following Commands Pertain to Flow_Stress Hardening Model
  #
  #    -  Isotropic Hardening model
  #
  ISOTROPIC HARDENING MODEL = LINEAR | POWER_LAW | VOCE |
                              USER_DEFINED
  #
  # Specifications for Linear, Power-law, and Voce same as above
  #
  # User defined hardening
  #
  ISOTROPIC HARDENING FUNCTION = <string>iso_hardening_fun_name
  #
  #     - Rate dependence
  #
  RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
     USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  # Specifications for Johnson-Cook, Power-law-breakdown
  #     same as before EXCEPT no need to specify a
  #     hardening function
  #
  # User defined rate multiplier
  #
  RATE MULTIPLIER FUNCTION = <string> rate_mult_function_name
  #
  #     - Temperature dependence
  #
  TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
     TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #  Johnson-Cook temperature dependence
  #
  MELTING TEMPERATURE   = <real>
  REFERENCE TEMPERATURE = <real>
  TEMPERATURE EXPONENT  = <real>
  #
  #  User-defined temperature dependence
  TEMPERATURE MULTIPLIER FUNCTION = <string>temp_mult_function_name
  #
  # Following Commands Pertain to Decoupled_Flow_Stress Hardening Model
  #
  #    -  Isotropic Hardening model
  #
  ISOTROPIC HARDENING MODEL = LINEAR | POWER_LAW | VOCE | USER_DEFINED
  #
  # Specifications for Linear, Power-law, and Voce same as above
  #
  # User defined hardening
  #
  ISOTROPIC HARDENING FUNCTION = <string>isotropic_hardening_function_name
  #
  #     - Rate dependence
  #
  YIELD RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
              USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  # Specifications for Johnson-Cook, Power-law-breakdown same as before
  #     EXCEPT no need to specify a hardening function
  #     AND should be preceded by YIELD
  #
  #     As an example for Johnson-Cook yield rate dependence,
  #
  YIELD RATE CONSTANT  = <real>
  YIELD REFERENCE RATE = <real>
  #
  # User defined rate multiplier
  #
  YIELD RATE MULTIPLIER FUNCTION = <string>yield_rate_mult_function_name
  #
  HARDENING_RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
              USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  #     Syntax same as for yield parameters but with a HARDENING prefix
  #
  #     - Temperature dependence
  #
  YIELD TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
            TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #  Johnson-Cook temperature dependence
  #
  YIELD MELTING TEMPERATURE   = <real>
  YIELD REFERENCE TEMPERATURE = <real>
  YIELD TEMPERATURE EXPONENT  = <real>
  #
  #  User-defined temperature dependence
  YIELD TEMPERATURE MULTIPLIER FUNCTION = <string>yield_temp_mult_fun_name
  #
  HARDENING TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
            TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #   Syntax for hardening constants same as for yield but
  #            with HARDENING prefix
  #
  # Optional Failure Definitions
  #    Following only need to be defined if intend to use failure model
  #
  FAILURE MODEL = TEARING_PARAMETER | JOHNSON_COOK_FAILURE | WILKINS
                  | MODULAR_FAILURE | MODULAR_BCJ_FAILURE

  CRITICAL FAILURE PARAMETER = <real>
  #
  # TEARING_PARAMETER Failure model definitions
  #
  TEARING PARAMETER EXPONENT = <real>
  #
  # JOHNSON_COOK_FAILURE Failure model definitions
  #
  JOHNSON COOK D1       = <real>
  JOHNSON COOK D2       = <real>
  JOHNSON COOK D3       = <real>
  JOHNSON COOK D4       = <real>
  JOHNSON COOK D5       = <real>
  #
  #Following Johnson-Cook parameters can only be defined once.  As such, only
  #  needed if not previously defined via Johnson-Cook multipliers
  #  w/ flow-stress hardening.  Does need to be defined
  #  w/ Decoupled Flow Stress
  #
  REFERENCE RATE        = <real>
  REFERENCE TEMPERATURE = <real>
  MELTING TEMPERATURE   = <real>
  #
  # WILKINS Failure model definitions
  #
  WILKINS ALPHA    = <real>
  WILKINS BETA     = <real>
  WILKINS PRESSURE = <real>
  #
  #  MODULAR_FAILURE Failure model definitions
  #
  PRESSURE MULTIPLIER         = PRESSURE_INDEPENDENT | WILKINS
                                | USER_DEFINED (PRESSURE_INDEPENDENT)
  LODE ANGLE MULTIPLIER       = LODE_ANGLE_INDEPENDENT |
                                WILKINS (LODE_ANGLE_INDEPENDENT)
  TRIAXIALITY MULTIPLIER      = TRIAXIALITY_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (TRIAXIALITY_INDEPENDENT)
  RATE FAIL MULTIPLIER        = RATE_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (RATE_INDEPENDENT)
  TEMPERATURE FAIL MULTIPLIER = TEMPERATURE_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (TEMPERATURE_INDEPENDENT)
  #
  # Individual multiplier definitions
  #
  PRESSURE MULTIPLIER = WILKINS
  WILKINS ALPHA       = <real>
  WILKINS PRESSURE    = <real>
  #
  PRESSURE MULTIPLIER = USER_DEFINED
  PRESSURE MULTIPLIER FUNCTION = <string> pressure_multiplier_fun_name
  #
  LODE ANGLE MULTIPLIER = WILKINS
  WILKINS BETA          = <real>
  #
  TRIAXIALITY MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D1        = <real>
  JOHNSON COOK D2        = <real>
  JOHNSON COOK D3        = <real>
  #
  TRIAXIALITY MULTIPLIER = USER_DEFINED
  TRIAXIALITY MULTIPLIER FUNCTION = <string> triaxiality_multiplier_fun_name
  #
  RATE FAIL MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D4      = <real>
  # REFERENCE RATE should only be added if not previously defined
  REFERENCE RATE       = <real>
  #
  RATE FAIL MULTIPLIER = USER_DEFINED
  RATE FAIL MULTIPLIER FUNCTION = <string> rate_fail_multiplier_fun_name
  #
  TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D5             = <real>
  # JC Temperatures should only be defined if not previously given
  REFERENCE TEMPERATURE       = <real>
  MELTING TEMPERATURE         = <real>
  #
  TEMPERATURE FAIL MULTIPLIER          = USER_DEFINED
  TEMPERATURE FAIL MULTIPLIER FUNCTION = <string> temp_multiplier_fun_name
  #
  # MODULAR BCJ_FAILURE Failure model definitions
  #
  INITIAL DAMAGE    = <real>
  INITIAL VOID SIZE = <real>
  DAMAGE BETA       = <real> (0.5)
  GROWTH MODEL      = COCKS_ASHBY | NO_GROWTH (NO_GROWTH)
  NUCLEATION MODEL  = HORSTEMEYER_GOKHALE | CHU_NEEDLEMAN_STRAIN
                      | NO_NUCLEATION (NO_NUCLEATION)
  #
  GROWTH RATE FAIL MULTIPLIER        = JOHNSON_COOK | USER_DEFINED
                                       | RATE_INDEPENDENT
                                       (RATE_INDEPENDENT)
  GROWTH TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK | USER_DEFINED
                                       | TEMPERATURE_INDEPENDENT
                                       (TEMPERATURE_INDEPENDENT)
  #
  NUCLEATION RATE FAIL MULTIPLIER        = JOHNSON_COOK | USER_DEFINED
                                           | RATE_INDEPENDENT
                                           (RATE_INDEPENDENT)
  NUCLEATION TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK | USER_DEFINED
                                           | TEMPERATURE_INDEPENDENT
                                           (TEMPERATURE_INDEPENDENT)
  #
  # Definitions for individual growth and nucleation models
  #
  GROWTH MODEL = COCKS_ASHBY
  DAMAGE EXPONENT = <real> (0.5)
  #
  NUCLEATION MODEL      = HORSTEMEYER_GOKHALE
  NUCLEATION PARAMETER1 = <real> (0.0)
  NUCLEATION PARAMETER2 = <real> (0.0)
  NUCLEATION PARAMETER3 = <real> (0.0)
  #
  NUCLEATION MODEL          = CHU_NEEDLEMAN_STRAIN
  NUCLEATION AMPLITUDE      = <real>
  MEAN NUCLEATION STRAIN    = <real>
  NUCLEATION STRAIN STD DEV = <real>
  #
  # Definitions for rate and temperature fail multiplier
  #   Note: only showing definitions for growth.
  #    Nucleation terms are the same just with NUCLEATION instead
  #    of GROWTH
  #
  GROWTH RATE FAIL MULTIPLIER = JOHNSON_COOK
  GROWTH JOHNSON COOK D4      = <real>
  GROWTH REFERENCE RATE       = <real>
  #
  GROWTH RATE FAIL MULTIPLIER          = USER_DEFINED
  GROWTH RATE FAIL MULTIPLIER FUNCTION = <string> growth_rate_fail_mult_func
  #
  GROWTH TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK
  GROWTH JOHNSON COOK D5             = <real>
  GROWTH REFERENCE TEMPERATURE       = <real>
  GROWTH MELTING TEMPERATURE         = <real>
  #
  GROWTH TEMPERATURE FAIL MULTIPLIER          = USER_DEFINED
  GROWTH TEMPERATURE FAIL MULTIPLIER FUNCTION = <string> temp_fail_mult_func
  #
  #
  # Optional Adiabatic Heating/Thermal Softening  Definitions
  #    Following only need to be defined if intend to use failure model
  #
  THERMAL SOFTENING MODEL = ADIABATIC | COUPLED
  #
  SPECIFIC HEAT = <real> #not needed for COUPLED
  BETA_TQ       = <real>
END [PARAMETERS FOR MODEL HILL_PLASTICITY]

The Hill plasticity model is similar to other plasticity models except that it is not isotropic. It is a hypoelastic, rate-independent plasticity model. The rate form of the equation assumes an additive split of the rate of deformation into an elastic and plastic part

\[D_{ij} = D_{ij}^{\text{e}} + D_{ij}^{\text{p}}\]

The stress rate only depends on the elastic rate of deformation

\[\stackrel{\circ}{\sigma}_{ij} = \mathbb{C}_{ijkl}D_{kl}^{\text{e}}\]

where \(\mathbb{C}_{ijkl}\) are the components of the fourth-order, isotropic elasticity tensor.

The Hill plasticity model has an orthotropic yield surface that assumes orthogonal principal material directions. An example of this yield surface is presented below in Fig. 5.8 along with examples of two isotropic surfaces – the von Mises (\(J_2\)) and Hosford (with \(a=8\)). The various surface parameters correspond to 2090-T3 aluminum and the specific Hill strengths are found in [[15]]. By comparing the Hill surface to the two isotropic surfaces, the impact of the anisotropy is clear. Additionally, substantial differences to the normals of the yield surfaces at points of intersection highlight the impact of the yield function selection on the resulting flow directions.

Like other plasticity models, the Hill yield surface, \(f\), is written,

\[f\left(\sigma_{ij},\bar{\varepsilon}^p\right)=\phi\left(\sigma_{ij}\right)-\bar{\sigma}\left(\bar{\varepsilon}^p\right)=0,\]

with \(\phi\) being the effective stress and \(\bar{\sigma}\) is the current yield stress that may be dependent on rate and/or temperature. The Hill effective stress is essentially an orthotropic extension of the von Mises function. After accounting for plastic incompressibility and related constraints, there are six individual yield stresses: \(\sigma^{y}_{11}\), \(\sigma^{y}_{22}\), \(\sigma^{y}_{33}\), \(\tau^{y}_{12}\), \(\tau^{y}_{23}\), and \(\tau^{y}_{31}\). These yield stresses correspond to 3 normal and 3 shear yield stresses. Written in terms of the components, the effective stress has the form,

(5.21)\[\begin{split}\phi^{2}\left( \sigma_{ij} \right) & = F \left( \hat\sigma_{22} - \hat\sigma_{33} \right)^{2} + G \left( \hat\sigma_{33} - \hat\sigma_{11} \right)^{2} + H \left( \hat\sigma_{11} - \hat\sigma_{22} \right)^{2} \nonumber \\ & + 2L \hat\sigma_{23}^{2} + 2M \hat\sigma_{31}^{2} + 2N \hat\sigma_{12}^{2}. \nonumber\end{split}\]
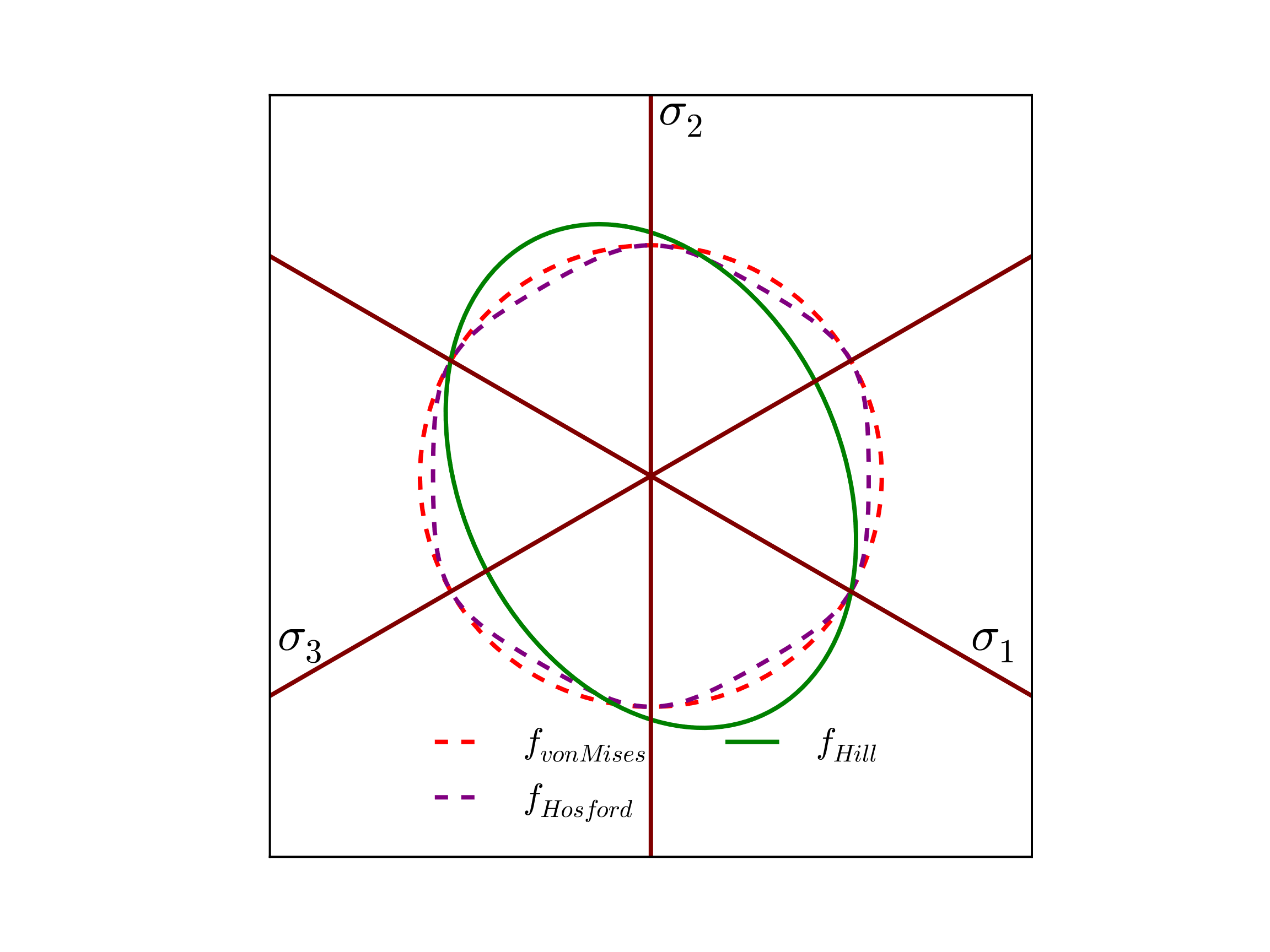
../../_images/hillSurface.png

Fig. 5.8 Example anisotropic Hill yield surface, \(f_{Hill}\left(\sigma_{ij},\bar{\varepsilon}^p=0\right)\), presented in the deviatoric \(\pi\)-plane fit to 2090-T3 aluminum. Comparison von Mises (\(J_2\)) and Hosford (with \(a=8\)) surfaces are also presented.

The coefficients \(F\), \(G\), \(H\), \(L\), \(M\), and \(N\) were introduced by Hill. In terms of the yield stresses they are:

\[F = \frac{\left(\bar{\sigma}\right)^{2}}{2}\left[ \frac{1}{\left( \sigma_{22}^{y} \right)^{2}} + \frac{1}{\left( \sigma_{33}^{y} \right)^{2}} - \frac{1}{\left( \sigma_{11}^{y} \right)^{2}}\right] \;\;\; ; \;\;\; L = \frac{\left(\bar{\sigma}\right)^{2}}{2} \left[ \frac{1}{\left(\tau_{23}^{y}\right)^{2}} \right]\]
(5.22)\[G = \frac{\left(\bar{\sigma}\right)^{2}}{2}\left[ \frac{1}{\left( \sigma_{33}^{y} \right)^{2}} + \frac{1}{\left( \sigma_{11}^{y} \right)^{2}} - \frac{1}{\left( \sigma_{22}^{y} \right)^{2}} \right] \;\;\; ; \;\;\; M = \frac{\left(\bar{\sigma}\right)^{2}}{2} \left[ \frac{1}{\left(\tau_{31}^{y}\right)^{2}} \right]\]
\[H = \frac{\left(\bar{\sigma}\right)^{2}}{2}\left[ \frac{1}{\left( \sigma_{11}^{y} \right)^{2}} + \frac{1}{\left( \sigma_{22}^{y} \right)^{2}} - \frac{1}{\left( \sigma_{33}^{y} \right)^{2}} \right] \;\;\; ; \;\;\; N = \frac{\left(\bar{\sigma}\right)^{2}}{2} \left[ \frac{1}{\left(\tau_{12}^{y}\right)^{2}} \right].\]

where \(\bar{\sigma}\) is a reference yield stress.

Rather than input the six independent yield stresses, the ratios of the yield stresses to some reference yield stress are generally used as input. These ratios are

\[R_{11} = \frac{\sigma^{y}_{11}}{\bar{\sigma}} \;\;\; ; \;\;\; R_{12} = \sqrt{3}\frac{\tau^{y}_{12}}{\bar{\sigma}}\]
(5.23)\[R_{22} = \frac{\sigma^{y}_{22}}{\bar{\sigma}} \;\;\; ; \;\;\; R_{23} = \sqrt{3}\frac{\tau^{y}_{23}}{\bar{\sigma}}\]
\[R_{33} = \frac{\sigma^{y}_{33}}{\bar{\sigma}} \;\;\; ; \;\;\; R_{31} = \sqrt{3}\frac{\tau^{y}_{31}}{\bar{\sigma}}.\]

These ratios are set up so that if \(R_{ij} = 1\) then the yield surface is isotropic.

The orientation of the principal material axes with respect to the global Cartesian axes may be specified by the user. First, a rectangular or cylindrical reference coordinate system is defined. Spherical coordinate systems are not currently implemented for the Hill model. The material coordinate system can then be defined through two successive rotations about axes in the reference rectangular or cylindrical coordinate system. In the case of the cylindrical coordinate system this allows the principal material axes to vary point-wise in a given element block. Refer to Section 5.1.7 for details on the definition of material coordinate systems.

The plastic rate of deformation, as with the isotropic models, assumes associated flow

\[D_{ij}^{\text{p}} = \dot{\gamma} \frac{\partial\phi}{\partial\sigma_{ij}}.\]

Given the form for \(\phi\), the consistency parameter, \(\dot\gamma\) is equal to the rate of the equivalent plastic strain, \(\dot{\bar{\varepsilon}}^{p}\).

For more information about the Hill plasticity model, consult [[16]]. Additional discussion on options for failure models and adiabatic heating may be found in [[10], [11]] and [[12]], respectively.

In the command blocks that define the Hill plasticity model:

  • See Section 5.1.5 for more information on elastic constants input.

  • See Section 5.1.7 for more information on material coordinates system definition commands.

  • The reference nominal yield stress, \(\bar{\sigma}\), is defined with the YIELD STRESS command line.

  • The ratio of the normal yield stress in the \(\bar{\bf e}_{1}\bar{\bf e}_{1}\) material direction is defined with the R11 command line. The default is 1.0.

  • The ratio of the normal yield stress in the \(\bar{\bf e}_{2}\bar{\bf e}_{2}\) material direction is defined with the R22 command line. The default is 1.0.

  • The ratio of the normal yield stress in the \(\bar{\bf e}_{3}\bar{\bf e}_{3}\) material direction is defined with the R33 command line. The default is 1.0.

  • The ratio of the shear yield stress in the \(\bar{\bf e}_{1}\bar{\bf e}_{2}\) material direction is defined with the R12 command line. The default is 1.0.

  • The ratio of the shear yield stress in the \(\bar{\bf e}_{2}\bar{\bf e}_{3}\) material direction is defined with the R23 command line. The default is 1.0.

  • The ratio of the shear yield stress in the \(\bar{\bf e}_{3}\bar{\bf e}_{1}\) material direction is defined with the R31 command line. The default is 1.0.

  • The type of hardening law is defined with the HARDENING MODEL command line, other hardening commands then define the specific shape of that hardening curve.

  • The hardening modulus for a linear hardening model is defined with the HARDENING MODULUS command line.

  • The hardening constant for a power law hardening model is defined with the HARDENING CONSTANT command line.

  • The hardening exponent for a power law hardening model is defined with the HARDENING EXPONENT command line.

  • The L"{u}ders strain for a power law hardening model is defined with the LUDERS STRAIN command line.

  • The hardening function for a user defined hardening model is defined with the HARDENING FUNCTION command line.

  • The shape of the spline for the spline based hardening is defined by the CUBIC SPLINE TYPE, CARDINAL PARAMETER, KNOT EQPS, and KNOT STRESS command lines.

Output variables available for this model are listed in Table 5.13.

Table 5.13 State Variables for HILL PLASTICITY Model (Section 5.2.15)

Name

Description

EQPS

equivalent plastic strain, \(\bar{\varepsilon}^{p}\)

EQDOT

equivalent plastic strain rate, \(\dot{\bar{\varepsilon}}^{p}\)

SEFF

effective stress, \(\phi\)

TENSILE_EQPS

tensile equivalent plastic strain, \(\bar{\varepsilon}^{p}_{t}\)

DAMAGE

damage, \(\phi\)

VOID_COUNT

void count, \(\eta\)

VOID_SIZE

void size, \(\upsilon\)

DAMAGE_DOT

damage rate, \(\dot{\phi}\)

VOID_COUNT_DOT

void count rate, \(\dot{\eta}\)

PLASTIC_WORK_HEAT_RATE

plastic work heat rate, \(\dot{Q}^p\)

5.2.16. Barlat Plasticity Model

BEGIN PARAMETERS FOR MODEL BARLAT_PLASTICITY
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Material coordinates system definition
  #
  COORDINATE SYSTEM             = <string> coordinate_system_name
  DIRECTION FOR ROTATION        = <real> 1|2|3
  ALPHA                         = <real> (degrees)
  SECOND DIRECTION FOR ROTATION = <real> 1|2|3
  SECOND ALPHA                  = <real> (degrees)
  #
  # Yield surface parameters
  #
  YIELD STRESS = <real>
  A            = <real> (4.0)
  CP12         = <real> (1.0)
  CP13         = <real> (1.0)
  CP21         = <real> (1.0)
  CP23         = <real> (1.0)
  CP31         = <real> (1.0)
  CP32         = <real> (1.0)
  CP44         = <real> (1.0)
  CP55         = <real> (1.0)
  CP66         = <real> (1.0)
  CPP12        = <real> (1.0)
  CPP13        = <real> (1.0)
  CPP21        = <real> (1.0)
  CPP23        = <real> (1.0)
  CPP31        = <real> (1.0)
  CPP32        = <real> (1.0)
  CPP44        = <real> (1.0)
  CPP55        = <real> (1.0)
  CPP66        = <real> (1.0)
  #
  # Hardening model
  #
  HARDENING MODEL = LINEAR | POWER_LAW | VOCE | USER_DEFINED |
    FLOW_STRESS | DECOUPLED_FLOW_STRESS | JOHNSON_COOK |
    POWER_LAW_BREAKDOWN
  #
  # Linear hardening
  #
  HARDENING MODULUS = <real>
  #
  # Power-law hardening
  #
  HARDENING CONSTANT = <real>
  HARDENING EXPONENT = <real> (0.5)
  LUDERS STRAIN      = <real> (0.0)
  #
  # Voce hardening
  #
  HARDENING MODULUS       = <real>
  EXPONENTIAL COEFFICIENT = <real>
  #
  # Johnson-Cook hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  RATE CONSTANT      = <real>
  REFERENCE RATE     = <real>
  #
  # Power law breakdown hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  RATE COEFFICIENT   = <real>
  RATE EXPONENT      = <real>
  # User defined hardening
  #
  HARDENING FUNCTION = <string>hardening_function_name
  #
  #
  # Following Commands Pertain to Flow_Stress Hardening Model
  #
  #    -  Isotropic Hardening model
  #
  ISOTROPIC HARDENING MODEL = LINEAR | POWER_LAW | VOCE |
                              USER_DEFINED
  #
  # Specifications for Linear, Power-law, and Voce same as above
  #
  # User defined hardening
  #
  ISOTROPIC HARDENING FUNCTION = <string>iso_hardening_fun_name
  #
  #     - Rate dependence
  #
  RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
     USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  # Specifications for Johnson-Cook, Power-law-breakdown
  #     same as before EXCEPT no need to specify a
  #     hardening function
  #
  # User defined rate multiplier
  #
  RATE MULTIPLIER FUNCTION = <string> rate_mult_function_name
  #
  #     - Temperature dependence
  #
  TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
     TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #  Johnson-Cook temperature dependence
  #
  MELTING TEMPERATURE   = <real>
  REFERENCE TEMPERATURE = <real>
  TEMPERATURE EXPONENT  = <real>
  #
  #  User-defined temperature dependence
  TEMPERATURE MULTIPLIER FUNCTION = <string>temp_mult_function_name
  #
  # Following Commands Pertain to Decoupled_Flow_Stress Hardening Model
  #
  #    -  Isotropic Hardening model
  #
  ISOTROPIC HARDENING MODEL = LINEAR | POWER_LAW | VOCE | USER_DEFINED
  #
  # Specifications for Linear, Power-law, and Voce same as above
  #
  # User defined hardening
  #
  ISOTROPIC HARDENING FUNCTION = <string>isotropic_hardening_function_name
  #
  #     - Rate dependence
  #
  YIELD RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
              USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  # Specifications for Johnson-Cook, Power-law-breakdown same as before
  #     EXCEPT no need to specify a hardening function
  #     AND should be preceded by YIELD
  #
  #     As an example for Johnson-Cook yield rate dependence,
  #
  YIELD RATE CONSTANT  = <real>
  YIELD REFERENCE RATE = <real>
  #
  # User defined rate multiplier
  #
  YIELD RATE MULTIPLIER FUNCTION = <string>yield_rate_mult_function_name
  #
  HARDENING_RATE MULTIPLIER = JOHNSON_COOK | POWER_LAW_BREAKDOWN |
              USER_DEFINED | RATE_INDEPENDENT (RATE_INDEPENDENT)
  #
  #     Syntax same as for yield parameters but with a HARDENING prefix
  #
  #     - Temperature dependence
  #
  YIELD TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
            TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #  Johnson-Cook temperature dependence
  #
  YIELD MELTING TEMPERATURE   = <real>
  YIELD REFERENCE TEMPERATURE = <real>
  YIELD TEMPERATURE EXPONENT  = <real>
  #
  #  User-defined temperature dependence
  YIELD TEMPERATURE MULTIPLIER FUNCTION = <string>yield_temp_mult_fun_name
  #
  HARDENING TEMPERATURE MULTIPLIER = JOHNSON_COOK | USER_DEFINED |
            TEMPERATURE_INDEPENDENT (TEMPERATURE_INDEPENDENT)
  #
  #   Syntax for hardening constants same as for yield but
  #            with HARDENING prefix
  #
  # Optional Failure Definitions
  #    Following only need to be defined if intend to use failure model
  #
  FAILURE MODEL = TEARING_PARAMETER | JOHNSON_COOK_FAILURE | WILKINS
                  | MODULAR_FAILURE | MODULAR_BCJ_FAILURE

  CRITICAL FAILURE PARAMETER = <real>
  #
  # TEARING_PARAMETER Failure model definitions
  #
  TEARING PARAMETER EXPONENT = <real>
  #
  # JOHNSON_COOK_FAILURE Failure model definitions
  #
  JOHNSON COOK D1       = <real>
  JOHNSON COOK D2       = <real>
  JOHNSON COOK D3       = <real>
  JOHNSON COOK D4       = <real>
  JOHNSON COOK D5       = <real>
  #
  #Following Johnson-Cook parameters can only be defined once.  As such, only
  #  needed if not previously defined via Johnson-Cook multipliers
  #  w/ flow-stress hardening.  Does need to be defined
  #  w/ Decoupled Flow Stress
  #
  REFERENCE RATE        = <real>
  REFERENCE TEMPERATURE = <real>
  MELTING TEMPERATURE   = <real>
  #
  # WILKINS Failure model definitions
  #
  WILKINS ALPHA    = <real>
  WILKINS BETA     = <real>
  WILKINS PRESSURE = <real>
  #
  #  MODULAR_FAILURE Failure model definitions
  #
  PRESSURE MULTIPLIER         = PRESSURE_INDEPENDENT | WILKINS
                                | USER_DEFINED (PRESSURE_INDEPENDENT)
  LODE ANGLE MULTIPLIER       = LODE_ANGLE_INDEPENDENT |
                                WILKINS (LODE_ANGLE_INDEPENDENT)
  TRIAXIALITY MULTIPLIER      = TRIAXIALITY_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (TRIAXIALITY_INDEPENDENT)
  RATE FAIL MULTIPLIER        = RATE_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (RATE_INDEPENDENT)
  TEMPERATURE FAIL MULTIPLIER = TEMPERATURE_INDEPENDENT | JOHNSON_COOK
                                | USER_DEFINED (TEMPERATURE_INDEPENDENT)
  #
  # Individual multiplier definitions
  #
  PRESSURE MULTIPLIER = WILKINS
  WILKINS ALPHA       = <real>
  WILKINS PRESSURE    = <real>
  #
  PRESSURE MULTIPLIER = USER_DEFINED
  PRESSURE MULTIPLIER FUNCTION = <string> pressure_multiplier_fun_name
  #
  LODE ANGLE MULTIPLIER = WILKINS
  WILKINS BETA          = <real>
  #
  TRIAXIALITY MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D1        = <real>
  JOHNSON COOK D2        = <real>
  JOHNSON COOK D3        = <real>
  #
  TRIAXIALITY MULTIPLIER = USER_DEFINED
  TRIAXIALITY MULTIPLIER FUNCTION = <string> triaxiality_multiplier_fun_name
  #
  RATE FAIL MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D4      = <real>
  # REFERENCE RATE should only be added if not previously defined
  REFERENCE RATE       = <real>
  #
  RATE FAIL MULTIPLIER = USER_DEFINED
  RATE FAIL MULTIPLIER FUNCTION = <string> rate_fail_multiplier_fun_name
  #
  TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK
  JOHNSON COOK D5             = <real>
  # JC Temperatures should only be defined if not previously given
  REFERENCE TEMPERATURE       = <real>
  MELTING TEMPERATURE         = <real>
  #
  TEMPERATURE FAIL MULTIPLIER          = USER_DEFINED
  TEMPERATURE FAIL MULTIPLIER FUNCTION = <string> temp_multiplier_fun_name
  #
  # MODULAR BCJ_FAILURE Failure model definitions
  #
  INITIAL DAMAGE    = <real>
  INITIAL VOID SIZE = <real>
  DAMAGE BETA       = <real> (0.5)
  GROWTH MODEL      = COCKS_ASHBY | NO_GROWTH (NO_GROWTH)
  NUCLEATION MODEL  = HORSTEMEYER_GOKHALE | CHU_NEEDLEMAN_STRAIN
                      | NO_NUCLEATION (NO_NUCLEATION)
  #
  GROWTH RATE FAIL MULTIPLIER        = JOHNSON_COOK | USER_DEFINED
                                       | RATE_INDEPENDENT
                                       (RATE_INDEPENDENT)
  GROWTH TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK | USER_DEFINED
                                       | TEMPERATURE_INDEPENDENT
                                       (TEMPERATURE_INDEPENDENT)
  #
  NUCLEATION RATE FAIL MULTIPLIER        = JOHNSON_COOK | USER_DEFINED
                                           | RATE_INDEPENDENT
                                           (RATE_INDEPENDENT)
  NUCLEATION TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK | USER_DEFINED
                                           | TEMPERATURE_INDEPENDENT
                                           (TEMPERATURE_INDEPENDENT)
  #
  # Definitions for individual growth and nucleation models
  #
  GROWTH MODEL = COCKS_ASHBY
  DAMAGE EXPONENT = <real> (0.5)
  #
  NUCLEATION MODEL      = HORSTEMEYER_GOKHALE
  NUCLEATION PARAMETER1 = <real> (0.0)
  NUCLEATION PARAMETER2 = <real> (0.0)
  NUCLEATION PARAMETER3 = <real> (0.0)
  #
  NUCLEATION MODEL          = CHU_NEEDLEMAN_STRAIN
  NUCLEATION AMPLITUDE      = <real>
  MEAN NUCLEATION STRAIN    = <real>
  NUCLEATION STRAIN STD DEV = <real>
  #
  # Definitions for rate and temperature fail multiplier
  #   Note: only showing definitions for growth.
  #    Nucleation terms are the same just with NUCLEATION instead
  #    of GROWTH
  #
  GROWTH RATE FAIL MULTIPLIER = JOHNSON_COOK
  GROWTH JOHNSON COOK D4      = <real>
  GROWTH REFERENCE RATE       = <real>
  #
  GROWTH RATE FAIL MULTIPLIER          = USER_DEFINED
  GROWTH RATE FAIL MULTIPLIER FUNCTION = <string> growth_rate_fail_mult_func
  #
  GROWTH TEMPERATURE FAIL MULTIPLIER = JOHNSON_COOK
  GROWTH JOHNSON COOK D5             = <real>
  GROWTH REFERENCE TEMPERATURE       = <real>
  GROWTH MELTING TEMPERATURE         = <real>
  #
  GROWTH TEMPERATURE FAIL MULTIPLIER          = USER_DEFINED
  GROWTH TEMPERATURE FAIL MULTIPLIER FUNCTION = <string> temp_fail_mult_func
  #
  #
  # Optional Adiabatic Heating/Thermal Softening  Definitions
  #    Following only need to be defined if intend to use failure model
  #
  THERMAL SOFTENING MODEL = ADIABATIC | COUPLED
  #
  SPECIFIC HEAT = <real> #not needed for COUPLED
  BETA_TQ       = <real>
END [PARAMETERS FOR MODEL BARLAT_PLASTICITY]

The Barlat plasticity model is a hypoelastic, rate-independent plasticity model. The underlying yield surface is both anisotropic and non-quadratic [[17]]. With respect to the former, linear transformations of the deviatoric stress are used to capture texture and anisotropy effects. The rate form of this model assumes an additive split of the rate of deformation into an elastic and plastic part

\[D_{ij} = D_{ij}^{\text{e}} + D_{ij}^{\text{p}}.\]

The stress rate only depends on the elastic rate of deformation

\[\stackrel{\circ}{\sigma}_{ij} = \mathbb{C}_{ijkl}D_{kl}^{\text{e}}\]

where \(\mathbb{C}_{ijkl}\) are the components of the fourth-order, isotropic elasticity tensor.

To describe anisotropy in the yield-behavior, two linear transformation tensors, \(C^{\prime}_{ijkl}\) and \(C^{\prime\prime}_{ijkl}\), are introduced such that,

\[s_{ij}^{\prime}=C^{\prime}_{ijkl}s_{kl} \qquad ; \qquad s_{ij}^{\prime\prime}=C^{\prime\prime}_{ijkl}s_{kl},\]

with \(s_{ij}\) being the deviatoric stress tensor (\(s_{ij}=\sigma_{ij}-1/3\sigma_{kk}\delta_{ij}\)) and \(s_{ij}^{\prime}\) and \(s_{ij}^{\prime\prime}\) being transformed stresses. Two transformations are used to capture both the anisotropy of the yield surface and flow rule. In Voigt notation the two transformation tensors are given as,

\[\begin{split}\left[C^{\prime}\right] = \left[\begin{array}{cccccc} 0 & -c_{12}^{\prime} & -c_{13}^{\prime} & 0 & 0 & 0 \\ -c_{21}^{\prime} & 0 & -c_{23}^{\prime} & 0 & 0 & 0 \\ -c_{31}^{\prime} & -c_{32}^{\prime} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & c_{44}^{\prime} & 0 & 0 \\ 0 & 0 & 0 & 0 & c_{55}^{\prime} & 0 \\ 0 & 0 & 0 & 0 & 0 & c_{66}^{\prime} \end{array}\right]\end{split}\]
\[\begin{split}\left[C^{\prime\prime}\right] = \left[\begin{array}{cccccc} 0 & -c_{12}^{\prime\prime} & -c_{13}^{\prime\prime} & 0 & 0 & 0 \\ -c_{21}^{\prime\prime} & 0 & -c_{23}^{\prime\prime} & 0 & 0 & 0 \\ -c_{31}^{\prime\prime} & -c_{32}^{\prime\prime} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & c_{44}^{\prime\prime} & 0 & 0 \\ 0 & 0 & 0 & 0 & c_{55}^{\prime\prime} & 0 \\ 0 & 0 & 0 & 0 & 0 & c_{66}^{\prime\prime} \end{array}\right] .\end{split}\]

Alternatively, the transformed stresses may be written in terms of the Cauchy stress tensor as,

\[s_{ij}^{\prime}=L^{\prime}_{ijkl}\sigma_{kl} \qquad ; \qquad s^{\prime\prime}_{ij}=L^{\prime\prime}_{ijkl}\sigma_{kl},\]

where \(L^{\prime}_{ijkl}=C^{\prime}_{ijmn}I\!I_{mnkl}\) and \(L^{\prime\prime}_{ijkl}=C^{\prime\prime}_{ijmn}I\!I_{mnkl}\). In this case, \(I\!I_{ijkl}\) is the symmetric deviatoric projection tensor and takes the form of,

\[I\!I_{ijkl}=\frac{1}{2}\left(\delta_{ik}\delta_{jl}+\delta_{il}\delta_{jk}\right)-\frac{1}{3}\delta_{ij}\delta_{kl}.\]

In reduced form,

\[\begin{split}\left[L^{\prime}\right] =\frac{1}{3} \left[\begin{array}{cccccc} c_{12}^{\prime}+c_{13}^{\prime} & -2c_{12}^{\prime}+c_{13}^{\prime} &c_{12}^{\prime}-2c_{13}^{\prime} & 0 & 0 & 0 \\ -2c_{21}^{\prime}+c_{23}^{\prime} & c_{21}^{\prime}+c_{23}^{\prime} & c_{21}^{\prime}-2c_{23}^{\prime} & 0 & 0 & 0 \\ -2c_{31}^{\prime}+c_{32}^{\prime}& c_{31}^{\prime}-2c_{32}^{\prime} & c^{\prime}_{31}+c_{32}^{\prime} & 0 & 0 & 0 \\ 0 & 0 & 0 & 3c_{44}^{\prime} & 0 & 0 \\ 0 & 0 & 0 & 0 & 3c_{55}^{\prime} & 0 \\ 0 & 0 & 0 & 0 & 0 & 3c_{66}^{\prime} \end{array}\right],\end{split}\]

and an analogous expression may be written for \(L^{\prime\prime}_{ijkl}\).

The yield surface, \(f\), is given as,

\[f\left(\sigma_{ij},\bar{\varepsilon}^p\right)=\phi\left(\sigma_{ij}\right)-\bar{\sigma}\left(\bar{\varepsilon}^p\right)=0,\]

in which \(\phi\left(\sigma_{ij}\right)\) is the effective stress and \(\bar{\sigma}\left(\bar{\varepsilon}^p\right)\) is the current yield stress that may depend on rate and/or temperature. The effective stress is written in terms of the principal transformed stresses (\(s^{\prime}_i\) and \(s^{\prime\prime}_i\),respectively) and the yield surface exponent, \(a\), as,

\[\begin{split}\phi\left(\sigma_{ij}\right) = & \bigg\{\frac{1}{4}\Big[ |s^{\prime}_1-s^{\prime\prime}_1|^a+ |s^{\prime}_1-s^{\prime\prime}_2|^a+ |s^{\prime}_1-s^{\prime\prime}_3|^a \nonumber \\ & + |s^{\prime}_2-s^{\prime\prime}_1|^a+ |s^{\prime}_2-s^{\prime\prime}_2|^a+ |s^{\prime}_2-s^{\prime\prime}_3|^a \\ & + |s^{\prime}_3-s^{\prime\prime}_1|^a+ |s^{\prime}_3-s^{\prime\prime}_2|^a+ |s^{\prime}_3-s^{\prime\prime}_3|^a \Big]\bigg\}^{1/a} . \nonumber\end{split}\]

An example of such a yield surface is given in Fig. 5.9 along with examples of previously presented (von Mises, Hosford, Hill) surfaces. The presented Barlat surface corresponds to that of 2090-T3 aluminum first characterized by Barlat et al. [[17]]. In Fig. 5.9, both the anisotropy and non-quadratic nature of the yield surface is evident leading to differing strengths and flow directions at various stresses from any of the other models.

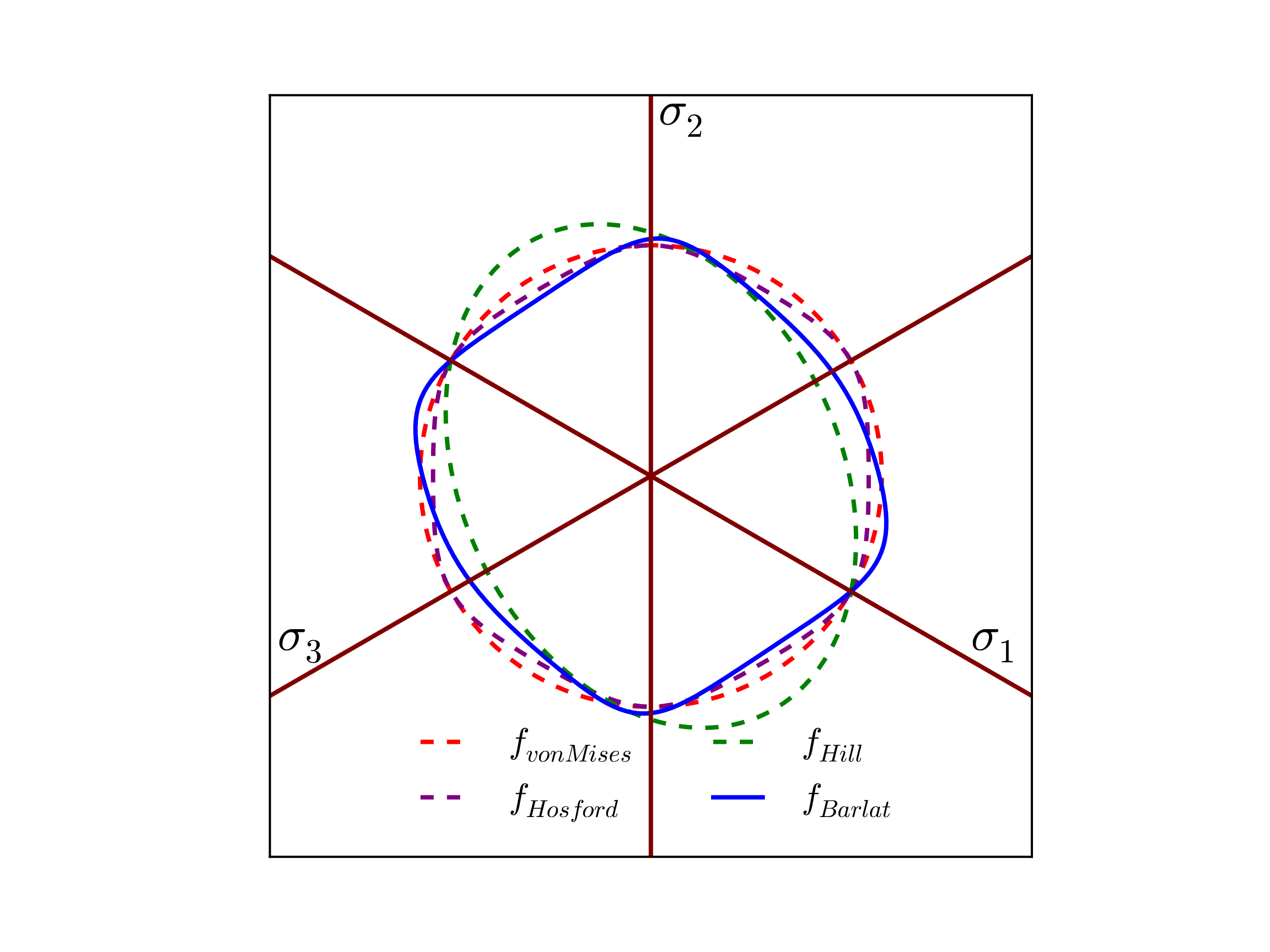
../../_images/barlatSurface.png

Fig. 5.9 Example Barlat yield surface, \(f_{Barlat}\left(\sigma_{ij},\bar{\varepsilon}^p=0\right)\), of 2090-T3 aluminum presented in the deviatoric \(\pi\)-plane. Comparison von Mises (\(J_2\)), Hosford (with \(a=8\)), and Hill surfaces are also presented for comparison.

The orientation of the principal material axes with respect to the global Cartesian axes may be specified by the user. First, a rectangular or cylindrical reference coordinate system is defined. Spherical coordinate systems are not currently implemented for the Barlat model. The material coordinate system can then be defined through two successive rotations about axes in the reference rectangular or cylindrical coordinate system. In the case of the cylindrical coordinate system this allows the principal material axes to vary point-wise in a given element block. Refer to Section 5.1.7 for details on the definition of material coordinate systems.

The plastic rate of deformation, as with the isotropic models, assumes associated flow

\[D_{ij}^{\text{p}} = \dot{\gamma} \frac{\partial\phi}{\partial\sigma_{ij}},\]

in which \(\dot{\gamma}\) is the consistency multiplier. Given the form for \(\phi\), \(\dot\gamma\) is equal to the rate of the equivalent plastic strain, \(\dot{\bar{\varepsilon}}^{p}\). As the yield surface is cast in transformed stress space, determining the flow direction in Cartesian space may be done via the chain rule (details may be found in [[15]]) leading to an expression of the form,

(5.24)\[\frac{\partial\phi}{\partial\sigma_{ij}}=\sum_{k=1}^3\left(\frac{\partial\phi}{\partial s^{\prime}_k} \frac{\partial s^{\prime}_k}{\partial s^{\prime}_{mn}}L^{\prime}_{mnij}+\frac{\partial\phi} {\partial{s^{\prime\prime}_k}}\frac{\partial s^{\prime\prime}_k}{\partial s^{\prime\prime}_{mn}} L^{\prime\prime}_{mnij}\right).\]

For more information about the Barlat plasticity model, consult [[17], [15]]. Additional discussion on options for failure models and adiabatic heating may be found in [[10], [11]] and [[12]], respectively.

In the command blocks that define the Barlat plasticity model:

  • See Section 5.1.5 for more information on elastic constants input.

  • See Section 5.1.7 for more information on material coordinates system definition commands.

  • The reference nominal yield stress, \(\bar{\sigma}\), is defined with the YIELD STRESS command line.

  • The exponent for the yield surface description, \(a\), is defined with the A command line.

  • The transformation coefficient, \(c^{'}_{12}\), is defined with the CP12 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{'}_{13}\), is defined with the CP13 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{'}_{21}\), is defined with the CP21 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{'}_{23}\), is defined with the CP23 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{'}_{31}\), is defined with the CP31 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{'}_{32}\), is defined with the CP32 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{'}_{44}\), is defined with the CP44 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{'}_{55}\), is defined with the CP55 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{'}_{66}\), is defined with the CP66 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{''}_{12}\), is defined with the CPP12 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{''}_{13}\), is defined with the CPP13 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{''}_{21}\), is defined with the CPP21 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{''}_{23}\), is defined with the CPP23 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{''}_{31}\), is defined with the CPP31 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{''}_{32}\), is defined with the CPP32 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{''}_{44}\), is defined with the CPP44 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{''}_{55}\), is defined with the CPP55 command line. It is defaulted to 1.0.

  • The transformation coefficient, \(c^{''}_{66}\), is defined with the CPP66 command line. It is defaulted to 1.0.

  • The type of hardening law is defined with the HARDENING MODEL command line, other hardening commands then define the specific shape of that hardening curve.

  • The hardening modulus for a linear hardening model is defined with the HARDENING MODULUS command line.

  • The hardening constant for a power law hardening model is defined with the HARDENING CONSTANT command line.

  • The hardening exponent for a power law hardening model is defined with the HARDENING EXPONENT command line.

  • The L"{u}ders strain for a power law hardening model is defined with the LUDERS STRAIN command line.

  • The hardening function for a user defined hardening model is defined with the HARDENING FUNCTION command line.

  • The shape of the spline for the spline based hardening is defined by the CUBIC SPLINE TYPE, CARDINAL PARAMETER, KNOT EQPS, and KNOT STRESS command lines.

Output variables available for this model are listed in Table 5.14.

Table 5.14 State Variables for BARLAT PLASTICITY Model (Section 5.2.16)

Name

Description

EQPS

equivalent plastic strain, \(\bar{\varepsilon}^{p}\)

EQDOT

equivalent plastic strain rate, \(\dot{\bar{\varepsilon}}^{p}\)

SEFF

effective stress, \(\phi\)

TENSILE_EQPS

tensile equivalent plastic strain, \(\bar{\varepsilon}^{p}_{t}\)

DAMAGE

damage, \(\phi\)

VOID_COUNT

void count, \(\eta\)

VOID_SIZE

void size, \(\upsilon\)

DAMAGE_DOT

damage rate, \(\dot{\phi}\)

VOID_COUNT_DOT

void count rate, \(\dot{\eta}\)

PLASTIC_WORK_HEAT_RATE

plastic work heat rate, \(\dot{Q}^p\)

5.2.17. Johnson–Cook Model

BEGIN PARAMETERS FOR MODEL JOHNSON_COOK
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Yield surface parameters
  #
  YIELD STRESS = <real>
  HARDENING CONSTANT = <real>hardening_constant
  HARDENING EXPONENT = <real>hardening_exponent
  RHOCV = <real>rho_cv
  RATE CONSTANT = <real>rate_constant
  REFERENCE RATE = <real>reference_rate(0.001)
  D1 = <real>d1(0.0)
  D2 = <real>d2(0.0)
  D3 = <real>d3(0.0)
  D4 = <real>d4(0.0)
  D5 = <real>d5(0.0)
  EDOT_REF = <real>edot_ref(0.0)
  #
  # Temperature softening commands
  #
  BETA = <real>beta(0.95)
  THERMAL EXPONENT = <real>thermal_exponent
  REFERENCE TEMPERATURE = <real>reference_temperature
  MELT TEMPERATURE = <real>melt_temperature
  INITIAL TEMPERATURE = <real>init_temperature
  FORMULATION = <int>form(0)
END [PARAMETERS FOR MODEL JOHNSON_COOK]

The Johnson–Cook model is used to model materials—typically metals—undergoing plastic deformation at high rates and finite strains. The hardening function is rate- and temperature-dependent and is defined by

(5.25)\[\sigma = \left[\sigma_y + B \left(\bar{\varepsilon}_p\right)^{N}\right]\left[1+C\left<\ln\dot\varepsilon^{*}\right>\right]\left[1-T^{*\,M}\right]\,,\]

where \(\sigma_y\) is the yield stress, \(B\) is the hardening constant, \(\bar{\varepsilon}_p\) is the equivalent plastic strain, \(N\) is the hardening exponent, and \(C\) is the rate constant. The non-dimensional effective total strain rate \(\dot\varepsilon^{*}\) is given by

(5.26)\[\dot\varepsilon^{*} = \dot{\varepsilon}/\dot{\varepsilon}_{0}\,,\]

where \(\dot{\varepsilon}_{0}\) is a reference strain rate defined by the input EDOT_REF material parameter. Note if EDOT_REF is undefined, then \(\dot{\varepsilon}^{*}\) is set to the larger of either the maximum strain rate the material has encountered or the REFERENCE RATE input parameter. If EDOT_REF is defined, then the REFERENCE RATE input is not used by the model and has no effect. The Macaulay brackets in (5.25) ensure that \(\sigma\) is equal to the static flow stress \(\sigma_{\text{s}} = \left[ \sigma_y + B \left(\bar{\varepsilon}_p\right)^{N} \right]\left[ 1 - \theta^{*\,M} \right]\) when \(\dot{\varepsilon}<\dot{\varepsilon}_{0}\).

Parameter \(T^{*}\) is the homologous temperature and is defined as

(5.27)\[T^{*} = (T - T_{ref})/(T_{melt} - T_{ref})\,,\]

where \(T\) is the current temperature, \(T_{ref}\) is the reference temperature, and \(T_{melt}\) is the melt temperature. In the case where \(M \le 0\), \((1-(T^{*})^{M}) = 1\).

Note that the temperature used internal to the Johnson–Cook model is not the standard model “temperature” field. Instead, the material temperature is defined via the INITIAL TEMPERATURE command. Plastic work internal to the model results in adiabatic heating and raises the material temperature. The resulting change in temperature is computed according to

(5.28)\[\Delta T = \frac{\beta}{{\rho}C_v}\sigma_y\Delta\bar{\varepsilon}_p,\]

where \(\rho\) is the material density, \(C_v\) is the specific heat, and \(\beta\) is the fraction of plastic work that is converted to heat, where \(0 \le \beta \le 1\). By default, \(\beta = 0.95\) though it may be set to a different value with the BETA command.

The Johnson–Cook model also encapsulates a failure criterion; the damage model [[9]] has a failure strain given by

(5.29)\[\varepsilon^{f} = \left( D_{1} + D_{2}\exp\left(D_{3}\sigma^{*}\right) \right)\left( 1 + D_{4}\ln\dot{\varepsilon}^{*} \right)\left( 1+D_{5}T^{*} \right)\]

where \(D_{1}\), \(D_{2}\), \(D_{3}\), \(D_{4}\), and \(D_{5}\) are material parameters, \(\sigma^{*}\) is the triaxiality, \(\sigma^{*} = \sigma_{m}/\bar{\sigma}\), \(\dot{\varepsilon}^{*}\) is the dimensionless strain rate, and \(T^{*}\) is the homologous temperature, both defined above. Damage is accumulated over time:

(5.30)\[D = \int_{0}^{t} \frac{\dot{\bar{\varepsilon}}^{p}}{\varepsilon^{f}}dt .\]

When \(D=1\), the material has failed. By default, fracture behavior is not active. For more information about the Johnson–Cook material model, consult [[8], [9]].

5.2.17.1. Command lines

Valid command lines for a command block defining a Johnson–Cook model are as follows:

  • Elastic constants: Consult Section 5.1.5 for information on elastic constants input.

  • YIELD STRESS defines \(\sigma_{y}\), the stress for onset of yield and plasticity.

  • HARDENING CONSTANT defines \(B\).

  • HARDENING EXPONENT defines \(N\).

  • RHOCV defines \({\rho}C_v\), the volumetric heat capacity.

  • INITIAL TEMPERATURE defines the material initial temperature. Note that the Johnson–Cook material model temperature is not linked to the standard model “temperature” field that is set from BEGIN PRESCRIBED TEMPERATURE command blocks.

  • THERMAL EXPONENT defines the thermal exponent \(M\).

  • REFERENCE TEMPERATURE defines the reference temperature \(T_{ref}\).

  • MELT TEMPERATURE defines the melt temperature \(T_{melt}\).

  • REFERENCE RATE defines the reference strain rate, \(\dot{\varepsilon}_{0}\). The default value is \(0.001 \, s^{-1}\).

  • BETA defines the fraction of plastic work that is converted to heat, \(\beta\). The default is 0.95.

  • D1, D2, D3, D4, and D5 define fracture coefficients \(D_{1}\), \(D_{2}\), \(D_{3}\), \(D_{4}\), and \(D_{5}\), respectively. The default value for all coefficients is 0.0.

  • FORMULATION controls the strain rate source term. A value of 0 triggers the use of the total strain rate, while 1 uses the plastic strain rate. The plastic strain rate may be stabler since it varies monotonically and at a much lower frequency than the total strain rate.

State variables for this model are listed in Table Table 5.15.

Table 5.15 State Variables for JOHNSON COOK Model (Section 5.2.17)

Name

Variable Description

RADIUS

radius of yield surface

EQPS

equivalent plastic strain

THETA

temperature

EQDOT

effective total strain rate

ITER

EFAIL

failure strain, \(\varepsilon^{f}\)

DAMAGE

damage, \(D\)

YIELD_STRESS

yield stress

Warning

Strongly rate-dependent models may fare poorly in implicit quasistatic solution. In implicit analyses the rate term used to evaluate the current load step is the rate seen by the model in the previous load step. This may cause the solution to oscillate between high- and low-rate equilibrium states from step to step.

5.2.18. BCJ_MEM Model

BEGIN PARAMETERS FOR MODEL BCJ_MEM
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>

  YOUNGS MODULUS FUNCTION = <string> youngs_modulus_scale_factor
  POISSONS RATIO FUNCTION = <string> poissons_ratio_scale_factor
  #
  # Initial yield as function of temperature
  #
  RATE INDEPENDENT YIELD SHEAR COEFFICIENT       = <real>
  RATE INDEPENDENT YIELD CONSTANT                = <real>
  RATE INDEPENDENT YIELD TEMPERATURE DEPENDENCE  = <real>
  RATE INDEPENDENT YIELD TEMPERATURE DEPENDENCE2 = <real>
  RATE INDEPENDENT YIELD TEMPERATURE DEPENDENCE3 = <real>
  RATE INDEPENDENT YIELD TEMPERATURE DEPENDENCE4 = <real>
  #
  # Flow rule rate dependence
  #
  FLOW RULE COEFFICIENT CONSTANT               = <real>
  FLOW RULE COEFFICIENT TEMPERATURE DEPENDENCE = <real>
  FLOW RULE EXPONENT CONSTANT                  = <real>
  FLOW RULE EXPONENT TEMPERATURE DEPENDENCE    = <real>
  #
  # Isotropic hardening
  #
  ISOTROPIC HARDENING SHEAR COEFFICIENT                 = <real>
  ISOTROPIC HARDENING CONSTANT                          = <real>
  ISOTROPIC HARDENING TEMPERATURE DEPENDENCE            = <real>
  ISOTROPIC DYNAMIC RECOVERY CONSTANT                   = <real>
  ISOTROPIC DYNAMIC RECOVERY TEMPERATURE DEPENDENCE     = <real>
  ISOTROPIC STATIC RECOVERY CONSTANT                    = <real>
  ISOTROPIC STATIC RECOVERY TEMPERATURE DEPENDENCE      = <real>
  ISOTROPIC STATIC RECOVERY SINH CONSTANT               = <real>
  ISOTROPIC STATIC RECOVERY SINH TEMPERATURE DEPENDENCE = <real>
  #
  # Kinematic hardening
  #
  BACK STRESS HARDENING CONSTANT = <real>
  BACK STRESS HARDENING TEMPERATURE DEPENDENCE = <real>
  BACK STRESS DYNAMIC RECOVERY CONSTANT = <real>
  BACK STRESS DYNAMIC RECOVERY TEMPERATURE DEPENDENCE =
    <real>
  #
  # heat due to plastic dissipation
  TEMPERATURE OPTION = <real>
  PLASTIC DISSIPATION FACTOR = <real>
  DENSITY FOR PLASTIC DISSIPATION CALCULATIONS = <real>
  SPECIFIC HEAT FOR PLASTIC DISSIPATION CALCULATIONS =
    <real>
  INITIAL TEMPERATURE FOR UNCOUPLED ADIABATIC HEATING =
    <real>
  #
  # damage evolution
  DAMAGE EXPONENT                               = <real>
  VOLUMETRIC EFFECTS OF DAMAGE OPTION           = <real>
  PRESSURE INTEGRATION OPTION                   = <real>
  IMPLICIT DAMAGE SOLVER NUMBER OF ITERATIONS   = <real>
  IMPLICIT DAMAGE SOLVER RESIDUAL TOLERANCE     = <real>
  MAXIMUM CHANGE IN DAMAGE ALLOWED PER TIMESTEP = <real>
  #
  # misorientation variable
  MISORIENTATION VARIABLE HARDENING CONSTANT = <real>
  MISORIENTATION VARIABLE HARDENING EXPONENT = <real>
  #
  # integration options
  SEMI IMPLICIT PLASTIC STRAIN SOLVER NUMBER OF ITERATIONS =
    <real>
  SEMI IMPLICIT PLASTIC STRAIN SOLVER RESIDUAL TOLERANCE =
    <real>
  #
  # initial values for state variables
  #
  INITIAL KAPPA    = <real>
  INITIAL DAMAGE   = <real>
  INITIAL ZETA     = <real>
  INITIAL ALPHA_XX = <real>
  INITIAL ALPHA_XY = <real>
  INITIAL ALPHA_XZ = <real>
  INITIAL ALPHA_YY = <real>
  INITIAL ALPHA_YZ = <real>
  INITIAL ALPHA_ZZ = <real>
  #
  #  Melting related variables
  #  Optional temperature at which material turns into a fluid and
  #  basic properties of that fluid
  #
  MELT TEMPERATURE = <real>melt_temp
  FLUID VISCOSITY  = <real>fluid_viscosity
  FLUID BULK       = <real>fluid_bulk
END [PARAMETERS FOR MODEL BCJ_MEM]

The BCJ_MEM material model, like BCJ, is a rate and temperature-dependent elasto-viscoplasticity model with isotropic damage. The two models have slightly different forms for the flow rule and static recovery expressions. In addition, the BCJ_MEM model includes the effects of recrystallization and grain growth [[18]]. Currently, the temperature must be prescribed in the input deck for these models to work. This will be changed in the future.

In its full form, the BCJ_MEM model has considerable complexity, but the material parameters in the list above are all optional, with the exception of two elastic constants and a yield strength. For example, in its simplest form, BCJ_MEM can be used to model elastic, perfectly-plastic materials by specifying the following:

BEGIN PARAMETERS FOR MODEL BCJ_MEM
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  RATE INDEPENDENT YIELD CONSTANT = <real>
END [PARAMETERS FOR MODEL BCJ_MEM]

To model an elastic-plastic material with linear hardening, the line

ISOTROPIC HARDENING CONSTANT = <real>

would need to be added to specify the hardening rate. The more general form includes rate and temperature effects in the yield strength. BCJ_MEM is a state variable model that tracks history dependence through the use of internal state variables. Thus if the temperature and rate are not constant during loading, the yield stress is not a simple function of rate, temperature, and plastic strain. For the simplified case of uniaxial tension with no kinematic hardening, the following equations must be integrated to determine the current yield stress:

(5.31)\[\dot{\sigma} = E(\dot{\epsilon}-\dot{\epsilon}_p) ,\]
(5.32)\[\dot{\epsilon}_p = f({\theta})\sinh^{n({\theta})}\left<{\frac{{\sigma}}{{\kappa}+Y({\theta})}-1}\right> ,\]
(5.33)\[\dot{\kappa} = {\kappa}\frac{\dot{\mu}}{\mu} + \left[{H(\theta) - R_d(\theta)\kappa}\right]\dot\epsilon_p - R_s(\theta)\kappa\sinh\left({Q(\theta)\kappa}\right) ,\]

where \(\theta\) is the temperature and \(\kappa\) represents the isotropic hardening variable, which evolves according to a hardening minus dynamic recovery form originally proposed by Kocks and Mecking [[19]], with a static recovery term developed by Nes [[20]]. The flow rule can be inverted to obtain the yield stress:

(5.34)\[\sigma_y = \left[{Y + \kappa}\right]\left\{1+\sinh^{-1}\left[\left({\frac{\dot{\epsilon}^p}{f}}\right)^{1/n}\right]\right\} .\]

To illustrate the evolution of the yield stress for the simple case of constant strain rate, constant temperature loading with no stage IV hardening and no static recovery, the equation for the isotropic hardening variable reduces to

(5.35)\[\dot{\kappa} = \left[{H(\theta) - R_d(\theta)\kappa}\right]\dot\epsilon_p\,\]

which can be integrated analytically; the flow rule can be inverted to get the following relation for yield strength:

(5.36)\[\sigma_y = \left[{Y + \frac{H}{R_d} \left(1-e^{-R_d\epsilon_p}\right) }\right]\left\{1+\sinh^{-1}\left[\left({\frac{\dot{\epsilon}^p}{f}}\right)^{1/n}\right]\right\}\,\]

The expression in brackets represents the sum of the rate-independent yield strength and the hardening due to plastic strain; the expression in braces provides the rate dependence of the yield strength. This equation can be compared to (5.25) of the Johnson Cook model.

The temperature dependence of the initial yield strength is of the form

(5.37)\[Y(\theta) = \frac{Y_o}{Y_4+e^{-Y_1/\theta}}\left\{\frac{1}{2} \left[{1+\tanh\left({Y_2\left({Y_3-\theta}\right)}\right)}\right]\right\},\]

where \(Y_i\) are material constants.

In the event that temperature \(\theta\) is zero or unset, the functional form is modified to be

(5.38)\[Y(\theta) = \frac{Y_o}{Y_4},\]

The default value for \(Y_4=0.0\), so it is an error to leave \(Y_4\) unspecified when temperature is not provided as this results in an infinite yield surface. Furthermore, the term in braces \(\left\{\ldots\right\}\) of (5.37) is only included in the yield surface when the value for \(Y_2\neq0\). Since \(Y_2\) is zero by default, this term (and the \(1/2\) scale factor) are not included in the yield surface expression by default.

The yield can also be specified as a simple constant times the shear modulus,

(5.39)\[Y(\theta) = Y_{\mu}\mu(\theta)\]

where the shear modulus can depend on temperature through user-defined scale factors:

YOUNGS MODULUS FUNCTION = <string> youngs_modulus_scale_factor
POISSONS RATIO FUNCTION = <string> poissons_ratio_scale_factor

Similarly, the temperature dependence of the hardening parameter in the evolution equation for the isotropic hardening variable can be specified in one of two ways:

(5.40)\[H(\theta) = H_1 - H_2\theta\]

or

(5.41)\[H(\theta) = H_{\mu}\mu(\theta)\]

The other coefficients in the evolution equation for the isotropic hardening variable have an Arrhenius-type temperature dependence, as shown here for the dynamic recovery parameter:

(5.42)\[R_d(\theta) = R_{d1}e^{-R_{d2}/\theta}\]

Rate effects in the flow rule: The flow rule coefficient has an Arrhenius temperature dependence:

(5.43)\[f(\theta) = f_1e^{-f_2/\theta} .\]

The exponent in the flow rule has the following temperature dependence:

(5.44)\[n(\theta) = n_1 + \frac{n_2}{\theta} .\]

The rate dependence of the model can make the system of equations stiff. The default integration for plastic strain uses the radial return method. A semi-implicit integration scheme that is implicit in plastic strain can be selected by setting the SEMI IMPLICIT PLASTIC STRAIN SOLVER NUMBER OF ITERATIONS to whatever value is desired. If the residual does not drop below the tolerance specified by SEMI IMPLICIT PLASTIC STRAIN SOLVER RESIDUAL TOLERANCE, then the radial return value for plastic strain is used instead, and a message is sent to the output file to this effect. It is recommended to always use the semi-implicit plastic strain solver when running implicit analyses since it will improve convergence. For explicit, the errors incurred by not doing the semi-implicit integration are not significant enough to warrant the time cost of implicit iterations.

Stage IV hardening: Stage IV hardening is modeled through the misorientation variable, which loosely represents the geometrically necessary dislocation density and evolves according to the relation proposed by Kok et al. [[21]]. The misorientation variable, when used, adds an additional hardening term to the evolution equation for the isotropic hardening variable:

(5.45)\[\dot{\kappa} = {\kappa}\frac{\dot{\mu}}{\mu} + \left[{H(\theta)\left({1+\frac{\zeta}{\kappa}}\right)-R_d(\theta)\kappa}\right] \dot\epsilon_p-R_s(\theta)\kappa\sinh\left({Q(\theta)\kappa}\right)\]

The parameters in the evolution equation for the misorientation variable are independent of temperature, since they represent geometrically necessary dislocations:

(5.46)\[\frac{d}{dt}\left({\frac{\zeta}{\mu}}\right) = h_\zeta\left({\frac{\zeta}{\mu}}\right)^{1-1/r} \dot\epsilon_p\]

Heat generation due to plastic dissipation: Heat generation due to plastic dissipation can be modeled in BCJ_MEM in two ways: for coupled solid/thermal calculations (TEMPERATURE OPTION = 0), the plastic dissipation rate is stored as a state variable (AHEAT) and passed to a thermal code as a heat source term; for uncoupled calculations (TEMPERATURE OPTION = 1), temperature is stored as a state variable (THETA), and temperature evolution due to adiabatic heating is calculated within the material model. The heat generated, AHEAT, is calculated as \(\beta \sigma \dot\epsilon_p\). For uncoupled adiabatic heating, the temperature, THETA, evolves as

(5.47)\[\dot{\theta} = \frac{\beta}{\rho c_p} \sigma \dot\epsilon_p\]

where \(\beta\) is the fraction of plastic work that is dissipated as heat, \(\rho\) is the density, and \(c_p\) is the specific heat.

Isotropic damage: Isotropic damage is included in the BCJ_MEM through a void growth equation proposed by Cocks and Ashby [[22]]:

(5.48)\[\dot{\phi} = \sqrt{\frac{2}{3}}\dot\epsilon_p\frac{1-(1-\phi)^{m+1}}{(1-\phi)^m} \sinh\left[{\frac{2(2m-1)}{2m+1} \frac{<p>}{\sigma_{vm}}}\right],\]

where \(\sigma_{vm}\) is the von Mises stress, \(p\) is the hydrostatic stress, \(<\cdot>\) are Macaulay brackets, and \(m\) is the DAMAGE EXPONENT. When damage is included in the model, the yield stress decreases with damage according to

(5.49)\[\sigma_y = (1-\phi) (Y + \kappa) \left\{1+\sinh^{-1}\left[\left({\frac{\dot{\epsilon}^p}{f}}\right)^{1/n}\right]\right\}\,\]

We assume Young’s modulus and the shear modulus decrease as damage increases, according to \(E(\theta,\phi) = E(\theta) (1-\phi)\) and \(\mu(\theta,\phi) = \mu(\theta) (1-\phi)\). It then follows that the bulk modulus must vary in the same way:

(5.50)\[K(\theta,\phi) = k(\theta) (1-\phi)\]

Due to the effects of damage, the pressure evolution equation becomes:

(5.51)\[\dot p = \left[{\frac{\dot k (\theta)}{k (\theta)} - \frac{\dot\phi}{1-\phi}}\right] p + 3D_{ave}k(\theta)(1-\phi) - k(\theta)\dot\phi\]

In this equation, the last term is due to volumetric expansion of the material as voids grow. This term can lead to some non-physical responses under certain loading conditions, so its inclusion is optional in the BCJ_MEM material model and is controlled by the VOLUMETRIC EFFECTS OF DAMAGE OPTION parameter. If this optional parameter is 0 (default), then the volumetric term is not included; if the value is 1, then the volumetric term is active. The integration of the pressure equation can be selected by setting the value of PRESSURE INTEGRATION OPTION to either 0 for implicit (Backward Euler) or 1 for implicit midpoint method.

The integration algorithm for damage solves the damage equation analytically using the midpoint value for triaxiality. The default value for IMPLICIT DAMAGE SOLVER NUMBER OF ITERATIONS is 50, but can be set to whatever value is desired. If the residual does not drop below the tolerance specified by IMPLICIT DAMAGE SOLVER RESIDUAL TOLERANCE, then the value for damage from the last iteration attempt is used instead, and a message is sent to the output file to this effect.

Modeling recrystallization: Recrystallization is a process by which the microstructure in a worked material is softened by the nucleation and growth of a new set of grains with relatively low dislocation density. The method used by BCJ_MEM to model recrystallization is fully documented in Reference [[18]], so it will not be repeated here. Additional output variables when modeling recrystallization are listed in Table Table 5.17

Kinematic hardening: The yield surface in stress space can either grow (or contract) through the isotropic hardening variable or translate through evolution of the back stress, or kinematic hardening, variable. The back stress evolves according to the equation

(5.52)\[\mathring{\mathbf\alpha} = h(\theta) d^p - r_d(\theta) \dot{\epsilon}^p \sqrt{\frac{3}{2}} \|{\bf\alpha}\| \bf\alpha ,\]

where

(5.53)\[h(\theta) = h_1 - h_2\theta ,\]
(5.54)\[r_d(\theta) = r_{d1}e^{-r_{d2}/\theta} .\]

When kinematic hardening is desired, the hardening and recovery must be specified by the parameters \(h_1\), \(h_2\), \(r_{d1}\), and \(r_{d2}\).

State variable initialization: The initial values for the internal state variables are specified through the input values for \(\kappa_o\), \(\phi_o\), \(\zeta_o\), and \(\alpha_{ij_o}\). The default values for the initial values of \(\kappa_o\), \(\zeta_o\) and \(X_o\) are 1.0e-6 to avoid singularities in the evolution equations.

Output variables available for this model are listed in Tables Table 5.16 and Table 5.17.

Table 5.16 State Variables for BCJ_MEM Model

Name

Variable Description

BACK_STRESS_XX

back stress tensor - xx component

BACK_STRESS_YY

back stress tensor - yy component

BACK_STRESS_ZZ

back stress tensor - zz component

BACK_STRESS_XY

back stress tensor - xy component

BACK_STRESS_YZ

back stress tensor - yz component

BACK_STRESS_ZX

back stress tensor - zx component

KAPPA

hardening scalar

DAMAGE

void volume fraction

DAMAGE_RATE

rate of change of void volume fraction

EQPS

equivalent plastic strain

THETA

temperature for adiabatic heating

AHEAT

plastic dissipation rate

EQPSDOT

plastic strain rate

SIGY_RT

room temperature yield stress at quasistatic conditions

IBOND

contact variable to switch from sliding to glued contact based on recrystallized volume fraction
Table 5.17 Additional state Variables for BCJ_MEM Model When Modeling Recrystallization

Name

Variable Description

GRAIN_SIZE

grain size

REX_CYCLE_A

recrystallized volume fraction for cycle A

REX_CYCLE_B

recrystallized volume fraction for cycle B

REX_CYCLE_C

recrystallized volume fraction for cycle C

REX_CYCLE_D

recrystallized volume fraction for cycle D

BACK_STRESS_NO_REX_XX

xx component of back stress in un-recrystallized volume fraction

BACK_STRESS_NO_REX_YY

yy component of back stress in un-recrystallized volume fraction

BACK_STRESS_NO_REX_ZZ

zz component of back stress in un-recrystallized volume fraction

BACK_STRESS_NO_REX_XY

xy component of back stress in un-recrystallized volume fraction

BACK_STRESS_NO_REX_YZ

yz component of back stress in un-recrystallized volume fraction

BACK_STRESS_NO_REX_ZX

zx component of back stress in un-recrystallized volume fraction

SKAPP_NO_REX

isotropic hardening in the un-recrystallized volume fraction

SKAPP_CYCLE_A

isotropic hardening in the recrystallized volume fraction for cycle A

SKAPP_CYCLE_B

isotropic hardening in the recrystallized volume fraction for cycle B

SKAPP_CYCLE_C

isotropic hardening in the recrystallized volume fraction for cycle C

SKAPP_CYCLE_D

isotropic hardening in the recrystallized volume fraction for cycle D

ZETA_NO_REX

misorientation in the un-recrystallized volume fraction

ZETA_CYCLE_A

misorientation in the un-recrystallized volume fraction for cycle A

ZETA_CYCLE_B

misorientation in the un-recrystallized volume fraction for cycle B

ZETA_CYCLE_C

misorientation in the un-recrystallized volume fraction for cycle C

ZETA_CYCLE_D

misorientation in the un-recrystallized volume fraction for cycle D

Further questions about the model, or requests for changes/enhancements, can be sent to aabrown@sandia.gov.

Warning

Strongly rate-dependent models may fare poorly in implicit quasistatic solution. In implicit analyses the rate term used to evaluate the current load step is the rate seen by the model in the previous load step. This may cause the solution to oscillate between high- and low-rate equilibrium states from step to step.

5.2.19. Power Law Creep Model

BEGIN PARAMETERS FOR MODEL POWER_LAW_CREEP
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Viscoplastic parameters
  #
  CREEP CONSTANT    = <real>
  CREEP EXPONENT    = <real>
  THERMAL CONSTANT  = <real>
  MAX SUBINCREMENTS = <integer> max_subincrements(100)
END [PARAMETERS FOR MODEL POWER_LAW_CREEP]

The power law creep model describes the secondary (or steady-state) creep and is useful in capturing the time-dependent behavior of metals, brazes, or solder at high homologous temperatures. It may also be used as a simple model for the time-dependent behavior of geologic materials such as salt. A general discussion of such creep behaviors and the associated modeling may be found in the texts of [[23], [24]] while the specific implementation used here is discussed in [[4]].

In the power law creep model, the effective creep strain rate is taken to be explicitly a function of stress and temperature. A power law relation is used for the stress dependence while an Arrhenius like expression is used to capture thermal effects. As such, the effective creep strain rate is written as,

(5.55)\[ \dot{\bar{\varepsilon}}^{\text{c}} = A\bar{\sigma}_{vM}^{m} \exp{\left(\frac{-Q}{R\theta}\right)}\,,\]

where \(\dot{\bar{\varepsilon}}^{\text{c}}\) is the effective creep strain rate, \(\bar{\sigma}_{vM}\) is the von Mises stress, \(A\) is the creep constant, \(m\) is the creep exponent, \(Q\) is the activation energy, \(R\) is the universal gas constant (1.987 cal/mole K), and \(\theta\) is the absolute temperature. As a slip based mechanism, it is assumed that the creep strains are deviatoric leading to a 3D evolution law of the form,

\[D^{\text{c}}_{ij}=\dot{\bar{\varepsilon}}^{\text{c}}\frac{3}{2}\frac{s_{ij}}{\bar{\sigma}_{vM}},\]

with \(s_{ij}\) being the deviatoric stress. The corresponding incremental constitutive equation for this model is then given as,

(5.56)\[\stackrel{\circ}{\sigma}_{ij}=\mathbb{C}_{ijkl}\left(D_{kl}-D^{\text{c}}_{kl}\right).\]

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input.

  • The creep constant, \(A\), in Equation (5.55) is defined with the CREEP CONSTANT command line.

  • The creep exponent, \(m\), in Equation (5.55) is defined with the CREEP EXPONENT command line.

  • The thermal constant, \(Q/R\) in Equation (5.55) is defined with the THERMAL CONSTANT command line.

  • time step sub incrementation within the material model may be used to accurately calculate the true creep stress. The maximum sub-increments in a load step is defined with the MAX SUBINCREMENTS command line. The default is 100. A larger number of steps can potentially improve accuracy if a large amount of creep happens in a single step. A smaller number of steps can sometimes improve analysis speed.

Output variables available for this model are listed in Table 5.18.

Table 5.18 State Variables for POWER LAW CREEP Model (Section 5.2.19)

Name

Description

ECREEP

equivalent creep strain

SEQDOT

equivalent stress rate

5.2.20. Viscoplastic Model

BEGIN PARAMETERS FOR MODEL VISCOPLASTIC
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>

  FLOW RATE     = <real>
  SINH EXPONENT = <real>
  ALPHA         = <real>
  ISO HARDENING = <real>
  ISO RECOVERY  = <real>
  ISO EXPONENT  = <real>
  KIN HARDENING = <real>
  KIN RECOVERY  = <real>
  KIN EXPONENT  = <real>
  FLOW STRESS   = <real>

  SHEAR FUNCTION    = <string>
  BULK FUNCTION     = <string>
  RATE FUNCTION     = <string>
  EXPONENT FUNCTION = <string>
  ALPHA FUNCTION    = <string>
  IHARD FUNCTION    = <string>
  IREC FUNCTION     = <string>
  KHARD FUNCTION    = <string>
  KREC FUNCTION     = <string>
  MAX SUBINCREMENTS = <int> itmax (2000)
END [PARAMETERS FOR MODEL VISCOPLASTIC]

The viscoplastic model is a rate dependent plasticity model that is useful for modeling solders and brazes and was developed by Neilsen et al. [[25]]. This model is formulated in terms of the stress rate for the material. Like many inelastic models, the rate of deformation, \(D_{ij}\), is additively decomposed into an elastic, \(D_{ij}^{\text{e}}\), and an inelastic, \(D_{ij}^{\text{in}}\) part such that,

\[D_{ij} = D_{ij}^{\text{e}} + D_{ij}^{\text{in}}.\]

The elastic rate of deformation is the only part that contributes to the stress rate and it does so through the elastic moduli, \(\mathbb{C}_{ijkl}\), in a linear fashion leading to the relation,

(5.57)\[\stackrel{\circ}{\sigma}_{ij} = \mathbb{C}_{ijkl} D_{kl}^{\text{e}},\]

where \(\mathbb{C}_{ijkl}\) are the components of the fourth-order, isotropic elasticity tensor. The stress rate is arbitrary, as long as it is objective. Two objective stress rates are commonly used: the Jaumann rate and the Green-McInnis rate. For problems with fixed principal axes of deformation, these two rates give the same answers. For problems where the principal axes of deformation rotate during the deformation, the two rates can give different answers. Generally speaking there is no reason to pick one objective rate over another.

The inelastic strain rate is a function of the stress state, \(\sigma_{ij}\), the temperature, \(\theta\), and a number of internal state variables including both scalar isotropic, \(D\), and tensorial kinematic, \(B_{ij}\), hardening variables. With these dependencies defined, a general form for the evolution of the inelastic deformation may be given by,

\[D_{ij}^{\text{in}} = \frac{3}{2} \gamma\left( \sigma_{ij}, \theta; D, B_{ij} \right) n_{ij},\]

where \(n_{ij}\) is the direction of inelastic deformation and is defined as,

(5.58)\[n_{ij}=\frac{1}{\tau}\left(s_{ij}-\frac{2}{3}B_{ij}\right),\]

and

\[\tau=\sqrt{\frac{3}{2}\left(s_{ij}-\frac{2}{3}B_{ij}\right)\left(s_{ij}-\frac{2}{3}B_{ij}\right)},\]

with \(s_{ij}\) being the deviatoric stress tensor. The inelastic strain rate, \(\gamma\), is defined via a hyperbolic sin law,

(5.59)\[\gamma = f(\theta)\left[ \sinh\left( \frac{\tau}{\alpha(\theta) D} \right) \right]^{p(\theta)},\]

where \(f(\theta) = \exp(g(\theta))\). The expressions \(g(\theta)\), \(\alpha(\theta)\), and \(p(\theta)\) are model parameters that are functions of temperature.

The evolution laws for the state variables \(D\) and \(B_{ij}\) are,

(5.60)\[\dot{D} = \frac{A_{1}}{\left( D-D_{0} \right)^{A_{3}}}\gamma - A_{2}\left( D-D_{0} \right)^{2},\]

and

(5.61)\[\dot{B}_{ij} = \frac{A_{4}}{b^{A_{6}}} D_{ij}^{\text{in}} - A_{5} b B_{ij},\]

where

\[b = \sqrt{\frac{2}{3}B_{ij}B_{ij}}.\]

The parameters \(D_{0}\), \(A_{1}\), \(A_{2}\), \(A_{3}\), \(A_{4}\), \(A_{5}\) and \(A_{6}\) are model parameters. The parameters \(A_{1}\), \(A_{2}\), \(A_{4}\) and \(A_{5}\) are also functions of temperature. The model can be simplified with the appropriate choice of these parameters.

The following material parameters are functions of temperature and have the following form

\[\begin{split}G(\theta) = G_{0} h_{G}(\theta) \;\;\; ; \;\;\; K(\theta) = K_{0} h_{K}(\theta) \nonumber \\ \nonumber \\ g(\theta) = g_{0} h_{g}(\theta) \;\;\; ; \;\;\; p(\theta) = p_{0} h_{p}(\theta) \;\;\; ; \;\;\; \alpha (\theta) = \alpha_{0} h_{\alpha}(\theta) \nonumber \\ \\ A_{1} (\theta) = A_{1}^{0} h_{1}(\theta) \;\;\; ; \;\;\; A_{2} (\theta) = A_{2}^{0} h_{2}(\theta) \nonumber \\ \nonumber \\ A_{4} (\theta) = A_{4}^{0} h_{4}(\theta) \;\;\; ; \;\;\; A_{5} (\theta) = A_{5}^{0} h_{5}(\theta) \nonumber\end{split}\]

where the functions \(h_{*}(\theta)\) are normalized functions of temperature and the values \((*)_{0}\) or \((*)^{0}\) are the reference values that are input in the command block.

In the above command blocks:

  • Since the model requires functions to describe the temperature dependence of the bulk and shear modulus, it is recommended that one inputs the bulk and shear modulus at some reference temperature. However, any two of the elastic constants can be used for input. See Section 5.1.5 for more information on elastic constants input.

  • The reference value in the equation for the flow rate, \(\ln f_{0}\), is defined with the FLOW RATE command line.

  • The reference value for the exponent on the \(\sinh\) function, \(p_{0}\), is defined with the SINH EXPONENT command line.

  • The reference value \(alpha_{0}\) is defined with the ALPHA command line.

  • The reference value for the isotropic hardening parameter, \(A_{1}^{0}\), is defined with the ISO HARDENING command line.

  • The reference value for the isotropic recovery parameter, \(A_{2}^{0}\), is defined with the ISO RECOVERY command line.

  • The value for the isotropic hardening exponent parameter, \(A_{3}\), is defined with the ISO EXPONENT command line.

  • The reference value for the kinematic hardening parameter, \(A_{4}^{0}\), is defined with the KIN HARDENING command line.

  • The reference value for the kinematic recovery parameter, \(A_{5}^{0}\), is defined with the KIN RECOVERY command line.

  • The value for the kinematic hardening exponent parameter, \(A_{6}\), is defined with the KIN EXPONENT command line.

  • The value for the flow stress, \(D_{0}\), is defined with the FLOW STRESS command line.

  • The user-defined and normalized function that gives the shear modulus as a function of temperature, \(h_{G}(\theta)\), is defined with the SHEAR FUNCTION command line.

  • The user-defined and normalized function that gives the bulk modulus as a function of temperature, \(h_{K}(\theta)\), is defined with the BULK FUNCTION command line.

  • The user-defined and normalized function that gives the flow rate as a function of temperature, \(h_{g}(\theta)\), is defined with the RATE FUNCTION command line.

  • The user-defined and normalized function that gives the \(\sinh\) exponent as a function of temperature, \(h_{p}(\theta)\), is defined with the EXPONENT FUNCTION command line.

  • The user-defined and normalized function that gives \(\alpha\) as a function of temperature, \(h_{\alpha}(\theta)\), is defined with the ALPHA FUNCTION command line.

  • The user-defined and normalized function that gives \(A_{1}\) as a function of temperature, \(h_{1}(\theta)\), is defined with the IHARD FUNCTION command line.

  • The user-defined and normalized function that gives \(A_{2}\) as a function of temperature, \(h_{2}(\theta)\), is defined with the IREC FUNCTION command line.

  • The user-defined and normalized function that gives \(A_{4}\) as a function of temperature, \(h_{4}(\theta)\), is defined with the KHARD FUNCTION command line.

  • The user-defined and normalized function that gives \(A_{5}\) as a function of temperature, \(h_{5}(\theta)\), is defined with the KREC FUNCTION command line.

  • The Viscoplastic model may need to take sub-increments to solve for the plastic flow over the current time step. The maximum number of steps that may be taken on a step prior to issuing an error can be set by the MAX SUBINCREMENTS command line. This value defaults to 2000.

Output variables available for this model are listed in Table 5.19.

More information on the model can be found in the report by Neilsen, et. al. [[25]].

Table 5.19 State Variables for VISCOPLASTIC Model (Section 5.2.20)

Name

Description

EQPS

equivalent plastic strain

SVB

kinematic hardening variable, \({\bf B}\)

SVB_XX

kinematic hardening variable - xx component, \(B_{xx}\)

SVB_YY

kinematic hardening variable - yy component, \(B_{yy}\)

SVB_ZZ

kinematic hardening variable - zz component, \(B_{zz}\)

SVB_XY

kinematic hardening variable - xy component, \(B_{xy}\)

SVB_YZ

kinematic hardening variable - yz component, \(B_{yz}\)

SVB_ZX

kinematic hardening variable - zx component, \(B_{zx}\)

SVD

isotropic hardening variable, \(D\)

EQDOT

inelastic strain rate, \(\gamma\)

COUNT

number of sub-increments

SHEAR

shear modulus, \(G(\theta)\)

BULK

bulk modulus, \(K(\theta)\)

RATE

\(g(\theta)\) (see:eq:materials-eq-vpedot)

EXP

\(p(\theta)\) (see:eq:materials-eq-vpedot)

ALPHA

\(\alpha(\theta)\) (see:eq:materials-eq-vpedot)

A1

isotropic hardening parameter, \(A_{1}(\theta)\)

A2

isotropic recovery parameter, \(A_{2}(\theta)\)

A4

kinematic hardening parameter, \(A_{4}(\theta)\)

A5

kinematic recovery parameter, \(A_{5}(\theta)\)

5.2.21. Munson-Dawson Viscoplastic Model

BEGIN PARAMETERS FOR MODEL MD_VISCOPLASTIC
  # Elastic constants
  YOUNGS MODULUS  = <real>
  POISSONS RATIO  = <real>
  SHEAR MODULUS   = <real>
  BULK MODULUS    = <real>
  LAMBDA          = <real>
  TWO MU          = <real>
  # Steady-state creep parameters
  A0              = <real> (0.0)
  A1              = <real> (0.0)
  A2              = <real> (0.0)
  Q0oR            = <real> (0.0)
  Q1oR            = <real> (0.0)
  Q2oR            = <real> (0.0)
  n0              = <real> (0.0)
  n1              = <real> (0.0)
  n2              = <real> (0.0)
  sigma_g         = <real>
  B0              = <real> (0.0)
  B1              = <real> (0.0)
  B2              = <real> (0.0)
  q               = <real> (0.0)
  # Transient creep parameters
  K0              = <real> (0.0)
  K1              = <real> (0.0)
  c0              = <real> (0.0)
  c1              = <real> (0.0)
  m0              = <real> (0.0)
  m1              = <real> (0.0)
  alpha_h         = <real> (0.0)
  alpha_r         = <real> (0.0)
  beta_h          = <real> (0.0)
  beta_r          = <real> (0.0)
  # Other parameters
  alpha           = <real> (0.0)
  a               = <real> (1000.0)
  # Numerical implementation parameters (see LAME manual)
  _chi            = <real> (2.0)
  _sigma_min      = <real> (mu*1e-10)
  _sqrt_omega_max = <real> (1e-11)
  _xi             = <real> (1e-4)
  _gamma          = <real> (0.1)
  _k_max          = <real> (100)
  _j_max          = <real> (10)
END [PARAMETERS FOR MODEL MD_VISCOPLASTIC]

The Munson-Dawson (MD) model was originally defined in [[26], [27], [28]], but several changes were made in [[29]]. This section presents the current version of the model. Note that compressive stresses and strains are treated as positive in this section, as is common in the geomechanics literature.

The MD model is an isotropic, hypoelastic, unified viscoplastic, material model. The total strain rate \(\dot{\varepsilon}_{ij}\) is decomposed into an elastic strain rate \(\dot{\varepsilon}^{\text{el}}_{ij}\), a thermal strain rate \(\dot{\varepsilon}^{\text{th}}_{ij}\), and a viscoplastic strain rate \(\dot{\varepsilon}^{\text{vp}}_{ij}\):

(5.62)\[\dot{\varepsilon}_{ij} = \dot{\varepsilon}^{\text{el}}_{ij} + \dot{\varepsilon}^{\text{th}}_{ij} + \dot{\varepsilon}^{\text{vp}}_{ij}.\]

The elastic portion of the MD model utilizes the following simple linear relationship between \(\dot{\varepsilon}^{\text{el}}_{kl}\) and the stress rate \(\dot{\sigma}_{ij}\),

\[\begin{split}\dot{\sigma}_{ij} &= \mathbb{C}_{ijkl}\dot{\varepsilon}^{\text{el}}_{kl} = \mathbb{C}_{ijkl}\left(\dot{\varepsilon}_{kl} - \dot{\varepsilon}^{\text{th}}_{kl} - \dot{\varepsilon}^{\text{vp}}_{kl}\right) \\ \mathbb{C}_{ijkl} &= (B-2/3\,\mu)\,\delta_{ij}\,\delta_{kl} + \mu\,\left(\delta_{ik}\,\delta_{jl} + \delta_{il}\,\delta_{jk}\right) ,\end{split}\]

where \(\mathbb{C}_{ijkl}\) is the elastic stiffness, which is composed of the bulk modulus \(B\), the shear modulus \(\mu\), and the Kronecker Delta \(\delta_{ij}\). The thermal strain portion of the model is simply

(5.63)\[\dot{\varepsilon}^{\text{th}}_{ij} = -\alpha\,\dot{\theta}\,\delta_{ij}\]

where \(\alpha\) is the coefficient of thermal expansion, and \(\theta\) is the temperature. Sierra/SM also offers thermal strain functions for adding thermal strain effects to any given model. If \(\alpha\ne0\), then MD model users should not specify a thermal strain function, otherwise thermal strains will be applied twice.

Plastic deformation is assumed to be isochoric and only occurs in the presence of shear stress. The MD model utilizes the Hosford stress as its equivalent shear stress measure \(\bar{\sigma}\). The Hosford stress is

(5.64)\[\bar{\sigma} = \left\{\frac{1}{2}\left[|\sigma_1 - \sigma_2|^a + |\sigma_2 - \sigma_3|^a + |\sigma_1 - \sigma_3|^a\right]\right\}^{1/a},\]

where \(\sigma_i\) are the principal stresses and \(a\) is a material parameter. This definition for \(\bar{\sigma}\) was proposed in [[13]] because it encompasses the Tresca stress (\(a=1\)), the von Mises stress (\(a=2\)), and a range of behaviors in-between (\(1<a<2\)). One can also reproduce the Tresca stress with \(a=\infty\), the von Mises stress with \(a=4\), and behaviors in-between with \(4<a<\infty\). This second range avoids potential singularities in the first and second derivatives of (5.64), so the exponent is restricted to \(a\ge4\).

The viscoplastic strain evolves according to an associated flow rule

(5.65)\[\dot{\varepsilon}^{\text{vp}}_{ij} = \dot{\bar{\varepsilon}}^{\text{vp}}\frac{\partial\bar{\sigma}}{\partial\sigma_{ij}},\]

where \(\dot{\bar{\varepsilon}}^{\text{vp}}\) is the equivalent viscoplastic strain rate. It can be decomposed into two components

\[\dot{\bar{\varepsilon}}^{\text{vp}} = \dot{\bar{\varepsilon}}^{\text{tr}} + \dot{\bar{\varepsilon}}^{\text{ss}},\]

where \(\dot{\bar{\varepsilon}}^{\text{tr}}\) is the transient equivalent viscoplastic strain rate and \(\dot{\bar{\varepsilon}}^{\text{ss}}\) is the steady state equivalent viscoplastic strain rate.

The MD model decomposes the steady state behavior into four “mechanisms”:

(5.66)\[\begin{split}\dot{\bar{\varepsilon}}^{\text{ss}} =& \sum^3_{i=0} \dot{\bar{\varepsilon}}^{\text{ss}}_i \notag \\ \dot{\bar{\varepsilon}}^{\text{ss}}_i =& A_i\,\exp\left(-\frac{Q_i}{R\,\theta}\right)\,\left(\frac{\bar{\sigma}}{\mu}\right)^{n_i} \quad \text{for } i = 0, 1, \text{ and } 2\notag \\ \dot{\bar{\varepsilon}}^{\text{ss}}_3 =& H(\bar{\sigma}-\bar{\sigma}_{\text{g}})\sum^2_{i=0}B_i\,\exp\left(-\frac{Q_i}{R\,\theta}\right)\,\mathrm{sinh}\left(q\frac{(\bar{\sigma}-\bar{\sigma}_{\text{g}})}{\mu} \right),\end{split}\]

The variables \(A_i\), \(B_i\), \(Q_i\), \(n_i\), \(\bar{\sigma}_{\text{g}}\), and \(q\) are all model parameters. All four mechanisms have an Arrhenius temperature dependence, where \(Q_i\) is an activation energy and \(R=8.314\) J/(K mol) is the universal gas constant. Mechanism 3 is only activated when \(\bar{\sigma}\) exceeds \(\bar{\sigma}_{\text{g}}\), as reflected in the heaviside function \(H(\bar{\sigma}-\bar{\sigma}_{\text{g}})\). Typically, the parameters \(B_i\) are chosen to produce a smooth transition to mechanism 3 at \(\bar{\sigma}_{\text{g}}\).

The simple functional forms of (5.66) suffice for the steady-state behavior, but the transient behavior is somewhat more complex. During work hardening under constant stress, \(\bar{\varepsilon}^{\text{tr}}\) approaches the transient strain limit \(\bar{\varepsilon}^{\text{tr*}}\) from below, and the total viscoplastic strain rate slows down over time. During recovery under constant stress, \(\bar{\varepsilon}^{\text{tr}}\) approaches \(\bar{\varepsilon}^{\text{tr*}}\) from above, and the total viscoplastic strain rate speeds up over time. The rate that \(\bar{\varepsilon}^{\text{tr}}\) approaches \(\bar{\varepsilon}^{\text{tr*}}\) is governed by

(5.67)\[\dot{\bar{\varepsilon}}^{\text{tr}} = \left(F-1\right)\,\dot{\bar{\varepsilon}}^{\text{ss}},\]

where

(5.68)\[F = \exp\left[\text{sign\,}(\bar{\varepsilon}^{\text{tr*}} - \bar{\varepsilon}^{\text{tr}})\,\kappa\,\left(1-\displaystyle{\frac{\bar{\varepsilon}^{\text{tr}}}{\bar{\varepsilon}^{\text{tr*}}}}\right)^2\right].\]

and \(\kappa\) is a quantity that depends on whether the material is work hardening or recovering. These two behaviors are captured in the following equations

(5.69)\[\begin{split}\kappa = \begin{cases} \alpha_{\mathrm{h}} + \beta_{\text{h}}\,\log_{10}\left(\displaystyle{\frac{\bar{\sigma}}{\mu}}\right) & \bar{\varepsilon}^{\text{tr}} \leq \bar{\varepsilon}^{\text{tr*}} \\ \alpha_{\mathrm{r}} + \beta_{\text{r}}\,\log_{10}\left(\displaystyle{\frac{\bar{\sigma}}{\mu}}\right) & \bar{\varepsilon}^{\text{tr}} > \bar{\varepsilon}^{\text{tr*}}. \end{cases}\end{split}\]

where \(\alpha_j\) and \(\beta_j\) are model parameters. Note that the parameter \(\kappa\) must be non-negative, otherwise (5.67) produces a negative/positive \(\dot{\bar{\varepsilon}}^{\text{tr}}\) when \(\bar{\varepsilon}^{\text{tr}}\) is below/above \(\bar{\varepsilon}^{\text{tr*}}\). (Such behavior occurs during reverse creep, but the MD model is only designed to model forward creep.) To enforce this, (5.69) is calculated first, and then

\[\kappa \leftarrow \max(\kappa, 0)\]

is applied.

The MD model uses two mechanisms to endow \(\bar{\varepsilon}^{\text{tr*}}\) with stress and temperature dependence:

\[\begin{split}\bar{\varepsilon}^{\text{tr*}} &= \sum^1_{i=0} \bar{\varepsilon}^{\text{tr*}}_i \\ \bar{\varepsilon}^{\text{tr*}}_i &= K_i\,\exp(c_i\,\theta)\left(\frac{\bar{\sigma}}{\mu}\right)^{m_i},\end{split}\]

where \(K_i\), \(c_i\), and \(m_i\) are parameters to be calibrated against experimental results.

In the command blocks that define the MD viscoplastic model:

  • See Section 5.1.5 for more information on elastic constants input.

Output variables available for this model are listed in Table 5.20.

Table 5.20 State Variables for MD_VISCOPLASTIC Model (Section 5.2.21)

Name

Description

EQ_TR_STRAIN

equivalent transient viscoplastic strain, \(\bar{\varepsilon}^{\text{tr}}\)

EQ_VP_STRAIN

equivalent viscoplastic strain, \(\bar{\varepsilon}^{\text{vp}}\)

EQ_STRESS

equivalent stress, \(\bar{\sigma}\)

VP_RATE_SCALE_FACTOR

viscoplastic rate scale factor, \(s\)

5.2.22. Soil and Crushable Foam Model

BEGIN PARAMETERS FOR MODEL SOIL_FOAM
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Yield surface parameters
  #
  A0 = <real>
  A1 = <real>
  A2 = <real>
  PRESSURE CUTOFF   = <real>
  PRESSURE FUNCTION = <string>
END [PARAMETERS FOR MODEL SOIL_FOAM]

The soil and crushable foam model is a plasticity model that can be used for modeling soil, crushable foam, or other highly compressible materials. Given the right input, the model is a Drucker-Prager model.

For the soil and crushable foam model, the yield surface is a surface of revolution about the hydrostat in principal stress space. A planar end cap is assumed for the yield surface so that the yield surface is closed. The yield stress \(\sigma_{yd}\) is specified as a polynomial in pressure \(p\). The yield stress is given as:

(5.70)\[\sigma _{yd} = a_0 + a_1 p + a_2p^{2}\,,\]

where the pressure \(p\) is positive in compression. The determination of the yield stress from Equation (5.70) places severe restrictions on the admissible values of \(a_{0}\), \(a_{1}\), and \(a_{2}\). There are three valid cases for the yield surface. In the first case, there is an elastic–perfectly plastic deviatoric response, and the yield surface is a cylinder oriented along the hydrostat in principal stress space. In this case, \(a_{0}\) is positive, and \(a_{1}\) and \(a_{2}\) are zero. In the second case, the yield surface is conical. A conical yield surface is obtained by setting \(a_{2}\) to zero and using appropriate values for \(a_{0}\) and \(a_{1}\). In the third case, the yield surface has a parabolic shape. For the parabolic yield surface, all three coefficients in Equation (5.70) are nonzero. The coefficients are checked to determine that a valid negative tensile-failure pressure can be derived based on the specified coefficients.

For the case of the cylindrical yield surface (e.g., \(a_0 > 0\) and \(a_{1} = a_{2} = 0\)), there is no tensile-failure pressure. For the other two cases, the computed tensile-failure pressure may be too low. To handle the situations where there is no tensile-failure pressure or the tensile-failure pressure is too low, a pressure cutoff can be defined. If a pressure cutoff is defined, the tensile-failure pressure is the larger of the computed tensile-failure pressure and the defined cutoff pressure.

The plasticity theories for the volumetric and deviatoric parts of the material response are completely uncoupled. The volumetric response is computed first. The mean pressure \(p\) is assumed to be positive in compression, and a yield function \(\phi_{p}\) is written for the volumetric response as:

(5.71)\[\phi_p = p - f_p \left( {\varepsilon _{V} } \right)\,,\]

where \(f_p \left( {\varepsilon _{V} } \right)\) defines the volumetric stress-strain curve for the pressure. The yield function \(\phi_{p}\) determines the motion of the end cap along the hydrostat.

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input.

  • The constant coefficient in the equation for the yield surface ( (5.70)) is defined with the A0 command line.

  • The coefficient for the linear term in the equation for the yield surface ( (5.70)) is defined with the A1 command line.

  • The coefficient for the quadratic term in the equation for the yield surface ( (5.70)) is defined with the A2 command line.

  • The user-defined maximum tensile-failure pressure is defined with the PRESSURE CUTOFF command line.

  • The pressure as a function of volumetric strain is defined with the function named on the PRESSURE FUNCTION command line.

For information about the soil and crushable foam model, see the PRONTO3D document listed as Reference [[30]]. The soil and crushable foam model is the same as the soil and crushable foam model in PRONTO3D. The PRONTO3D model is based on a material model developed by Krieg [[31]]. The Krieg version of the soil and crushable foam model was later modified by Swenson and Taylor [[32]]. The soil and crushable foam model developed by Swenson and Taylor is the model in PRONTO3D and is also the shared model for Presto and Adagio.

Output variables available for this model are listed in Table 5.21.

Table 5.21 State Variables for SOIL FOAM Model (Section 5.2.22)

Name

Description

EVOL_MAX

maximum volumetric strain seen by the material point

EVOL_FRAC

volumetric strain for tensile fracture

EVOL

current volumetric strain

EQPS

equivalent plastic strain

5.2.23. Foam Plasticity Model

BEGIN PARAMETERS FOR MODEL FOAM_PLASTICITY
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  #
  #
  PHI             = <real>
  SHEAR STRENGTH  = <real>
  SHEAR HARDENING = <real>
  SHEAR EXPONENT  = <real>
  HYDRO STRENGTH  = <real>
  HYDRO HARDENING = <real>
  HYDRO EXPONENT  = <real>
  BETA            = <real>
  P0              = <real>
END [PARAMETERS FOR MODEL FOAM_PLASTICITY]

The foam plasticity model was developed to describe the response of porous materials (like closed-cell polyurethane foams) exhibiting irreversible, elastic-plastic like responses through large deformations. Such foams can exhibit significant plastic deviatoric and volumetric strains leading to permanent shape and volume changes, respectively. The former behavior is quite typical of metals and corresponding theories are well established. The latter response, however, is not typical of metals and a theory combining these two behaviors is needed. Given these responses of interest, the foam plasticity model is well suited to use with metal foams and many closed-cell polymeric foams (e.g. polyurethane, polystyrene bead, etc.) subjected to large deformations. As permanent strains are of interest, this model is not appropriate for use with flexible foams that return to their undeformed shape after loads are removed.

Specifically, the model developed by Neilsen et al. [[33]] seeks to capture the response associated with three distinct deformation regimes. First, when foams are initially compressed, they typically exhibit an elastic response. After sufficient load is applied, a plateau of nearly constant stress over a large deformation region is noted as pores start to compress and cell walls undergo substantial deformation. Eventually, the various collapsed cells and walls begin to interact and a densification response with substantial hardening is observed. Details of these deformation processes may be found in the text of Gibson and Ashby [[34]].

Like other plasticity-based models, the incremental constitutive law for the foam plasticity model is written as,

\[\stackrel{\circ}{\sigma}_{ij}=\mathbb{C}_{ijkl}D^{\text{e}}_{kl},\]

where an additive decomposition of the strain rates such that \(D_{ij}=D^{\text{e}}_{ij}+D^{\text{p}}_{ij}\) is assumed. To describe the inelastic response of the foams of interest, Neilsen and coworkers [[33]] proposed a yield function of the form

(5.72)\[f=\frac{\bar{\sigma}^2}{a^2}+\frac{p^2}{b^2}-1,\]

where \(\bar{\sigma}\) is the von Mises effective stress (\(\bar{\sigma}=\sqrt{\left(3/2\right)s_{ij}s_{ij}}\) with \(s_{ij}\) being the deviatoric stress) and \(p\) being the hydrostatic pressure (\(p=\left(1/3\right)\sigma_{kk}\)). In such a form, the initial yield surface forms an ellipsoid about the hydrostat. The two denominators, \(a\) and \(b\), are state variables capturing hardening effects and have the functional form of,

\[\begin{split}a & = A_0+A_1\phi^{A_2}, \\ b & = \begin{cases} B_0 + B_1\phi^{B_2}, & \text{if } p \geq 0 \\ B_0, & \text{if } p < 0 \end{cases}\end{split}\]

with \(A_0, A_1, A_2, B_0, B_1,\) and \(B_2\) being model parameters and \(\phi\) being the maximum volume fraction of solid material obtained through the loading history and is defined as,

\[\phi = \max\left(\phi_c\right)\]

where,

\[\phi_c=\phi_0\frac{V_0}{V},\]

in which \(\phi_0\) is the initial volume fraction of solid material and \(V_0\) and \(V\) are the initial volume and current volume, respectively, of the foam. Put in terms of the deformation,

\[\phi_c = \phi_0\frac{1}{1+\varepsilon_{\text{V}}},\]

where \(\varepsilon_{\text{V}}\) is the engineering volume strain.

To describe the inelastic plastic deformation, a non-associated flow rule is used. Specifically,

\[D^{\text{p}}_{ij}=\dot{\gamma}g_{ij},\]

where \(\dot{\gamma}\) is the consistency multiplier found by enforcing the corresponding condition and

(5.73)\[g_{ij}=\frac{\left(1-\beta\right)g^{\text{a}}_{ij}+\beta g^{\text{r}}_{ij}}{|\left(1-\beta\right)g^{\text{a}}_{ij}+\beta g^{\text{r}}_{ij}|},\]

with the superscripts “a” and “r” being used to denote associated and radial flow directions, respectively. The model parameter \(\beta\) is introduced in (5.73) to enable associated (\(\beta=0\)), radial (\(\beta=1\)), or a linear combination of the two flow rules (\(0<\beta<1\)) to be used. The two direction vectors may written as,

\[\begin{split}g^{\text{a}}_{ij} & = \frac{\frac{\partial f}{\partial \sigma_{ij}}}{|\frac{\partial f}{\partial\sigma_{kl}}|} = \frac{\frac{3}{a^2}s_{ij}+\frac{2}{3b^2}p\delta_{ij}}{|\frac{3}{a^2}s_{ij}+\frac{2}{3b^2}p\delta_{ij}|}, \\ g^{\text{r}}_{ij} & = \frac{\sigma_{ij}}{|\sigma_{kl}|}=\frac{\sigma_{ij}}{\sqrt{\sigma_{kl}\sigma_{kl}}}.\end{split}\]

In alternative models of foam plasticity, the yield function is offset in the \(\bar{\sigma} - p\) plane along the pressure axis. To generalize the model, an offset yield surface centered at pressure \(p_0\) may be used in the form

(5.74)\[\hat{f}=\frac{\bar{\sigma}^2}{a^2}+\frac{(p-p_0)^2}{b^2}-1.\]

Note that with this form of the yield function, the component of the flow direction \(g^a_{ij}\) is now non-associative. This component is associative to the yield surface centered at the origin, but non-associative to the yield surface centered at \(p_0\).

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input.

  • The initial volume fraction of solid material in the foam, \(\varphi\), is defined with the PHI command line. For example, solid polyurethane weighs 75 pounds per cubic foot (pcf); uncompressed 10 pcf polyurethane foam would have a \(\varphi\) of \(0.133 = 10/75\).

  • The shear (deviatoric) strength of uncompressed foam is defined with the SHEAR STRENGTH command line.

  • The shear hardening modulus for the foam is defined with the SHEAR HARDENING command line.

  • The shear hardening exponent is defined with the SHEAR EXPONENT command line. The deviatoric strength is given by (SHEAR STRENGTH) + (SHEAR HARDENING) * PHI**(SHEAR EXPONENT).

  • The hydrostatic (volumetric) strength of the uncompressed foam is defined with the HYDRO STRENGTH command line.

  • The hydrodynamic hardening modulus is defined with the HYDRO HARDENING command line.

  • The hydrodynamic hardening exponent is defined with the HYDRO EXPONENT command line. The hydrostatic strength is given by (HYDRO STRENGTH) + (HYDRO HARDENING) * PHI**(HYDRO EXPONENT).

  • The prescription for non associated flow, \(\beta\), is defined with the BETA command line. When \(\beta = 0.0\), the flow direction is given by the normal to the yield surface (associated flow). When \(\beta = 1.0\), the flow direction is given by the stress tensor. It is recommended that associated flow \(\beta = 0.0\) be used for most analyses.

Output variables available for this model are listed in Table 5.22.

Table 5.22 State Variables for FOAM PLASTICITY Model (Section 5.2.23)

Name

Description

ITER

iterations

EVOL

volumetric strain

PHI

phi, \(\phi\)

EQPS

equivalent plastic strain, \(\bar{\varepsilon}^{p}\)

PA

\(A\)

PB

\(B\)

5.2.24. Low Density Foam Model

BEGIN PARAMETERS FOR MODEL LOW_DENSITY_FOAM
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  A    = <real>
  B    = <real>
  C    = <real>
  NAIR = <real>
  P0   = <real>
  PHI  = <real>
END [PARAMETERS FOR MODEL LOW_DENSITY_FOAM]

The low density foam material model is a phenomenological model for rigid, low density polyurethane foams. Development of this model followed extensive characterization efforts at Sandia National Laboratories with special emphasis placed on hydrostatic and triaxial compression tests [[35]]. A key observation of this investigation was the impact of trapped air inside the foam on the load bearing capabilities of the material.

In constructing a model describing the response of the low-density foams, Neilsen et al. [[35]] decomposed the response into that of the polymeric skeleton and the air such that,

(5.75)\[\sigma_{ij}=\sigma_{ij}^{\text{sk}} + \sigma^{\text{air}}\delta_{ij},\]

where the super script “sk” is used to refer to variables relating to the skeleton and “air” to the air. The contribution of the air component is only present, however, in constrained cases when the internal gases are trapped and not allowed to escape. If the foam material in not encased or encapsulated in someway, the air may escape and \(\sigma^{\text{air}}=0\). A model parameter, \(N_{\text{air}}\), is included to distinguish between these cases. If \(N_{\text{air}}\) is set to \(0\), the air pressure term is set to zero. For any other value, it is included.

Using the ideal gas law, it can be found that for an isothermal case,

(5.76)\[\sigma^{\text{air}}=\frac{p_{0}\varepsilon_{\text{V}}}{\varepsilon_{\text{V}}+1-\phi},\]

where \(p_{0}\), \(\varepsilon_{\text{V}}\), and \(\phi\) are the initial air pressure, volumetric strain, and the volume fraction of the solid (skeleton) material. Knowing the total stress of the material volume and air contribution, the skeleton stress may be found via (5.75). Furthermore, it should be noted that the foam (total) and skeleton strains are the same.

Based on their experimental observations, Neilsen et al. [[35]] noted a decoupling between the skeleton principal stresses. Therefore, the Poisson’s ratio of the skeleton is zero and that the yielding behavior in each principal direction is independent. A yield function of the form,

\[f_i=\sigma^{\text{sk}}_i-\bar{\sigma},\]

where \(f_i\) and \(\sigma^{\text{sk}}_i\) are the \(i^{th}\) yield function and skeleton principal stress, respectively, and

(5.77)\[\bar{\sigma} = A \left< I_{2}^{\prime} \right> + B \left( 1.0 + C \varepsilon_{V} \right)\]

with A, B, and C are material parameters, and \(\left< \cdot \right>\) denoting the Heaviside step function where

(5.78)\[\begin{split}\left< x \right> = \begin{cases} 0 \;\;\; \text{if } x \leq 0 \\ 1 \;\;\; \text{if } x > 0 \end{cases},\end{split}\]

was proposed. Additionally, \(I_{2}^{\prime}\) is the second invariant of the deviatoric strain. If a skeleton principal stress indicates yielding, it is set to the effective yield stress value, \(\bar{\sigma}\).

See Section 5.1.5 for more information on elastic constants input.

State variables for this model are listed in Table 5.23.

For more information on the low density foam material model, see [[35]].

Table 5.23 State Variables for LOW DENSITY FOAM Model (Section 5.2.24)

Name

Description

PAIR

Air pressure

5.2.25. Hyperfoam Model

BEGIN PARAMETERS FOR MODEL HYPERFOAM
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Strain energy density
  #
  N = <integer>
  SHEAR    = <real_list>
  ALPHA    = <real_list>
  POISSON  = <real_list>
END [PARAMETERS FOR HYPERFOAM]

The hyperfoam model is a hyperelastic model that can be used for modeling elastomeric foams. It is based on a strain energy with a form given by St"{o}rakers [[36]] which is similar to a form presented by Ogden [[37]]. The strain energy depends on the principal stretch ratios of the material and is given by

(5.79)\[W(\lambda_{k}) = \sum_{i=1}^{N} \frac{2\mu_{i}}{\alpha_{i}^{2}} \left[ \lambda_{1}^{\alpha_{i}} + \lambda_{2}^{\alpha_{i}} + \lambda_{3}^{\alpha_{i}} - 3 + \frac{1}{\beta_{i}}\left( J^{-\alpha_{i}\beta_{i}} - 1 \right) \right]\]

where \(\mu_{i}\) and \(\alpha_{i}\) are input parameters and \(J\) is the determinant of the deformation gradient. The value of \(\beta_{i}\) is calculated from the parameters \(\nu_{i}\) via

\[\beta_{i} = \frac{\nu_{i}}{1-2\nu_{i}}.\]

The \(\nu_{i}\) can be thought of as Poisson’s ratios, however in the context of the summation in (5.79) it is best to consider them as fitting parameters.

The strain energy (5.79) is a sum of \(N\) contributions. The principal Kirchoff stresses for the hyperfoam model, \(\tau_{k}\), can be calculated as

\[\tau_{k} = \lambda_{k}\frac{\partial W}{\partial\lambda_{k}}\]

which can be used to calculate the components of the Kirchoff stress, \(\tau_{ij}\), through

\[\tau_{ij} = \sum_{k=1}^3 \tau_{k}\hat{e}^{\,k}_{i}\hat{e}^k_{j}.\]

where \(\hat{e}^k_{i}\) are the components of the \(k^{\text{th}}\) eigenvector of the left stretch tensor in the global Cartesian coordinate system. The components of the Cauchy stress are then

(5.80)\[\sigma_{ij} = \frac{1}{J}\tau_{ij}.\]

Finally, it should be noted that the Hyperfoam model is also capable of reproducing the Blatz-Ko model [[38], [39]]. If only one term is chosen, \(N=1\), and \(\mu_{1} = \mu\), \(\alpha_{1} = -2\), and \(\nu_{1} = 0.25\) we get the Blatz-Ko strain energy density

\[W = \frac{\mu}{2} \left( \frac{I_{2}}{I_{3}} + 2\sqrt{I_{3}} - 5 \right)\;\;\; ,\]

where \(I_{2}\) and \(I_{3}\) are the second and third invariants of the right Cauchy-Green tensor.

  • See Section 5.1.5 for more information on elastic constants input.

  • The number of terms in the expansion of the strain energy is defined with the N command line.

  • The shear terms in the expansion of the strain energy, \(\mu_{i}\), are defined with the SHEAR command line.

  • The alpha terms in the expansion of the strain energy, \(\alpha_{i}\), are defined with the ALPHA command line.

  • The Poisson ratio terms in the expansion of the strain energy, \(\nu_{i}\), are defined with the POISSON command line.

There are no output variables available for this model.

5.2.26. Elastic Three-Dimensional Orthotropic Model

BEGIN PARAMETERS FOR MODEL ELASTIC_3D_ORTHOTROPIC
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Material coordinates system definition
  #
  COORDINATE SYSTEM             = <string> coordinate_system_name
  DIRECTION FOR ROTATION        = <real>   1|2|3
  ALPHA                         = <real>   (degrees)
  SECOND DIRECTION FOR ROTATION = <real>   1|2|3
  SECOND ALPHA                  = <real>   (degrees)
  #
  # Required parameters
  #
  YOUNGS MODULUS AA = <real>
  YOUNGS MODULUS BB = <real>
  YOUNGS MODULUS CC = <real>
  POISSONS RATIO AB = <real>
  POISSONS RATIO BC = <real>
  POISSONS RATIO CA = <real>
  SHEAR MODULUS AB  = <real>
  SHEAR MODULUS BC  = <real>
  SHEAR MODULUS CA  = <real>
  #
  # Thermal strain functions
  #
  THERMAL STRAIN AA FUNCTION = <string>
  THERMAL STRAIN BB FUNCTION = <string>
  THERMAL STRAIN CC FUNCTION = <string>
  #
END [PARAMETERS FOR MODEL ELASTIC_3D_ORTHOTROPIC]

The ELASTIC 3D ORTHOTROPIC model is an extension of the previously discussed ELASTIC routine and describes the linear elastic response of a material which exhibits orthotropic symmetry, where the orientation of the principal material directions can be arbitrary with respect to the global Cartesian axes as specified by the user.

First, a rectangular, cylindrical, or spherical reference coordinate system is defined. The material coordinate system can then be defined through two successive rotations about axes in the reference coordinate system. Refer to Section 5.1.7 for details on the definition of material coordinate systems. These principal axes are denoted as A, B, and C in the following. Thermal strains are also defined with respect to these principal material axes.

The elastic stiffness for an orthotropic material can be described in terms of the elastic compliance which relates the strain to the stress, \(\varepsilon_{ij} = \mathbb{S}_{ijkl}\sigma_{kl}\). For a material with an orthogonal ABC coordinate system, and written in that reference frame, the elastic compliance tensor is given by

(5.81)\[\begin{split}\left[ \tilde{\mathbb{S}} \right] = \begin{bmatrix} \frac{1}{E_{AA}} & -\frac{\nu_{BA}}{E_{BB}} & -\frac{\nu_{CA}}{E_{CC}} & 0 & 0 & 0 \\ \\ -\frac{\nu_{AB}}{E_{AA}} & \frac{1}{E_{BB}} & -\frac{\nu_{CB}}{E_{CC}} & 0 & 0 & 0 \\ \\ -\frac{\nu_{AC}}{E_{AA}} & -\frac{\nu_{BC}}{E_{BB}} & \frac{1}{E_{CC}} & 0 & 0 & 0 \\ \\ 0 & 0 & 0 & \frac{1}{2G_{AB}} & 0 & 0 \\ \\ 0 & 0 & 0 & 0 & \frac{1}{2G_{BC}} & 0 \\ \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2G_{CA}} \end{bmatrix},\end{split}\]

where the \(\tilde{\cdot}\) is used to denote a variable in the \(ABC\) material system.

From the definition (5.81), it can be seen that requiring symmetry leads to relations of the form,

\[\nu_{BA} = \nu_{AB}\frac{E_{BB}}{E_{AA}} \;\;\; ; \;\;\; \nu_{CB} = \nu_{BC}\frac{E_{CC}}{E_{BB}} \;\;\; ; \;\;\; \nu_{AC} = \nu_{CA}\frac{E_{AA}}{E_{CC}}.\]

Therefore, only 9 independent constants are needed to fully define the model behavior.

The orthotropic model is also formulated in a hypoelastic fashion, leading to a constitutive equation (in the ABC material frame) of,

\[\stackrel{\circ}{\tilde{\sigma}}_{ij} = \tilde{\mathbb{C}}_{ijkl}\left(\tilde{D}_{kl}-\tilde{D}^{th}_{kl}\right),\]

where \(\tilde{D}^{th}_{ij}\) is the thermal strain rate.

The elastic stiffness tensor, \(\tilde{\mathbb{C}}_{ijkl}\), is the inverse of the compliance, \(\tilde{\mathbb{C}}_{ijkl} = \tilde{\mathbb{S}}_{ijkl}^{-1}\), and as such may be determined to be,

\[\begin{split}\left[ \tilde{\mathbb{C}} \right] = \begin{bmatrix} \mathbb{C}_{AAAA} & \mathbb{C}_{AABB} & \mathbb{C}_{CCAA} & 0 & 0 & 0 \\ \\ \mathbb{C}_{AABB} & \mathbb{C}_{BBBB} & \mathbb{C}_{BBCC} & 0 & 0 & 0 \\ \\ \mathbb{C}_{CCAA} & \mathbb{C}_{BBCC} & \mathbb{C}_{CCCC} & 0 & 0 & 0 \\ \\ 0 & 0 & 0 & 2G_{AB} & 0 & 0 \\ \\ 0 & 0 & 0 & 0 & 2G_{BC} & 0 \\ \\ 0 & 0 & 0 & 0 & 0 & 2G_{CA} \end{bmatrix}.\end{split}\]

where

\[\begin{split}\mathbb{C}_{AAAA} & = \frac{1-\nu_{BC}\nu_{CB}}{\Delta}E_{AA} \;\;\; ; \;\;\; \mathbb{C}_{BBBB} = \frac{1-\nu_{CA}\nu_{AC}}{\Delta}E_{BB} \;\;\; ; \;\;\; \mathbb{C}_{CCCC} = \frac{1-\nu_{AB}\nu_{BA}}{\Delta}E_{CC} \nonumber \\ \\ \mathbb{C}_{AABB} & = \frac{\nu_{BA}+\nu_{CA}\nu_{BC}}{\Delta}E_{AA} \;\;\; ; \;\;\; \mathbb{C}_{BBCC} = \frac{\nu_{CB}+\nu_{AB}\nu_{CA}}{\Delta}E_{BB} \;\;\; ; \;\;\; \mathbb{C}_{CCAA} = \frac{\nu_{AC}+\nu_{BC}\nu_{AB}}{\Delta}E_{CC} \nonumber\end{split}\]

and \(\Delta = 1 - \nu_{AB}\nu_{BA} - \nu_{BC}\nu_{CB} - \nu_{CA}\nu_{RT} - 2\nu_{AB}\nu_{BC}\nu_{CA}\).

See [[40]] for more information about the elastic three-dimensional orthotropic model.

In the above command blocks all of the following are required inputs.

  • Even though they are not used within the material model itself, elastic constants are still required input for hourglass control, certain preconditioners, and other various capabilities. After examining various test problems, it has been determined that using the mean of the orthotropic properties as the isotropic elastic constants yields the best results. See Section 5.1.5 for more information on elastic constants input.

  • See Section 5.1.7 for more information on material coordinates system definition commands.

  • The Young’s moduli corresponding to the principal material axes A, B, and C are given by the YOUNGS MODULUS AA, YOUNGS MODULUS BB, and YOUNGS MODULUS CC command lines.

  • The Poisson’s ratio defining the BB normal strain when the material is subjected only to AA normal stress is given by the POISSONS RATIO AB command line.

  • The Poisson’s ratio defining the CC normal strain when the material is subjected only to BB normal stress is given by the POISSONS RATIO BC command line.

  • The Poisson’s ratio defining the AA normal strain when the material is subjected only to CC normal stress is given by the POISSONS RATIO CA command line.

  • The remaining Poisson’s ratios needed for the orthotropic elastic relations (i.e. the BA, CB, and AC Poisson’s ratios) are calculated internally. They are calculated as usual from the given Poisson’s ratios, given Young’s moduli, and energy considerations, which provide expressions for these parameters from the resulting symmetry of the compliance tensor.

  • The shear moduli for shear in the AB, BC, and CA planes are given by the SHEAR MODULUS AB, SHEAR MODULUS BC, and SHEAR MODULUS CA command lines, respectively

  • The thermal strain functions for normal thermal strains along the principal material directions are given by the THERMAL STRAIN AA FUNCTION, THERMAL STRAIN BB FUNCTION, and THERMAL STRAIN CC FUNCTION command lines.

Warning

The ELASTIC_3D_ORTHOTROPIC model cannot currently be used in conjunction with the control stiffness implicit solver block.

There are no output variables available for the Elastic Three-Dimensional Orthotropic material model.

5.2.27. Wire Mesh Model

BEGIN PARAMETERS FOR MODEL WIRE_MESH
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Yield surface parameters
  #
  YIELD FUNCTION = <string>
  TENSION        = <real>
END [PARAMETERS FOR MODEL WIRE_MESH]

The wire mesh model was developed at Sandia National Laboratories for use with layered sequences of metallic wire meshes and cloth fabric. Model development was based on an extensive series of experiments performed on these materials (see [[41]]) and used an existing model for rigid polyurethane foams as a starting point [[35]].

To be able to analyze the response of this material, the Cauchy stress tensor is first decomposed into its principal components, \(\sigma^i\). Each principal stress is evaluated independently and two behaviors are considered depending on whether or not the material is in tension or compression. Under a tensile load, the material is taken to be perfectly plastic above a yield stress, \(\tau\). For compressive loads, it is assumed that the materials hardens functionally with the volumetric engineering strain, \(\varepsilon_{\text{V}}\). In this formulation, an arbitrary form of this hardening function, \(\bar{\sigma}\left(\varepsilon_{\text{V}}\right)\) is assumed although in the original work [[41]],

(5.82)\[\bar{\sigma}\left(\varepsilon_{\text{V}}\right) = a e^{-b\varepsilon_{\text{V}}},\]

with \(a\) and \(b\) as material constants, was used.

With these assumptions, the yield function of the \(i^{\text{th}}\) principal stress, \(f^i\), may be written as,

\[\begin{split}f^i = \left\{\begin{array}{cc} \sigma^i-\tau, & \sigma^i \geq 0 \\ -\sigma^i-\bar{\sigma}\left(\varepsilon_{\text{V}}\right) & \sigma^i < 0 \end{array}\right. .\end{split}\]

where \(\tau\) is the isotropic tensile strength of the material.

Similar to the rigid polyurethane foam model [[41]], the flow rule is defined as:

\[d^{\text{p}}_{ij} = \dot{\gamma}^{1}P^{1}_{ijkl} \sigma_{kl} + \dot{\gamma}^{2}P_{ijkl}^{2}\sigma_{kl} + \dot{\gamma}^{3}P^{3}_{ijkl}\sigma_{kl}\]

with \(\dot{\gamma}^{i}\) being the magnitude of the \(i^{\text{th}}\) plastic strain increment and \(P^{r}_{ijkl}\) is the fourth-order principal projection operator defined as,

\[P^{r}_{ijkl} = n^{r}_i n^{r}_j n^{r}_k n^r_l\]

in which \(n^{r}_i\) is the corresponding direction vector of principal stress, \(\sigma^r\). With this definition,

\[\sigma^r=\sigma_{ij}P^r_{ijkl}\sigma_{kl}.\]

  • See Section 5.1.5 for more information on elastic constants input.

  • The yield function in compression is defined with the YIELD FUNCTION command line.

  • The tensile strength is give by the TENSION command line.

Output variables available for this model are listed in Table 5.24.

More information on the model can be found in the report by Neilsen, et. al. [[41]].

Table 5.24 State Variables for WIRE MESH Model (Section 5.2.27)

Name

Description

EVOL

engineering volumetric strain

YIELD

current yield strength in compression

5.2.28. Orthotropic Crush Model

BEGIN PARAMETERS FOR MODEL ORTHOTROPIC_CRUSH
  #
  # Elastic constants - Post lock-up
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  # Orthotropic Elastic properties - Pre-Crush
  #
  EX             = <real>
  EY             = <real>
  EZ             = <real>
  GXY            = <real>
  GYZ            = <real>
  GZX            = <real>
  #
  # Crush properties
  #
  CRUSH XX       = <string>
  CRUSH YY       = <string>
  CRUSH ZZ       = <string>
  CRUSH XY       = <string>
  CRUSH YZ       = <string>
  CRUSH ZX       = <string>
  VMIN           = <real>
  #
  # Post lock-up yield properties
  #
  YIELD STRESS   = <real>
  #
END [PARAMETERS FOR MODEL ORTHOTROPIC_CRUSH]

The orthotropic crush model in LAMÉ is designed to model the energy absorbing capability of crushable orthotropic materials, e.g. aluminum honeycomb, and is empirically based. The formulation follows that used for metallic honeycomb materials in LS-DYNA [[42]]. Three response regimes are assumed for this material: (i) orthotropic elastic, (ii) crush, and (iii) complete compaction (fully crushed). During the elastic regime, the model exhibits the response of an elastic, orthotropic material with all Poisson’s ratio equal to zero. After full compaction, the response is taken to be that of an isotropic, perfectly plastic material and the response between these two stages is tailored to smoothly transition between the two extremes. Crushing, incorporating both nonlinear elastic and plastic-like behaviors, is taken to begin as soon as volumetric contraction is noted (\(J=\det\left(F_{ij}\right)<1\)). As such, the purely elastic response is primarily seen during cyclic loadings in which the material is unloaded. An internal state variable, \(J_c\), is introduced to track the crushed state of the material and is defined as the minimum \(J\) over the entire deformation history such that,

\[J_c=\min_{t>0}\left[J\left(t\right)\right].\]

The crushing process manifests through two distinct behaviors: (i) the elastic properties scale linearly with the crush state from the initial orthotropic state to the of the final isotropic completely compacted material; and (ii) a plastic-like response is observed associated with corresponding crush curves (analogous to hardening curves).

Before complete compaction, the incremental constitutive relation may be written in terms of the rate of deformation tensor, \(D_{ij}\), as,

(5.83)\[\begin{split}\left\{ \begin{matrix} \stackrel{\circ}{\sigma}_{11} \\ \stackrel{\circ}{\sigma}_{22} \\ \stackrel{\circ}{\sigma}_{33} \\ \stackrel{\circ}{\sigma}_{12} \\ \stackrel{\circ}{\sigma}_{23} \\ \stackrel{\circ}{\sigma}_{31} \end{matrix} \right\} = \left[ \begin{matrix} \hat{E}_{11} & 0 & 0 & 0 & 0 & 0 \\ 0 & \hat{E}_{22} & 0 & 0 & 0 & 0 \\ 0 & 0 & \hat{E}_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & 2\hat{G}_{12} & 0 & 0 \\ 0 & 0 & 0 & 0 & 2\hat{G}_{23} & 0 \\ 0 & 0 & 0 & 0 & 0 & 2\hat{G}_{31} \end{matrix} \right] \left\{ \begin{matrix} D_{11} \\ D_{22} \\ D_{33} \\ D_{12} \\ D_{23} \\ D_{31} \end{matrix} \right\}\end{split}\]

where \(\hat{E}_{11}\), \(\hat{E}_{22}\), and \(\hat{E}_{33}\) are the normal stiffness and \(\hat{G}_{12}\), \(\hat{G}_{23}\), and \(\hat{G}_{31}\) are the shear stiffness. A clear decoupling between the different directional components is evident in (5.83). All six stiffness components are assumed to be functions of the current compaction level which may be defined as \(1-J_c\) and the evolution of these terms is responsible for crushing behavior \((*i*)\) alluded to previously.

The functional forms of the stiffness are given by,

(5.84)\[\begin{split}\hat{E}_{\beta} & = E_{\beta}+\alpha\left(E-E_{\beta}\right)\qquad\qquad \beta=11, 22, 33 \nonumber \\ & \nonumber \\ \hat{G}_{\gamma} & = G_{\gamma}+\alpha\left(G-G_{\gamma}\right)\qquad\qquad \gamma=12, 23, 31,\end{split}\]

where \(E\) and \(G\) are the Young’s and shear moduli, respectively, of the fully compacted material while \(E_{\beta}\) and \(G_{\gamma}\) are the input orthotropic elastic stiffness components of the virgin, uncompacted material. It is assumed that these stiffness vary linearly between the pre- and post-compacted material such that,

\[\alpha=\frac{\left(1-J_c\right)}{V_{min}},\]

with \(V_{min}\) being the minimum relative volume (or maximum compaction).

With respect to the second behavior observed during crushing, a plastic-like response governed by crush curves is observed. Given the decoupling between the different stresses and deformations, a crush curve needs to be defined for each of the six normal and shear stresses. An example of such a curve is presented in Fig. 5.10, and three distinct regions are evident. Initially, at low compaction levels, a plateau is observed. This plateau is essentially an initial crush strength and prior to this stress level all nonlinear deformations associated with material compaction manifest through changes in the respective moduli. When the stress reaches the specified levels, however, the curves play a role analogous to the hardening curve and the material stress follows the curve. Physically, the plateau is associated with crushing the internal honeycomb or foam structure of the material. As the material approaches full compaction and microstructural contact effects become important, a sharp rise in the stress is noted (see \(\approx 0.6\leq 1-J_c\leq0.7=V_{min}\) in Fig. 5.10). After complete compaction another plateau corresponding to perfect plasticity is evident.

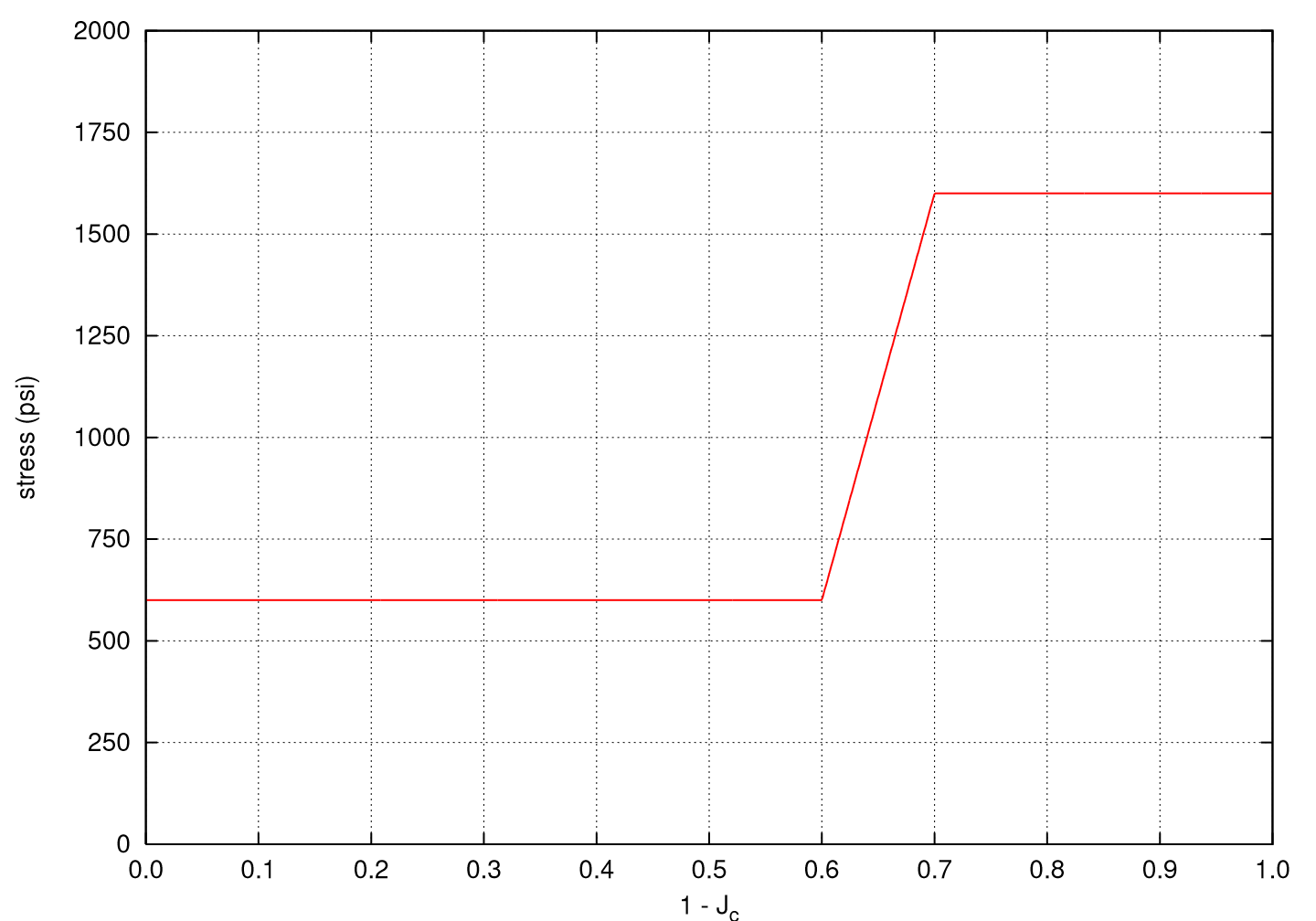
../../_images/crush.png

Fig. 5.10 An example of an input crush curve for an aluminum honeycomb.

Above some value of compaction (\(1-J_c=V_{min}\)), the material will be fully compacted and behave as an elastic, perfectly plastic material. The fully compacted response is given by the Young’s modulus, \(E\), Poisson’s ratio, \(\nu\), and the yield stress, \(\sigma_{y}\). Details of this response may be found in previous sections on the various elastic-plastic models (e.g. Section 5.2.5).

In the above command blocks:

  • The EX, EY, EZ, GXY, GYZ, and GZX command lines define, respectively, the initial, pre-crush directional moduli \(E_{xx}\), \(E_{yy}\), \(E_{zz}\), \(G_{xy}\), \(G_{yz}\), and \(G_{zx}\) from (5.83).

  • CRUSH XX, YY, ZZ, XY, YZ, and ZX inputs require the name of a function defined via a FUNCTION command line in the SIERRA scope. These functions describe the directional crush characteristics of the material and give the current stress value (in a direction) as a function of the current compaction (\(1-J_c\)).

  • The command VMIN defines the minimum relative volume of the material that is achieved when the material is completely crushed. This parameter may also be considered as the maximum compaction.

  • The elastic constant commands refer to the post lock-up, fully compacted isotropic response of the material. See Section 5.1.5 for more information on elastic constants input.

  • YIELD STRESS refers to the plateau stress of the material after lock-up when the response is perfectly plastic.

Output variables available for this model are listed in Table 5.25. For information about the orthotropic crush model, consult [[42]].

Table 5.25 State Variables for ORTHOTROPIC CRUSH Model (Section 5.2.28)

Name

Description

CRUSH

current (unrecoverable) compaction/relative volume

5.2.29. Orthotropic Rate Model

BEGIN PARAMETERS FOR MODEL ORTHOTROPIC_RATE
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  YIELD STRESS = <real>
  #
  MODULUS TTTT = <real>
  MODULUS TTLL = <real>
  MODULUS TTWW = <real>
  MODULUS LLLL = <real>
  MODULUS LLWW = <real>
  MODULUS WWWW = <real>
  MODULUS TLTL = <real>
  MODULUS LWLW = <real>
  MODULUS WTWT = <real>
  #
  TX = <real>
  TY = <real>
  TZ = <real>
  LX = <real>
  LY = <real>
  LZ = <real>
  #
  MODULUS FUNCTION = <string>
  RATE FUNCTION    = <string>
  #
  T FUNCTION  = <string>
  L FUNCTION  = <string>
  W FUNCTION  = <string>
  TL FUNCTION = <string>
  LW FUNCTION = <string>
  WT FUNCTION = <string>
END [PARAMETERS FOR MODEL ORTHOTROPIC_RATE]

The orthotropic rate model extends the functionality of the orthotropic crush constitutive model described in Section 5.2.28. The orthotropic rate model has been developed to describe the behavior of an aluminum honeycomb subjected to large deformation. The orthotropic rate model, like the original orthotropic crush model, has six independent yield functions that evolve with volume strain. Unlike the orthotropic crush model, the orthotropic rate model has yield functions that also depend on strain rate. The orthotropic rate model also uses an orthotropic elasticity tensor with nine elastic moduli in place of the orthotropic elasticity tensor with six elastic moduli used in the orthotropic crush model.

A honeycomb orientation capability is included with the orthotropic rate model, allowing users to prescribe initial honeycomb orientations that are not aligned with the original global coordinate system. The three material directions are defined as follows: The T-direction is usually associated with the generator axis for the honeycomb, the L-direction is in the ribbon plane (defined by flat sheets used in reinforced honeycomb) orthogonal to the generator axis, and the W-direction is orthogonal to the ribbon plane.

In the above command blocks:

  • For the ORTHOTROPIC_RATE model, only YOUNGS MODULUS needs to be defined; this is the Young’s modulus in the fully compacted state. If two other elastic constants are provided, they will be used to define the fully compacted Young’s modulus. See Section 5.1.5 for more information on elastic constants input.

  • The YIELD STRESS command line defines the yield stress of the fully compacted honeycomb.

  • The nine elastic moduli for the orthotropic, uncompacted honeycomb are defined with respect to each material direction using the MODULUS TTTT, MODULUS TTLL, MODULUS TTWW, MODULUS LLLL, MODULUS LLWW, MODULUS WWWW, MODULUS TLTL, MODULUS LWLW, and MODULUS WTWT command lines.

  • The components of vectors defining the T- and L-directions of the honeycomb are specified using the TX, TY, and TZ, and LX, LY, and LZ command lines, respectively. The vector component values tx, ty, and tz define the orientation of the honeycomb’s T-direction (generator axis), while lx, ly, and lz define the orientation of the L-direction. The vectors T and L are defined in the global coordinate system and must be orthogonal.

  • The function describing the variation in moduli with compaction is given by the MODULUS FUNCTION command line. The moduli vary continuously from their initial orthotropic values to isotropic values when full compaction is obtained.

  • The function describing the change in strength with strain rate is given by the RATE FUNCTION command line. Note that all strengths are scaled with the multiplier obtained from this function.

  • The function describing the T-normal strength of the honeycomb as a function of compressive volumetric strain is given by the T FUNCTION command line.

  • The function describing the L-normal strength of the honeycomb as a function of compressive volumetric strain is given by the L FUNCTION command line.

  • The function describing the W-normal strength of the honeycomb as a function of compressive volumetric strain is given by the W FUNCTION command line.

  • The function describing the TL-normal strength of the honeycomb as a function of compressive volumetric strain is given by the TL FUNCTION command line.

  • The function describing the LW-normal strength of the honeycomb as a function of compressive volumetric strain is given by the LW FUNCTION command line.

  • The function describing the WT-normal strength of the honeycomb as a function of compressive volumetric strain is given by the WT FUNCTION command line.

Note that several of the command lines in this command block reference functions. These functions must be defined in the SIERRA scope.

Output variables for this model are listed in Table 5.26.

Table 5.26 State variables for ORTHOTROPIC RATE Model (Section 5.2.29)

Index

Name

Variable Description

1

CRUSH

minimum volume ratio, crush is unrecoverable \(\left(\hat{\varepsilon}_{V}\right)\) \

Warning

Strongly rate-dependent models may fare poorly in implicit quasistatic solution. In implicit analyses the rate term used to evaluate the current load step is the rate seen by the model in the previous load step. This may cause the solution to oscillate between high- and low-rate equilibrium states from step to step.

5.2.30. Plane Stress Rate Plasticity

BEGIN PARAMETERS FOR MODEL PLANE_STRESS_RATE_PLASTICITY
   #
   # Elastic constants
   #
   YOUNGS MODULUS = <real>
   POISSONS RATIO = <real>
   SHEAR MODULUS  = <real>
   BULK MODULUS   = <real>
   LAMBDA         = <real>
   TWO MU         = <real>
   #
   # Optional parameters related to inelastic correction criteria
   #
   TOLERANCE          = <real> tolerance (1.0e-10)
   MAX_INEL_CORR_ITER = <int> maximum_correction_iterations (100)
   MAX_LS_CORR_ITER   = <int> maximum_line_search_cutbacks  (20)
   #
   USER RATE DEPENDENCE = 0|1(0)
   YIELD STRESS         = <real>
   #
   FORMULATION          = <int> formulation (1)
   #
   # Input Options for USER RATE DEPENDENCE = 0
   #
   # linear hardening
   HARDENING MODULUS = <real> hardening_modulus
   # power law hardening
   HARDENING CONSTANT = <real> hardening_constant
   HARDENING EXPONENT = <real> hardening_exponent (0.5)
   # multilinear hardening
   HARDENING FUNCTION = <string>
   #
   # Rate dependence
   #
   # Johnson-Cook rate dependence
   RATE CONSTANT = <real>
   # multilinear rate dependence
   RATE FUNCTION = <string> rate_function_name
   #
   # Input Options for USER RATE DEPENDENCE = 1
   #
   # rate-dependent yield
   YIELD STRAIN RATES = <real_list> yield_strain_rates
   YIELD CURVES       = <string_list> yield_function_names
   # rate-dependent damage
   FRACTURE STRAIN RATES = <real_list> fracture_strain_rates
   FRACTURE CURVES       = <string_list> fracture_function_names
   DECAY COEFFICIENT     = <real> (1.0)
   #
   # Thermal softening commands (Johnson-Cook)
   INITIAL TEMPERATURE   = <real>
   MELT TEMPERATURE      = <real>
   REFERENCE TEMPERATURE = <real>
   THERMAL EXPONENT      = <real>
   #
END [PARAMETERS FOR MODEL PLANE_STRESS_RATE_PLASTICITY]

The plane stress rate plasticity model is the plane stress formulation of a \(J_2\) plasticity model given by Simo and Taylor [[43]] (and described again in Simo and Hughes [[5]]) extended to include rate-dependent hardening and a failure model for use with shell elements.

Like other plasticity models, the components of the objective stress rate, \(\stackrel{\circ}{\sigma}_{ij}\), are written as,

\[\stackrel{\circ}{\sigma}_{ij} = \mathbb{C}_{ijkl}D_{kl}^{\text{e}}\]

where \(\mathbb{C}_{ijkl}\) are the components of the fourth-order, isotropic elasticity tensor and \(D_{ij}^{\text{e}}\) are the components of the elastic part of the total rate of deformation tensor. An additive split of the total rate of deformation tensor into elastic and plastic contributions is assumed such that,

\[D_{ij}=D_{ij}^{\text{e}}+D_{ij}^{\text{p}}.\]

The plane stress formulation recasts the three-dimensional problem into a constrained subspace with plane stress conditions acting as the constraints. To do this, the plane stress rate plasticity model follows the approach of Simo and Taylor [[43]] to enforce \(\sigma_{13}=\sigma_{23}=\sigma_{33}=0\) and related conditions.

For the plasticity portion of the model, the formulation of Simo and Taylor [[43]] is usedfootnote{In the work of Simo and Taylor [[43]] (and later Simo and Hughes [[5]]) hardening is assumed to be rate and temperature independent. Here, such terms are included but do not materially change the formulation. Similarly, the earlier works also introduce kinematic hardening which is not used in the current model.} in which a traditional three-dimensional \(J_2\) plasticity model is recast in reduced subspace. To do this, it is recalled that in three-dimensions the von Mises effective stress, \(\phi\), is written,

\[\phi^2=\frac{3}{2}s_{ij}s_{ij},\]

with \(s_{ij}=\sigma_{ij}-(1/3)\sigma_{kk}\delta_{ij}\) the deviatoric stress. To write an equivalent expression in the reduced subspace, the vector, \(\underline{\sigma}\), and matrix, \(\underline{\underline{\bar{P}}}\), are introduced asfootnote{Note, here the \(\underline{x}\) and \(\underline{\underline{X}}\) notations are introduced for vector and matrix objects, respectively, to clearly distinguish that these variables are not tensors. This results from operating in the constrained stress subspace and means that these terms do not have properties of a tensor and act on each other as traditional matrices and vectors.},

\[\begin{split}\underline{\sigma}=\left[\begin{array}{c}\sigma_{11} \\ \sigma_{22} \\ \sigma_{12} \end{array}\right], \qquad ; \qquad \underline{\underline{\bar{P}}}=\frac{1}{3}\left[\begin{array}{ccc}2 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & 3\end{array}\right],\end{split}\]

such that,

\[\begin{split}\underline{s}=\left[\begin{array}{c} s_{11} \\ s_{22} \\ s_{12} \end{array}\right] = \underline{\underline{\bar{P}}}\;\underline{\sigma}.\end{split}\]

In the reduced plane-stress subspace, an alternative effective stress, \(\bar{\phi}\), is given as,

\[\bar{\phi}^2=\underline{\sigma}^T\underline{\underline{P}}\;\underline{\sigma}=\frac{2}{3}\phi^2,\]

where

\[\begin{split}\underline{\underline{P}}=\frac{1}{3}\left[\begin{array}{ccc}2 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & 6\end{array}\right],\end{split}\]

in which \(\underline{\underline{P}}\) and \(\underline{\underline{\bar{P}}}\) differ by a two in the shear term to reflect Voigt corrections.

A yield function, \(f\), is introduced as,

(5.85)\[f=\bar{\phi}^2-R^2,\]

with,

\[R = \sqrt{\frac{2}{3}}\bar{\sigma}\left(\bar{\varepsilon}^p,\dot{\bar{\varepsilon}}^p,\theta\right),\]

where \(\bar{\varepsilon}^p\) and \(\dot{\bar{\varepsilon}}^p\) are the equivalent plastic strain (isotropic hardening variable) and its rate, respectively. Various hardening options may be used with this model. In general, the current flow stress is written as,

(5.86)\[\bar{\sigma}\left(\bar{\varepsilon}^p,\dot{\bar{\varepsilon}}^p,\theta\right)=\left(\sigma_y + K\left(\bar{\varepsilon}^p\right)\right) \hat{\sigma}\left(\dot{\bar{\varepsilon}}^p\right)\left(1-\left(\frac{\theta-\theta_{\text{ref}}}{\theta_{\text{melt}}-\theta_{\text{ref}}}\right)^M\right),\]

in which \(\sigma_y\) is the original yield stress, \(K\) is the isotropic hardening function that may take linear, power-law, or multilinear form, \(\hat{\sigma}\) the rate multiplier whose specification will be defined later, and the right-most term is the Johnson-Cook temperature dependence term that may be optionally used to give temperature dependence of the flow-stress.

To complete the theoretical formulation, the flow rules are specified as,

\[\begin{split}d\underline{\varepsilon}^p & = \lambda\underline{\underline{P}} \; \underline{\sigma}, \\ d\bar{\varepsilon}^p & = \dot{\bar{\varepsilon}}^{p}\Delta t = \lambda\sqrt{\frac{2}{3}}\phi,\end{split}\]

where \(\lambda\) is the consistency multiplier enforcing \(f=0\) during plastic deformation and \(d\underline{\varepsilon}^p\) is the plastic strain increment in the constrained subspace. It is emphasized here that the yield surface described in (5.85) is not homogeneous of degree one like in other three-dimensional formulations presented in this manual. As such, the consistency multiplier and equivalent plastic strain increment are not equivalent. As an example of this, by consideration of the preceding relations, it is apparent that \(\lambda\) has units of one over stress.

The specification of the rate dependence, \(\hat{\sigma}\), is important as it enables the consideration of two different model responses. These behaviors are controlled via the USER RATE DEPENDENCE command. If this input parameter is zero, then either an analytical or user-defined rate-dependence may be given. Importantly, in this case failure is not modeled. For the analytical case, the Johnson-Cook [[8], [9]] rate-multiplier is used such that,

\[\begin{split}\hat{\sigma}\left(\dot{\bar{\varepsilon}}^p\right)=\left\{\begin{array}{cc} 1+C\ln\left(\frac{\dot{\bar{\varepsilon}}^p}{\dot{\bar{\varepsilon}}_0}\right) & \dot{\bar{\varepsilon}}^p > \dot{\bar{\varepsilon}}_0 \\ 1 & \dot{\bar{\varepsilon}}^p \leq \dot{\bar{\varepsilon}}_0 \end{array}\right. ,\end{split}\]

with \(C\) being the rate dependence multiplier and \(\dot{\bar{\varepsilon}}_0\) is a reference rate. Note, while other models allow user specification of the reference rate, the plane stress rate plasticity model uses the value set in the original work of Johnson-Cook [[8]] such that \(\dot{\bar{\varepsilon}}_0=1 \text{s}^{-1}\). Alternatively, a user function may be specified for the rate multiplier, \(\hat{\sigma}\).

If USER RATE DEPENDENCE is set to one, both rate dependence and failure may be modeled. With respect to the rate dependence, (5.86) is rewritten,

\[\bar{\sigma}\left(\bar{\varepsilon}^p,\dot{\bar{\varepsilon}}^p,\theta\right)=\tilde{\sigma}\left(\bar{\varepsilon}^p,\dot{\bar{\varepsilon}}^p\right) \left(1-\left(\frac{\theta-\theta_{\text{ref}}}{\theta_{\text{melt}}-\theta_{\text{ref}}}\right)^M\right),\]

in which both isotropic hardening and rate dependence are described via definition of \(\tilde{\sigma}\). In this case, \(\tilde{\sigma}\) can*not* be specified through analytical expressions and must instead be given as a series of isotropic hardening curves; each at a different strain rate. For rates not explicitly given, interpolation is performed between relevant curves. Note, no extrapolation is performed with respect to the rates. If a rate is determined outside any specified curves, the hardening is calculated with respect to the bounding curve.

For failure, a failure parameter, \(\alpha\), is calculated as

\[\alpha=\int_0^t \frac{1}{\varepsilon_f\left(\eta,\dot{\bar{\varepsilon}}^p\right)}\dot{\bar{\varepsilon}}^pdt = \sum_{t_0}^{t}\frac{d\bar{\varepsilon}^p}{\varepsilon_f\left(\eta,\dot{\bar{\varepsilon}}^p\right)},\]

in which the summation is used to imply the discrete calculation of the damage variable over a series of loadsteps and \(\varepsilon_f\) is the rate and triaxiality, \(\eta\), dependent failure strain. The failure strain, \(\varepsilon_f\), is specified in a fashion similar to \(\tilde{\sigma}\). Specifically, a series of triaxiality dependent functions are defined each at a given strain rate. Interpolation is used at rates between those specified. Extrapolation outside the defined bounds is not done and the extremum curves are instead used.

The onset of damage is assumed to occur when \(\alpha = 1\) and the current failure strain is taken to be the critical one such that \(\varepsilon_f^{cr}=\varepsilon_f\left(t=t_{cr}\right)\) with \(t_{cr}\) being the time at which \(\alpha=1\). Subsequent damage calculation is performed via,

\[\alpha\left(t>t_{cr}\right)=\int_{0}^{t_{cr}}\frac{1}{\varepsilon_f\left(\eta,\dot{\bar{\varepsilon}}^p\right)}\dot{\bar{\varepsilon}}^pdt + \int_{t_{cr}}^{t}\frac{1}{\varepsilon_f^{cr}}\dot{\bar{\varepsilon}}^pdt.\]

After the critical failure parameter has been reached, an exponential decay relation is used to decrease the strength of the material. In this fashion, a decay relation of the form,

\[\bar{\sigma}=\bar{\sigma}e^{C_1\left(1-\alpha\right)},\]

is used in which \(C_1\) is the decay coefficient.

For more information about the plane stress rate plasticity model, consult [[43], [5]].

In the command blocks that define the Plane Stress Rate Plasticity model:

  • See Section 5.1.5 for more information on elastic constants input.

  • TOLERANCE specifies the numerical value used for assessing convergence of the plastic correction routine.

  • Optionally, the user can specify the maximum number of inelastic correction iterations for the plasticity inelastic correction routines. By default this value is 100.

  • Optionally, the user can specify the maximum number of line search cutbacks in the plasticity correction routine. By default this value is 20 and only impacts the formulation not equal to 0 (plastic strain rate) case.

  • The reference nominal yield stress, \(\bar{\sigma}\), is defined with the YIELD STRESS command line.

  • The formulation parameter defines whether the total strain rate (formulation = 0) or equivalent plastic strain rate (anything else) is used for calculating rate dependence.

  • INITIAL TEMPERATURE defines the initial temperature at \(t=0\).

  • MELT TEMPERATURE defines \(T_{melt}\) in (5.86).

  • REFERENCE TEMPERATURE defines \(T_{ref}\) in (5.86).

  • THERMAL EXPONENT defines \(M\) in (5.86).

  • The USER RATE DEPENDENCE is used to control the way hardening may be specified and whether or not failure is calculated.

    • For USER RATE DEPENDENCE = 0, plastic hardening may be specified as linear, power-law, OR multilinear. Failure cannot be used with USER RATE DEPENDENCE = 0:

      • For linear hardening, a non-zero HARDENING MODULUS should be specified. Do not give if using power-law or multilinear hardening.

      • For power-law hardening, the HARDENING CONSTANT should be specified. Optionally, the HARDENING EXPONENT parameter should be specified if the default value (0.5) is not to be used. Do not give for linear or multilinear hardening.

      • For multilinear hardening, a function name should be given for HARDENING FUNCTION command. Do not specify for linear or power-law hardening.

      • For Johnson-Cook rate-dependence, a rate constant must be specified via the RATE CONSTANT command. Do not use if using functionally specified rate-dependence.

      • For functionally defined rate-dependence, a function name should be given via the RATE FUNCTION command. Do not specify if using Johnson-Cook type rate dependence.

    • For USER RATE DEPENDENCE = 1, plastic hardening is specified through a series of user functions. Failure can be modeled with USER RATE DEPENDENCE = 1:

      • Rate-dependent plastic hardening is specified jointly via the YIELD STRAIN RATES and YIELD CURVES commands. YIELD STRAIN RATES is a list of strain rates corresponding one-to-one to functions specified in the YIELD CURVES list of strings giving user-defined function names. Each YIELD CURVES function should give the plastic isotropic plastic hardening curve at the corresponding rate given in YIELD STRAIN RATES.

      • Failure strains used in calculating damage are specified via the FRACTURE STRAIN RATES and FRACTURE CURVES commands. Similarly to the plastic hardening, a list of strain rates should be given with the FRACTURE STRAIN RATES input. Each rate should correspond one-to-one with a user function listed via FRACTURE CURVES. These functions are specified as a function of triaxiality and should give the failure strain at the specified rate.

      • The decay coefficient, \(C_1\), that controls the exponential decay of the yield stress related to failure should be specified via the DECAY COEFFICIENT command.

Output variables available for this model are listed in Table 5.27.

Table 5.27 State Variables for PLANE STRESS RATE PLASTICITY Model (Section 5.2.30)

Name

Description

EQPS

equivalent plastic strain, \(\bar{\varepsilon}^{p}\)

EQDOT

equivalent plastic strain rate, \(\dot{\bar{\varepsilon}}^{p}\)

SEFF

effective stress, \(\phi\)

Warning

Strongly rate-dependent models may fare poorly in implicit quasistatic solution. In implicit analyses the rate term used to evaluate the current load step is the rate seen by the model in the previous load step. This may cause the solution to oscillate between high- and low-rate equilibrium states from step to step.

5.2.31. Incompressible Solid Model

BEGIN PARAMETERS FOR MODEL INCOMPRESSIBLE_SOLID
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  #
  #
  K SCALING = <real>k_scaling
  2G SCALING = <real>2g_scaling
  TARGET E = <real>target_e
  MAX POISSONS RATIO = <real>max_poissons_ratio
  REFERENCE STRAIN = <real>reference_strain
  SCALING FUNCTION = <string>scaling_function_name
END [PARAMETERS FOR MODEL INCOMPRESSIBLE_SOLID]

The incompressible solid model is a variation of the elastic model and can be used in both Presto and Adagio. In Adagio, the incompressible solid model is used with the control-stiffness option in the multilevel solver. The control-stiffness option is implemented via the CONTROL STIFFNESS command block and is discussed in Section 4. The model is used to model nearly incompressible materials where Poisson’s ratio, \(\nu\), \(\approx 0.5\). In the course of solving a series of model problems in Adagio, the material response from this model incorporates scaling the bulk and/or shear behaviors to yield a material response that is more amenable to solution using Adagio’s conjugate gradient solver. The final material behavior that is calculated corresponds to the actual moduli that are specified. When this model is used in Presto, the material scalings are ignored, and the model behaves like a linear elastic model.

In the above command blocks, the following definitions are applicable. Usage requirements are identified both in this list of definitions and in the discussion that follows the list.

  • See Section 5.1.5 for more information on elastic constants input.

  • The following material-scaling command lines are used only in Adagio and are optional as described below: - The nominal bulk scaling is defined with the K SCALING command line. - The nominal shear scaling is defined with the 2G SCALING command line. - The target Young’s modulus is defined with the TARGET E command line. - The maximum Poisson’s ratio is defined with the MAX POISSONS RATIO command line. - The reference strain is defined with the REFERENCE STRAIN command line. - The SCALING FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes the time dependent scaling to be applied.

As noted previously, only two of the elastic constants are required to define the unscaled material response. This requirement applies to use of the incompressible solid model in Presto and in Adagio. Further, all the material-scaling command lines are only used in Adagio.

Several options exist for defining the bulk and/or shear scalings that can be used with the multilevel solver in Adagio.

  • Option 1: You can provide the scalings directly by including both of the K SCALING and 2G SCALING command lines or either of them. When both command lines are input, the user-specified values for their parameters will be used. If only the K SCALING command line is input, the bulk scaling is as specified in the k_scaling parameter, and the value of the shear scaling parameter, 2g_scaling, is set to 1.0. On the other hand, if only the 2G SCALING command line is input, then the shear scaling is as specified in the 2g_scaling parameter, but the value of the bulk-scaling parameter, k_scaling, is not set to 1.0. Instead, the bulk scaling is determined by computing a scaled bulk modulus from the scaled shear modulus and a (scaled) Poisson’s ratio of 0.3. Then, the bulk scaling is determined as the ratio of the scaled bulk modulus to the actual bulk modulus.

  • Option 2: You can specify either or both of the TARGET E and MAX POISSONS RATIO command lines to define the scalings. If only the TARGET E command line is included, the bulk and shear scalings are computed by first finding scaled moduli using the value of the target_e parameter along with a (scaled) Poisson’s ratio of 0.3. The bulk and shear scalings are then determined as the ratio of the appropriate scaled to unscaled modulus. If only the MAX POISSONS RATIO command line is included, the shear scaling is set to 1.0, and the bulk scaling is computed by first calculating a scaled bulk modulus from the actual shear modulus and the value of the max_poissons_ratio parameter. The bulk scaling is then calculated as the ratio of the scaled bulk modulus to the actual bulk modulus. If both the TARGET E and MAX POISSONS RATIO command lines are included, the bulk scaling (and shear scaling) is determined from the ratio of the bulk scaled modulus (and shear scaled modulus) computed using the values of the target_e and max_poissons_ratio parameters to the unscaled bulk (and shear) modulus.

  • Option 3: You can choose not to include any of the K SCALING, 2G SCALING, TARGET E, and MAX POISSONS RATIO command lines. In such case, the shear scaling is set to 1.0, and the bulk scaling is computed as the ratio of the scaled bulk modulus coming from the real shear modulus and a (scaled) Poisson’s ratio of 0.3 to the actual bulk modulus.

The function referenced by the value of the parameter scaling_function_name in the SCALING FUNCTION command line can be used to modify the bulk and shear scalings in solution time. The actual scalings used are computed by taking the scalings specified by the parameter values in the K SCALING, 2G SCALING, TARGET E, and MAX POISSONS RATIO command lines and multiplying them by the function value at the specified solution time. If the SCALING FUNCTION command line is not included, the bulk and shear scalings are fixed in time.

The REFERENCE STRAIN command line supplies a value for the reference strain that is used to create a normalized material constraint violation based on strains. Specifying a reference strain implies the use of strains for measuring the material constraint violation (or part of the control-stiffness error in Adagio). Otherwise, the material constraint violation is determined by using the change in the scaled stress response over the current model problem.

5.2.32. Universal Polymer Model

The UPM model is commonly used in one of two ways. The most general use case is portrayed in full in the following syntax in which the user specifies both Prony series explicitly. That is, the user specifies all Prony relaxation times (\({\tau}\)) and weights for both the thermal/volumetric (\({f_v}\)) and shear (\({f_s}\)) relaxation functions. Note that in the UPM model, only a single set of Prony relaxation times can be specified and acts as the basis for both relaxation spectra. In other words, a single set of relaxation times is specified, and both functions use their own (distinct) weights.

Default parameters are not set. Any system of units can be used with the model. There are no internalunits assumptions.

BEGIN PARAMETERS FOR MODEL UNIVERSAL_POLYMER
  #
  # Elastic constants: These Should be Set to the Glassy Moduli
  #                    for robustness considerations
  #
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  #
  ## Reference Temperature and Material CLOCK Parameters
  #
  REFERENCE TEMPERATURE   = <real> # Temperature
  STRESS FREE TEMPERATURE = <real>  # Temperature
  #
  WLF C1   = <real>
  WLF C2   = <real> # Temperature
  CLOCK C3 = <real> # Temperature
  CLOCK C4 = <real> # Temperature
  #
  ## Glassy and Rubbery Moduli
  #  and CTE Definitions at the Reference Temperature
  #
  BULK GLASSY 0    = <real> # Units of Pressure
  BULK RUBBERY 0   = <real> # Units of Pressure
  SHEAR GLASSY 0   = <real> # Units of Pressure
  SHEAR RUBBERY 0  = <real> # Units of Pressure
  VOLCTE glassy 0  = <real> # Units of Inverse Temperature
  VOLCTE rubbery 0 = <real> # Units of Inverse Temperature
  #
  FILLER VOL FRACTION = <real>
  #
  ## Relaxation Time Spectra Definitions
  #
  WWBETA 1 = <real>
  WWTAU 1  = <real> # Units of time
  WWBETA 2 = <real>
  WWTAU 2  = <real> # Units of time
  #
  SPECTRUM START TIME = <real>  # Units of time
  SPECTRUM END TIME   = <real>  # Units of time
  LOG TIME INCREMENT  = <real>  # Units of time
  #
  ## Direct Prony Spectra Inputs
  #
  RELAX TIME 1 = <real>  # Unit of time
  RELAX TIME 2 = <real>
  .
  RELAX TIME 30 = <real>
  #
  ## Thermal/Volumetric Relaxation Spectrum Prony Weights
  #
  F1 1 = <real>
  F1 2 = <real>
  .
  F1 30 = <real>
  #
  ## Shear Relaxation Spectrum Prony Weights
  #
  F2 1 = <real>
  F2 2 = <real>
  .
  F2 30 = <real>
 END [PARAMETERS FOR MODEL UNIVERSAL_POLYMER]

Not all Prony spectra/weight parameter pairs (1-30) need to be specified. Only those specified will be used, and the ones not specified will be set to zero. Prony weights for each relaxation function should sum to 1.0, or the model will rescale the weights so that they do sum to one. This rescaling will change the underlying relaxation response.

When the model is used with both relaxation functions being specified directly, then the parameters: SPECTRUM START TIME, SPECTRUM END TIME, LOG TIME INCREMENT, WW TAU (1,2), and WW BETA (1,2) must be specified as 0 to avoid errors during the model property check. Note (1) is associated with the thermal/volumetric function, and (2) is associated with the shear relaxation function.

Another common usage of the UPM model is to specify the Williams-Watts (KWW) stretched exponential \(\tau, \beta\) parameters for either or both relaxation functions (1 and/or 2) corresponding to the function \(f=\exp(-(t/\tau)^\beta)\). That is, a set of Prony weights, \(w_i\) corresponding to a specific set of Prony times, \(\tau_i\), will be found during the model property check routine. If the other relaxation function is directly specified as above, then the Prony times from the directly specified relaxation spectrum are used. In this case, the Prony weights for the relaxation function being fit to the KWW function are found through a Least-Squared Error minimization routine built into the UPM model over a discretely sampled set of times between the minimum and maximum Prony times.

When neither Prony spectrum is directly specified (both will be fit to KWW functions), then the Prony times (for both relaxation functions) are determined from an evenly logarithmically spaced set of Prony times beginning with the SPECTRUM START TIME and ending with the SPECTRUM END TIME and spaced with the (base 10) LOG TIME INCREMENT. For each relaxation function that is fit with the UPM model to a KWW function, the WW TAU (1,2) and WW BETA (1,2) parameters must be specified. However, if the user specifies both a KWW form and the same Prony series directly, the model will error out during the property check.

There are many useful optional parameters for the UPM model that generally allow for: temperature dependence of moduli, coefficients of thermal expansion, deformation dependence of moduli, and/or alternative material clock parameter specifications. These parameters may optionally be added to the material input block, but are defaulted to 0.0:

### OPTIONAL parameters for the universal_polymer model
 CLOCK C1         = <real> # CLOCK Coef. 1 instead of "WLF C1"
 CLOCK C2         = <real> # CLOCK Coef. 1 instead of "WLF C2"
 BULK GLASSY 1    = <real> # Pressure per Temperature
 BULK RUBBERY 1   = <real> # Pressure per Temperature
 SHEAR GLASSY 1   = <real> # Pressure per Temperature
 SHEAR RUBBERY 1  = <real> # Pressure per Temperature
 VOLCTE GLASSY 1  = <real> # Inverse Temperature Squared
 VOLCTE RUBBERY 1 = <real> # Inverse Temp. Squared

Finally, we note that the UPM model may be reduced to a finite deformation, linear thermoviscoelastic model by choosing \(C_3 = 0\) and \(C_4 = 0\). Under these conditions the material clock is only temperature (history) dependent but involves no deformation dependence. Moreover, if one wants to fix the laboratory and material time scales to be the same, then one should set WLF \(C_1\) = 0.

The Universal Polymer Model (UPM) is a phenomenological, non-linear viscoelastic (NLVE) model that is, in the literature, named the Simplified Potential Energy Clock (SPEC) [[44]]. The UPM model is considerably simpler than the parent model, the Potential Energy Clock (PEC) model, labeled the NLVE polymer model in SIERRA, which itself is not phenomenological but requires extensive data and experience to calibrate [[45]].

The UPM model is suitable for modeling the finite deformation, thermal-mechanical behavior of glassy materials, both organic and inorganic. Successful usage of the model is widespread. Some examples include the modeling of amorphous, thermosetting polymers across and through the glass transition such as epoxies [[46]]. It is also suitable for modeling thermoplastics from within the melt state and down into the glass transition from polystyrene to polycarbonate. Finally, it has been used to represent inorganic glasses for glass-to-metal seals. The UPM model was developed for production analyses of encapsulated components. It predicts a full range of behavior including yielding, stress relaxation, volume relaxation, and physical aging.

The key physical principal behind the UPM model is that there exists a material time scale (material clock) separate from the laboratory time scale. If the material time scale is fast, such as in the rubbery state of a polymer, then the UPM model responds instantly to changes in temperature and strain such that the user would observe rate-independent behavior. However, if the material clock is slow relative to the laboratory time scale, viscoelastic memory builds with any process, which causes acute history and thermodynamic path dependent behavior.

The model response is derived from a Helmholtz Free Energy density and takes as an input the unrotated rate of deformation, \(d_{ij}\), the temperature at the start and end of the time step \(\theta_{n}\) and \(\theta_{n+1}\), and the time step, \(\Delta\,t\). From these inputs, the hereditary integrals within the model are updated, and the unrotated Cauchy stress tensor is returned.

For the UPM model, the strain measure is approximated from the integrated unrotated rate of deformation tensor, which we label \(\epsilon_{ij}\),

\[\epsilon_{ij} = \int_{0}^{\infty} \left( R_{mi}D_{mn} R_{nj} \right) ds, \quad D_{ij} = \frac{1}{2}\left( L_{ij} + L_{ji}\right), \quad F_{ij} = R_{im} U_{mj}.\]

Here, \(F_{ij}\), \(R_{ij}\), \(U_{ij}\), \(L_{ij}\), and \(D_{ij}\) are the deformation gradient, rotation, material stretch, velocity gradient, and rate of deformation tensors standard in Lagrangian continuum mechanics.

The UPM model allows the user to initiate an analysis from a stress-free temperature, \(\theta_{\rm sf}\), that is different from the reference temperature, \(\theta_{\rm ref}\), at which all material properties are defined. Here we briefly summarize the constitutive equations. The model is derived from a Helmholtz Free Energy, but we begin directly with the (unrotated) Cauchy Stress and refer the reader to reference [[44]] for more detail:

(5.87)\[\begin{split}\sigma_{ij} = & \left( K_{G}\left( \theta \right) - K_{\infty} \left( \theta \right) \right) \int_{0}^{t}{f_v\left(t' - s'\right)}\frac{d I_1}{ds}{ds}\delta_{ij} \\ & - \left(K_{G}\left( \theta \right) \delta_{G}\left(\theta\right) - K_{\infty} \left(\theta\right)\delta_{\infty} \left(\theta\right) \right) \int_{0}^{t}{f_v\left( t' - s'\right)}\frac{d \theta}{ds}{ds}\delta_{ij} \nonumber \\ & +2 \left( G_{G}\left( \theta \right) - G_{\infty} \left(\theta \right) \right) \int_{0}^{t}{f_{s}\left(t' - s'\right)} \frac{d \left( {\rm dev} \epsilon_{ij} \right)}{ds} ds \nonumber \\ & + \left( K_{\infty} \left( \theta \right) I_1 - K_{\infty} \left( \theta \right) \delta_{\infty} \left( \theta \right) \left( \theta - \theta_{\rm sf} \right) \right) \delta_{ij} + 2 G_{\infty} \left( \theta \right) {\rm dev} \epsilon_{ij}. \nonumber\end{split}\]

The first three lines of terms in (5.87) represent the time-dependent and dissipative (non-equilibrium) response of the model to volumetric, thermal, and shear deformation histories. Accordingly, \(K\), \(\delta\), and \(G\) represent a bulk modulus, volumetric thermal expansion coefficient, and shear modulus while subscripts \(_G\) or \(_\infty\) denote a glassy or rubbery, respectively, properties. The last collection of terms in (5.87) furnish the time-independent rubbery (equilibrium) response. The variables in equation (5.87) are:

(5.88)\[\begin{split}I_1 & = \delta_{ij}\epsilon_{ij} = {\rm tr} \epsilon_{ij}, \qquad\qquad\quad {\rm dev}\epsilon_{ij} = \epsilon_{ij} - \frac{ I_1 }{3}\delta_{ij} , \\ G_G \left( \theta \right) & = G_G^{\rm ref} + \frac{dG_G}{d\theta} \left( \theta - \theta_{\rm ref}\right) , \quad G_\infty \left( \theta \right) = G_\infty^{\rm ref} + \frac{dG_\infty}{d\theta} \left( \theta - \theta_{\rm ref}\right) , \\ K_G \left( \theta \right) & = K_G^{\rm ref} + \frac{dK_G}{d\theta} \left( \theta - \theta_{\rm ref}\right) , \quad K_\infty \left( \theta \right) = K_\infty^{\rm ref} + \frac{dK_\infty}{d\theta} \left( \theta - \theta_{\rm ref}\right) , \\ \delta_G \left( \theta \right) & = \delta_G^{\rm ref} + \frac{ d \delta_G}{d\theta} \left( \theta - \theta_{\rm ref}\right) , \quad \delta_\infty \left( \theta \right) = \delta_\infty^{\rm ref} + \frac{ d \delta_\infty}{d\theta} \left( \theta - \theta_{\rm ref}\right).\end{split}\]

The first three terms in (5.87) represent the material’s viscoelastic response to changes in volume strain, temperature, and shear deformation. Two relaxation functions are used to characterize the thermal/volumetric (\(f_v\)) and shear (\(f_v\)) relaxation responses. The model assumes the thermal and volumetric relaxation responses are identical. Otherwise, \(f_v\) and \(f_s\) are typically quite different and are expressed as a Prony series footnote{Note: to distinguish between indices used with conventional summation convention and those related to Prony series terms, all Prony series summations shall be explicitly written with the relevant index given parenthetically in a superscript.}:

(5.89)\[f_v\left(x\right) = \sum_{k=1}^{N} w^{\left(k\right)} \exp \left( -\frac{x}{\tau^{\left(k\right)}} \right), \quad f_s\left(x\right) = \sum_{l=1}^{M} w^{\left(l\right)} \exp \left( -\frac{x}{\tau^{\left(l\right)}} \right).\]

These relaxation functions describe the material’s response to a suddenly applied volumetric/thermal or shear perturbation at the reference temperature where, under certain conditions, the material and laboratory time scales are equivalent. In (5.87), the viscous terms (non-rubbery) involve hereditary integrals over the difference in material time from \(s=0\) to \(s=t\), which is the current laboratory time.

An increment in material time, \(dt'\), and the laboratory time, \(dt\), are related through the (highly) history dependent shift factor, \(a\), such that the difference in material time, \(t' - s'\), is related to the corresponding difference in laboratory time, \(t - s\) through:

\[a dt' = dt, \quad t' - s' = \int_{u=s}^{u=t} \frac{du}{a\left(u\right)}.\]

If the material time scale is very slow compared to the laboratory time, then \(a>>1\), which is often the case inside and below the glass transition for typically glassy materials.

The shift factor is instantaneously defined through:

(5.90)\[\begin{split} {\rm log_{10}} a = & \frac{-C_1 N}{ C_2 + N }, \\ N(t) = &\theta - \theta_{\rm ref} - \int_0^t f_v\left( t' - s' \right) \frac{d\theta}{ds}ds \\ & + C_3 \left( I_1 - \int_0^t f_v\left( t' - s' \right) \frac{d I_1}{ds}ds \right) \nonumber \\ & + C_4 \int_{u=0}^{u=t} \int_{s=0}^{s=t} \left( f_{s}\left( t' - s' , t' - u' \right)\frac{d \left( {\rm dev}\epsilon_{ij} \right)}{ds}\frac{d \left( {\rm dev} \epsilon_{ij} \right)}{du} ds du \right).\nonumber\end{split}\]

The key physics in the model comes form (5.90). Temperature rise (generally) causes \(N\) to increase, and hence the material shift factor shrinks (the material time scale speeds up). Shrinking the volume generally causes the shift factor to increase as if the temperature had been decreased. Mechanistically, this feature is the manifestation of the trade-off between between mobility and free volume available to polymer chains. Finally, shear deformation can greatly speed up the material clock through the last term. This phenomenon is a direct manifestation of “deformation induced mobility”, a key mechanism for glassy materials.

Since the shift factor involves hereditary integrals, even at a constant temperature and state of deformation, the material clock will change over time. Under stress-free conditions, the material will creep and densify if the model is out of equilibrium (when any viscous term is non-zero). These phenomena are the model’s manifestations of physical aging, time-dependent material change without a change in composition or microstructure. \(C_1\), \(C_2\), \(C_3\), and \(C_4\) are all material constants. We note that the double relaxation function appearing in the last term takes on a slightly different form from \(f_s\):

(5.91)\[f_{s}\left( x, y \right) = \sum_{k=1}^{N} w^{\left(k\right)} \exp\left( -\frac{x}{\tau^{\left(k\right)}} \right) \exp\left( -\frac{y}{\tau^{\left(k\right)}} \right)\]

It is desirable to relate a special case of the model to the Williams-Landel-Ferry (WLF) form because of how time-temperature superposition fitting is typically performed. Specifically, one can show that the clock parameters, \(C_1\) and \(C_2\), relate to the WLF parameters, \(\hat{C}_1\) and \(\hat{C}_2\), through the following relationships: \(\hat{C}_1 = C_1\) and \(\hat{C}_2 = C_2 /\left(1 + C_3 \delta_{\infty}^{\rm ref} \right)\).

For more information about the universal polymer model, consult [[44]].

Output variables available for this model are listed in Table 5.28. The user should always output the shift factor \(aend\) or log:math:_{10}a as this variable is critical for interpreting the material behavior.

Table 5.28 State Variables for Universal Polymer Model

Name

Description

aend

The shift factor relating increments of material to laboratory time, \(a\, dt^* = dt_{\rm lab}\)

loga

\({\rm log_{10}}\) of the shift factor, \({\rm log_{10}}a\)

epsxx

xx component of the integrated unrotated rate of deformation, \(\epsilon_{xx}\)

epsyy

yy component of the integrated unrotated rate of deformation, \(\epsilon_{yy}\)

epszz

zz component of the integrated unrotated rate of deformation, \(\epsilon_{zz}\)

epsxy

xy component of the integrated unrotated rate of deformation, \(\epsilon_{xy}\)

epsyz

yz component of the integrated unrotated rate of deformation, \(\epsilon_{yz}\)

epszx

zx component of the integrated unrotated rate of deformation, \(\epsilon_{zx}\)

effi2

second (non-Cayley Hamilton) invariant of \(\epsilon\) providing shear deformation, \(I_2\)

if1p1-30

volumetric hereditary integrals 1-30

ikat1-30

thermal hereditary integrals 1-30

igxx1-30

xx component shear hereditary integrals 1-30

igyy1-30

yy component shear hereditary integrals 1-30

igzz1-30

zz component shear hereditary integrals 1-30

igxy1-30

xy component shear hereditary integrals 1-30

igyz1-30

yz component shear hereditary integrals 1-30

igzx1-30

zx component shear hereditary integrals 1-30

5.2.33. Mooney-Rivlin Model

BEGIN PARAMETERS FOR MODEL MOONEY_RIVLIN
  #
  # Elastic constants, One of these elastic constants must be input.
  # The shear modulus is computed from C10 and C01.
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  #
  #
  C10 = <real>c10
  C01 = <real>c01
  C10 FUNCTION = <string>c10_function_name
  C01 FUNCTION = <string>c01_function_name
  BULK FUNCTION = <string>bulk_function_name
  THERMAL EXPANSION FUNCTION = <string>eth_function_name
  TARGET E = <real>target_e
  TARGET E FUNCTION = <string>etar_function_name
  MAX POISSONS RATIO = <real>max_poissons_ratio(0.5)
  REFERENCE STRAIN = <real>reference_strain
END [PARAMETERS FOR MODEL MOONEY_RIVLIN]

Mooney-Rivlin is a hyperelastic material model that is used to describe rubber. The Mooney-Rivlin model incorporates temperature-dependent material moduli and can be used in both Presto and Adagio. When the model is used in Adagio, it can be used with or without the control-stiffness option in Adagio’s multilevel solver. The control-stiffness option is implemented via the CONTROL STIFFNESS command block and is discussed in Section 4. The model is used to simulate nearly incompressible materials where Poisson’s ratio, \(\nu\), \(\approx 0.5\). In the course of solving a series of model problems in Adagio, the material response from this model incorporates scaling the bulk and/or shear behaviors to yield a material response that is more amenable to solution using Adagio’s conjugate gradient solver. The final material behavior that is calculated corresponds to the actual moduli that are specified. When this model is used in Presto, the material scalings are ignored.

In the above command blocks the following command lines are required:

  • The material constants C10 and C01 determine the shear behavior as defined by

    (5.92)\[\texttt{shear\_modulus} = 2 \left(C_{10} + C_{01}\right).\]

    Thus the C10 and C01 command lines must be included in this model and the shear modulus elastic constant is not an available input.

  • Since C10 and C01 define the shear behavior, one additional elastic constant, other than the shear modulus is required to define the unscaled bulk behavior. See Section 5.1.5 for more information on elastic constants input.

Other command line options include:

  • The C10 FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes the temperature dependence of the C10 material parameter. This command line is optional. If it is not present, there is no temperature dependence in the C10 parameter. See the usage discussion below.

  • The C01 FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes the temperature dependence of the C01 material parameter. This command line is optional. If it is not present, there is no temperature dependence in the C01 parameter. See the usage discussion below.

  • The BULK FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes the temperature dependence of the bulk modulus. This command line is optional. If it is not present, there is no temperature dependence in the bulk modulus. See the usage discussion below.

  • The THERMAL EXPANSION FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes the linear thermal expansion as function of temperature. This command line is optional. If it is not present, there is no thermal expansion. See the usage discussion below.

  • The following material-scaling command lines are used only in Adagio:

    • The target Young’s modulus is defined with the TARGET E command line. This command line is optional. See the usage discussion below.

    • The TARGET E FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes the time variation of the target Young’s modulus. This command line is optional. If it is not present, there is no time dependence in the Target E parameter. See the usage discussion below.

    • The maximum Poisson’s ratio is defined with the MAX POISSONS RATIO command line. This command line is optional and will default to 0.5 if not specified. See the usage discussion below.

    • The reference strain is defined with the REFERENCE STRAIN command line. This command line is optional. See the usage discussion below.

The command lines for functions that specify the temperature dependence of C10, C01, and bulk modulus are optional, e.g., the C10 FUNCTION, C01 FUNCTION and BULK FUNCTION command lines. If these command lines are not included, their corresponding material parameters are taken to be independent of temperature. Mooney-Rivlin, like other material models, allows for the specification of thermal strain behavior within the material model itself, via the THERMAL EXPANSION FUNCTION command line. This command line, like the other “function-type” command lines in this model requires that a function associated with the name be defined in the SIERRA scope.

The bulk and shear scalings that can be used with the multilevel solver in Adagio are specified via a combination of the TARGET E, TARGET E FUNCTION, and MAX POISSONS RATIO command lines. If the TARGET E command line is not included (and the MAX POISSONS RATIO command line is included), the shear scaling is set to 1.0, and the bulk scaling is determined from the ratio of the scaled bulk modulus to its unscaled value, where the scaled bulk modulus is computed using the value of the max_poissons_ratio parameter along with the unscaled initial shear modulus that is determined from the value of the parameters specified in the C10 and C01 command lines. On the other hand, if both the TARGET E command line and the MAX POISSONS RATIO command line are included, bulk and shear scaling values are computed using scaled moduli that are calculated from the target_e and max_poissons_ratio parameter values.

Including the TARGET E FUNCTION command line allows time-dependent bulk and shear scaling to be used. If this command line is not specified, the bulk and shear scalings remain constant in solution time. If the command line is specified, the target Young’s modulus that is used for computing the scaled moduli is multiplied by the function value.

The REFERENCE STRAIN command line supplies a value for the reference strain used to create a normalized material constraint violation that is based on strains. Specifying a reference strain implies the use of strains for measuring the material constraint violation (or part of the control-stiffness error in Adagio). Otherwise, the material constraint violation is determined using the change in the scaled stress response over the current model problem.

Brief documentation on the theoretical basis for the Mooney-Rivlin model is given in [[47]].

State variables for this model are listed in Table Table 5.29.

Table 5.29 State Variables for MOONEY RIVLIN Model (Section 5.2.33)

Index

Name

Variable Description

1

C10

material constant

2

C01

material constant

3

K

temperature scaled bulk modulus

4

SFJTH

total volumetric strain

5

JTH

thermal volumetric strain

6

SFJTH_FLAG

thermal expansion flag (1 if thermally expanding)

7

WDEV

distortion strain energy

8

SHEAR MODULUS

temperature scaled shear modulus calculated from C10 and C01

5.2.34. Stiff Elastic

BEGIN PARAMETERS FOR MODEL STIFF_ELASTIC
  #
  # Elastic constants
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  SHEAR MODULUS  = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  TWO MU         = <real>
  #
  #
  #
  SCALE FACTOR = <real>scale_factor
  REFERENCE STRAIN = <real>reference_strain
END [PARAMETERS FOR MODEL STIFF_ELASTIC]

The stiff elastic model is a variation of the isotropic elastic model. The stiff elastic model can be used in both implicit and explicit analysis. However, model is primarily intended to be used with implicit solution in conjunction with the control-stiffness multilevel solver. The control-stiffness option is implemented via the CONTROL STIFFNESS command block and is discussed in Section 4. The stiff elastic model is used slowly ramp of the stiffness of a stiff material during control stiffness solution to generate a material response more amenable to solution using the implicit conjugate gradient solver. The ultimate material stiffness that is used in the final control stiffness iteration corresponds to the actual moduli that are specified. Essentially when used with control stiffness this model provides an series of predictions and corrections of increasingly stiff materials. It is easier to solve this series of prediction analyses than to directly solve the original poorly conditioned full stiffness analysis.

When this model is used in explicit analysis, or without the control stiffness solver, the material scalings are ignored.

In the above command blocks:

  • See Section 5.1.5 for more information on elastic constants input. These constants define the true material stiffness.

  • The scaled bulk and shear moduli are computed using a Young’s modulus scaled by the value given by the SCALE FACTOR line command. These are the scaled down moduli used at the start of the control stiffness iteration.

  • The REFERENCE STRAIN command line supplies a value for the reference strain used to create a normalized material constraint violation that is based on strains. Specifying a reference strain implies the use of strains for measuring the material constraint violation (or part of the control-stiffness error in Adagio). Otherwise, the material constraint violation is determined using the change in the scaled stress response over the current model problem. Specifying a smaller reference strain means the material constraint is enforced more accurately.

This material has no state variables.

5.2.35. Swanson Model

BEGIN PARAMETERS FOR MODEL SWANSON
  #
  # Elastic constants, the shear modulus is computed
  # from A1, P1, B1, Q1, C1, and R1.
  # One of these elastic constants must be input.
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  #
  #
  A1 = <real>a1
  P1 = <real>p1
  B1 = <real>b1
  Q1 = <real>q1
  C1 = <real>c1
  R1 = <real>r1
  CUT OFF STRAIN = <real>ecut
  THERMAL EXPANSION FUNCTION = <string>eth_function_name
  TARGET E = <real>target_e
  TARGET E FUNCTION = <string>etar_function_name
  MAX POISSONS RATIO = <real>max_poissons_ratio
  REFERENCE STRAIN = <real>reference_strain
END [PARAMETERS FOR MODEL SWANSON]

The Swanson material model is a hyperelastic constitutive model that is used to simulate rubber. The Swanson model can be used in both Presto and Adagio. When the model is used in Adagio, it can be used with or without the control-stiffness option in Adagio’s multilevel solver for nearly incompressible materials where Poisson’s ratio, \(\nu\), \(\approx 0.5\). The control-stiffness option is implemented via the CONTROL STIFFNESS command block and is discussed in Section 4. In the course of solving a series of model problems in Adagio, the material response from this model incorporates scaling the bulk and/or shear behaviors to yield a material response that is more amenable to solution using Adagio’s conjugate gradient solver. The final material behavior that is calculated corresponds to the actual moduli that are specified. When this model is used in Presto, the material scalings are ignored.

In the above command blocks the following command lines are required:

  • The A1 command line defines \(A_1\) in (5.93).

  • The P1 command line defines \(P_1\) in (5.93).

  • The B1 command line defines \(B_1\) in (5.93).

  • The Q1 command line defines \(Q_1\) in (5.93).

  • The C1 command line defines \(C_1\) in (5.93).

  • The R1 command line defines \(R_1\) in (5.93).

  • The small-strain value used for computing the initial shear modulus is defined with the CUT OFF STRAIN command line. This defines \(e_c\) in (5.94).

  • The above properties define the shear behavior. One additional elastic constant other than the shear modulus is required to define the unscaled bulk behavior. See Section 5.1.5 for more information on elastic constants input.

Other command lines include:

  • The THERMAL EXPANSION FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes the linear thermal expansion as a function of temperature. This command line is optional. If it is not present, there is no thermal expansion. See the usage discussion below.

  • The following material-scaling command lines are used only in Adagio:

    • The target Young’s modulus is defined with the TARGET E command line. This command line is optional. See the usage discussion below.

    • The TARGET E FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes the time variation of the target Young’s modulus. This command line is optional. If it is not present, there is no time dependence in the Target E parameter. See the usage discussion below.

    • The maximum Poisson’s ratio is defined with the MAX POISSONS RATIO command line. This command line is optional and will default to 0.5 if not specified. See the usage discussion below.

  • The reference strain is defined with the REFERENCE STRAIN command line. This command line is optional. See the usage discussion below.

The strain energy density for the Swanson model is given by

(5.93)\[\begin{split}U = \frac{3}{2} \frac{A_1}{P_1 + 1} \left( \frac{\bar{I}_1}{3} - 1\right)^{P_1+1} + \frac{3}{2} \frac{B_1}{Q_1 + 1} \left( \frac{\bar{I}_2}{3} - 1\right)^{Q_1+1} \nonumber + \frac{3}{2} \frac{C_1}{R_1 + 1} \left( \frac{\bar{I}_1}{3} - 1\right)^{R_1+1}& \\ + K \left( J_m \ln{(J_m)} - J_m + 1 \right),&\end{split}\]

where \(\bar{I}_1\) and \(\bar{I}_2\) are the first and second invariants of the left Cauchy-Green strain tensor \(\bar{\mathbf{B}}\) which excludes volume change and thermal strains, \(J_m\) is the mechanical only part of the volume change which excludes thermal strains, and \(K\) is the bulk modulus.

As noted previously, only one of the standard elastic constants are required to define the unscaled bulk behavior. Together, the values for parameters in the A1, P1, B1, Q1, C1, and R1 command lines define the unscaled shear behavior, so these command lines must be present. The initial unscaled shear modulus is determined from those parameter values along with the value of the parameter in the CUT OFF STRAIN command line via

(5.94)\[\texttt{shear\_modulus} = {A_1}\left({\frac{{e_c}^{2}}{3}}\right)^{P_1} + {B_1}\left({\frac{{e_c}^{2}}{3}}\right)^{Q_1} + {C_1}\left({\frac{{e_c}^{2}}{3}}\right)^{R_1}\]

The Swanson model, like a few of the material models, allows for the specification of thermal strain behavior within the material model itself, via the THERMAL EXPANSION FUNCTION command line. This command line, like the other “function-type” command lines in this model, requires that a function associated with the name be defined in the SIERRA scope.

The bulk and shear scalings that can be used with the multilevel solver in Adagio are specified via a combination of the TARGET E, TARGET E FUNCTION, and MAX POISSONS RATIO command lines. If the TARGET E command line is not included (and the MAX POISSONS RATIO command line is included), the shear scaling is set to 1.0, and the bulk scaling is determined from the ratio of the scaled bulk modulus to its unscaled value, where the scaled bulk modulus is computed using the value of the max_poissons_ratio parameter along with the unscaled shear modulus. On the other hand, if both the TARGET E command line and the MAX POISSONS RATIO are included, bulk and shear scaling values are computed using scaled moduli that are calculated from the target_e and max_poissons_ratio parameter values.

Including the TARGET E FUNCTION command line allows time-dependent bulk and shear scaling to be used. If this command line is not specified, the bulk and shear scalings remain constant in solution time. If the command line is specified, the target Young’s modulus that is used for computing the scaled moduli is multiplied by the function value.

The REFERENCE STRAIN command line supplies a value for the reference strain used to create a normalized material constraint violation that is based on strains. Specifying a reference strain implies the use of strains for measuring the material constraint violation (or part of the control-stiffness error in Adagio). Otherwise, the material constraint violation is determined using the change in the scaled stress response over the current model problem.

Output variables available for this model are listed in Table Table 5.30. Brief documentation on the theoretical basis for the Swanson model is given in [[47]].

Table 5.30 State Variables for SWANSON Model (Section 5.2.35)

Index

Variable Description

1

SFJTH

total volumetric strain

2

JTH

thermal volumetric strain

3

VMECHXX

mechanical left stretch xx component

4

VMECHYY

mechanical left stretch yy component

5

VMECHZZ

mechanical left stretch zz component

6

VMECHXY

mechanical left stretch xy component

7

VMECHYZ

mechanical left stretch yz component

8

VMECHZX

mechanical left stretch zx component

9

SFJTH_FLAG

thermal expansion flag (1 if thermally expanding)

10

WDEV

distortion strain energy

5.2.36. Viscoelastic Swanson Model

BEGIN PARAMETERS FOR MODEL VISCOELASTIC_SWANSON
  #
  # Elastic constants, note shear modulus is computed
  # from A1, P1, B1, Q1, C1, and R1.
  # One of these elastic constants must be input.
  #
  YOUNGS MODULUS = <real>
  POISSONS RATIO = <real>
  BULK MODULUS   = <real>
  LAMBDA         = <real>
  #
  #
  BULK FUNCTION <string>bulk_func
  A1 = <real>a1
  A1 FUNCTION <string>a1_func
  P1 = <real>p1
  P1 FUNCTION <string>p1_func
  B1 = <real>b1
  B1 FUNCTION <string>b1_func
  Q1 = <real>q1
  Q1 FUNCTION <string>q1_func
  C1 = <real>c1
  C1 FUNCTION <string>c1_func
  R1 = <real>r1
  R1 FUNCTION <string>r1_func
  CUT OFF STRAIN = <real>ecut
  THERMAL EXPANSION FUNCTION = <string>eth_function_name
  PRONY SHEAR INFINITY = <real>ginf
  PRONY SHEAR 1 = <real>g1
  PRONY SHEAR 2 = <real>g2
  PRONY SHEAR 3 = <real>g3
  PRONY SHEAR 4 = <real>g4
  PRONY SHEAR 5 = <real>g5
  PRONY SHEAR 6 = <real>g6
  PRONY SHEAR 7 = <real>g7
  PRONY SHEAR 8 = <real>g8
  PRONY SHEAR 9 = <real>g9
  PRONY SHEAR 10 = <real>g10
  SHEAR RELAX TIME 1 = <real>tau1
  SHEAR RELAX TIME 2 = <real>tau2
  SHEAR RELAX TIME 3 = <real>tau3
  SHEAR RELAX TIME 4 = <real>tau4
  SHEAR RELAX TIME 5 = <real>tau5
  SHEAR RELAX TIME 6 = <real>tau6
  SHEAR RELAX TIME 7 = <real>tau7
  SHEAR RELAX TIME 8 = <real>tau8
  SHEAR RELAX TIME 9 = <real>tau9
  SHEAR RELAX TIME 10 = <real>tau10
  WLF COEF C1 = <real>wlf_c1
  WLF COEF C2 = <real>wlf_c2
  WLF TREF = <real>wlf_tref
  NUMERICAL SHIFT FUNCTION = <string>ns_function_name
  TARGET E = <real>target_e
  TARGET E FUNCTION = <string>etar_function_name
  MAX POISSONS RATIO = <real>max_poissons_ratio(0.5)
  REFERENCE STRAIN = <real>reference_strain
  SHEAR MODULUS UPDATE PENALTY = <real>Sherwood
END [PARAMETERS FOR MODEL VISCOELASTIC_SWANSON]

The viscoelastic Swanson model is a finite strain viscoelastic model that has an initial elastic response that matches the Swanson material model. The bulk response is elastic, while the shear response is viscoelastic. This model is commonly employed in simulating the response of rubber materials. The viscoelastic Swanson model can be used in both Presto and Adagio. When the model is used in Adagio, it can be used with or without the control-stiffness option in Adagio’s multilevel solver for nearly incompressible materials where Poisson’s ratio, \(\nu\), \(\approx 0.5\). The control-stiffness option is implemented via the CONTROL STIFFNESS command block and is discussed in Section 4. By solving a series of model problems in Adagio, the material response from this model incorporates scaling the bulk and/or shear behaviors to yield a material response that is more amenable to solution using Adagio’s conjugate gradient solver. The final material behavior that is calculated corresponds to the actual moduli that are specified. When this model is used in Presto, the material scalings are ignored.

In the above command blocks the following command lines are required:

  • Material constants command lines A1, P1, B1, Q1, C1, R1.

  • The small-strain value used for computing the glassy shear modulus is defined with the CUT OFF STRAIN command line. This defines \(e_c\) in (5.95).

  • The above parameters define the unscaled shear modules as defined by (5.95). One other elastic constant needs to be included to define the unscaled bulk behavior. The other elastic constant cannot be the shear modulus. See Section 5.1.5 for more information on elastic constants input.

  • PRONY SHEAR INFINITY command line.

  • WLF COEF C1 command line.

  • WLF COEF C2 command line.

  • WLF TREF command line.

Other optional command lines are:

(5.95)\[\texttt{shear\_modulus} = {A_1}\left({\frac{{e_c}^{2}}{3}}\right)^{P_1} + 2{B_1}\left({\frac{{e_c}^{2}}{3}}\right)^{Q_1}\]

  • The temperature variation of material constants A1, P1, B1, Q1, C1, R1 may be defined with their respective functions A1 FUNCTION, P1 FUNCTION, B1 FUNCTION, Q1 FUNCTION, C1 FUNCTION, and R1 FUNCTION.

  • The temperature variation of the BULK MODULUS constant may be defined with the BULK FUNCTION command line.

  • The THERMAL EXPANSION FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes the linear thermal expansion as a function of temperature. This command line is optional. If it is not present, there is no thermal expansion. See the usage discussion below.

  • The normalized relaxation spectra coefficients are specified with the PRONY SHEAR I command lines, where the value of I varies sequentially from 1 to 10.

  • The normalized relaxation spectra time constants are specified with the SHEAR RELAX TIME I command lines, where the value of I varies sequentially from 1 to 10.

  • NUMERICAL SHIFT FUNCTION command line.

  • The following material-scaling command lines are used only in Adagio:

    • The target Young’s modulus is defined with the TARGET E command line. This command line is required. See the usage discussion below.

    • The TARGET E FUNCTION command line references the name of a function defined in a FUNCTION command line in the SIERRA scope that describes the time variation of the target Young’s modulus. This command line is optional. If it is not present, there is no time dependence in the Target E parameter. See the usage discussion below.

    • The maximum Poisson’s ratio is defined with the MAX POISSONS RATIO command line. This command line is optional and will default to 0.5 if not specified. See the usage discussion below.

  • The reference strain is defined with the REFERENCE STRAIN command line. This command line is required. See the usage discussion below.

As noted previously, only two of the elastic constants are required to define the unscaled bulk behavior. Together, the values for parameters in the A1, P1, B1, Q1, C1, and R1 command lines define the unscaled glassy shear behavior, so these command lines must be present. The unscaled glassy shear modulus is determined from those parameter values along with the value of the parameter in the CUT OFF STRAIN command line, so this command line is also required.

The viscoelastic Swanson model, like a few of the material models, allows for the specification of thermal strain behavior within the material model itself, via the THERMAL EXPANSION FUNCTION command line. This command line, like the other “function-type” command lines in this model requires that a function associated with the name be defined in the SIERRA scope.

The bulk and shear scalings that can be used with the multilevel solver in Adagio are specified via a combination of the TARGET E, TARGET E FUNCTION, and MAX POISSONS RATIO command lines. If the TARGET E command line is not included (and the MAX POISSONS RATIO command line is included), the shear scaling is set to 1.0, and the bulk scaling is determined from the ratio of the scaled bulk modulus to its unscaled value, where the scaled bulk modulus is computed using the value of the max_poissons_ratio parameter along with the unscaled shear modulus. On the other hand, if both the TARGET E command line and the MAX POISSONS RATIO command line are included, bulk and shear scaling values are computed using scaled moduli that are calculated from the target_e and max_poissons_ratio parameter values.

Including the TARGET E FUNCTION command line allows time-dependent bulk and shear scaling to be used. If this command line is not specified, the bulk and shear scalings remain constant in solution time. If the command line is specified, the target Young’s modulus that is used for computing the scaled moduli is multiplied by the function value.

The REFERENCE STRAIN command line supplies a value for the reference strain used to create a normalized material constraint violation that is based on strains. Specifying a reference strain implies the use of strains for measuring the material constraint violation (or part of the control-stiffness error in Adagio). Otherwise, the material constraint violation is determined using the change in the scaled stress response over the current model problem.

The SHEAR MODULUS UPDATE PENALTY Is associated with how the viscoelastic Swanson model interacts with control stiffness. This command is not recommended for use at this time.

Output variables available for this model are listed in Table Table 5.31. Brief documentation on the theoretical basis for the viscoelastic Swanson model is given in [[47], [48], [49], [50]].

Table 5.31 State Variables for VISCOELASTIC SWANSON Model (Section 5.2.36)

Index

Name

Variable Description

1

SFJTH

total volumetric strain

2

JTH

thermal volumetric strain

3

VMECHXX

mechanical left stretch xx

4

VMECHYY

mechanical left stretch yy

5

VMECHZZ

mechanical left stretch zz

6

VMECHXY

mechanical left stretch xy

7

VMECHYZ

mechanical left stretch yz

8

VMECHZX

mechanical left stretch zx

9

VSXXDEV1 - VSXXDEV10

viscoelastic deviatoric PK2 stress xx

10

VSYYDEV1 - VSYYDEV10

viscoelastic deviatoric PK2 stress yy

11

VSZZDEV1 - VSZZDEV10

viscoelastic deviatoric PK2 stress zz

12

VSXYDEV1 - VSXYDEV10

viscoelastic deviatoric PK2 stress xy

13

VSYZDEV1 - VSYZDEV10

viscoelastic deviatoric PK2 stress yz

14

VSZXDEV1 - VSZXDEV10

viscoelastic deviatoric PK2 stress zx

15

SOXXDEV

instantaneous deviatoric PK2 stress xx

16

SOYYDEV

instantaneous deviatoric PK2 stress yy

17

SOZZDEV

instantaneous deviatoric PK2 stress zz

18

SOXYDEV

instantaneous deviatoric PK2 stress xy

19

SOYZDEV

instantaneous deviatoric PK2 stress yz

20

SOZXDEV

instantaneous deviatoric PK2 stress zx

21

WLF_AAVG

average WLF shift factor

22

ANAVG

average shift factor

23

WDEV

distortion strain energy

5.2.37. Additional Material Models in Development

In addition to the material models documented here, many additional material models are documented in the Sierra/SM Capabilities in Development manual, including

  • BARLAT PLASTICITY

  • ELASTIC ORTHOTROPIC

  • ELASTIC ORTHOTROPIC FAIL

  • ELASTIC ORTHOTROPIC DAMAGE

  • ELASTIC ORTHOTROPIC SHELL

  • FOAM DAMAGE

  • HONEYCOMB

  • KARAGOZIAN AND CASE CONCRETE

  • KAYENTA

  • LINEAR ELASTIC

  • HOSFORD PLASTICITY

  • KARAFILLIS BOYCE PLASTICITY

  • NLVE 3D ORTHOTROPIC

  • PIEZO

  • SHAPE MEMORY ALLOY

  • THERMO EP POWER

  • THERMO EP POWER WELD

  • UNIVERSAL POLYMER

The models, while available for use in Sierra/SM, should be used with caution as they may not be fully verified or supported, and available documentation may not be at the production level. Models in development are periodically moved to production after they have been documented and tested.