4.4.7. Level Set/CDFEM

Level set methods can be used to model multiphase flow where an evolving free surface must be accounted for. This section goes over how to set up a level set equation within Aria, as well as setting up a diffuse interface or sharp interface (CDFEM) approach.

4.4.7.1. Level Set Equation and Interface Definition

Within the Aria region, an input deck must define a level set equation system.

BEGIN EQUATION SYSTEM LS
  .
  [SOLVER SETTINGS]
  EQ LEVEL_SET FOR LEVEL_SET ON BLOCK_1 USING Q1 WITH MASS ADV SUPG
  .
END EQUATION SYSTEM

In the above input block, [SOLVER SETTINGS] includes any information about the nonlinear solution strategy, such as the maximum nonlinear iteration, nonlinear solution strategy etc. For the example above, the MASS and ADV terms are included. Level Set goes over the terms and formulation of the level set equation. SUPG stabilization is also added; information about SUPG stabilization can be found in SUPG. In addition to defining the level set equation system, a LEVEL SET INTERFACE must be defined in the Aria region scope.

BEGIN LEVEL SET INTERFACE LS
  .
  DISTANCE VARIABLE = SOLUTION->LEVEL_SET
  PERFORM INITIAL REDISTANCE = FALSE
  REDISTANCE METHOD = CLOSEST_POINT
  .
END LEVEL SET INTERFACE

The above shows some of the basic commands needed to define an interface, such as the distance variable and some commands associated with redistancing. Refer to Level Set Interface for more details on available commands for setting up a level set interface.

4.4.7.2. Redistancing the Level Set Field

As mentioned in Level Set, the advection of the level set field in general does not preserve the signed distance property. The integration of Eq. (3.91) can result in the formation of sharp and shallow gradients in the level set field $\levelSet$ ; these sharp and shallow gradients may result in numerical difficulties while solving Eq. (3.91) and inappropriate widening of the interface, respectively. To correct this, redistancing of the level set field is periodically done throughout the simulation. It should be noted that redistancing occurs in pseudo time, and not physical time. Aria utilizes Sierra/Krino to support two methods of redistancing the level set field: CLOSEST_POINT and FAST_MARCHING method. The default is the CLOSEST_POINT method.

The FAST_MARCHING was originally developed by Sethian [35] to solve boundary value problems of the Eikonal equation:

(4.6) $\| \nabla t_{a}(\vector{x}) \| &= \frac{1}{\extSpeed} \;\;\text{for}\;\; \vector{x} \in V \\ t_{a}(\vector{x}) &= 0\;\;\text{for}\;\; \vector{x} \in \Gamma$

where $t_{a}$ is a time of arrival and $\extSpeed$ is an extension speed of the interface; this type of equation describes the evolution of a closed interface $\Gamma$ as a function of $t_{a}$ with speed $\extSpeed$ in the direction normal to $\Gamma$ . Eq. (4.6) can be manipulated to look like the condition posed by Eq. (3.89):

(4.7) $\| \nabla \levelSet \| = 1$

which can be solved via the FAST_MARCHING method. For a more detailed description of this method, users are referred to [35].

The CLOSEST_POINT method reconstructs a piecewise linear representation of the $\levelSet = 0$ interface through elements that have differing signs of $\levelSet$ . From this, facets representing the interface are constructed and each node $i$ in the mesh finds a minimum distance $D_{i}$ to this set.

(4.8) $\levelSet_{i}^{*} = \text{sign}(\levelSet_{i}^{0})D_{i}$

where $\levelSet_{i}^{0}$ is the level set function prior to redistancing and $\levelSet_{i}^{*}$ is the newly redistanced level set. Given a sufficient density of facets, this procedure yields good results and is fast and robust.

Both FAST_MARCHING and CLOSEST_POINT redistancing methods can potentially perturb the $\levelSet = 0$ interface resulting in a loss of mass. A volume constraint is enforced to ensure that the phase volume is conserved throughout the entire simulation. A global constant $\varepsilon_{\levelSet}$ is solved from the following:

(4.9) $\int\limits_\Vol H_{A}^{0}(\levelSet^{*} + \varepsilon_{\levelSet}) d\Vol = \int\limits_\Vol H_{A}^{0}(\levelSet^{0}) d\Vol$

Where the sharp Heaviside function $H_{A}^{0}$ (indicated by a $0$ superscript) is used to measure the volume of phase A. The final redistanced level set $\levelSet_{i}$ is then computed by:

(4.10) $\levelSet_{i} = \levelSet_{i}^{*} + \varepsilon_{\levelSet}$

The redistancing options can be specified in the Solution Control Transient block. An example of performing redistancing after 7 physical time steps is shown below:

Begin Transient The_Time_Block_1
  .
  Event LS_CONSERVED_REDISTANCE when "(CURRENT_STEP - LAST_LS_CONSERVED_REDISTANCE_STEP) >= 7"
  .
End

Where the LS in LS_CONSERVED_REDISTANCE uses the name of the BEGIN LEVEL SET INTERFACE LS block declared in Level Set Equation and Interface Definition. For the above example, LS_CONSERVED_REDISTANCE has been selected; this means that the initial volume measured in Eq. (4.9) is only measured once at the beginning of the simulation. For applications where mass of a particular phase is introduced into the simulation domain over time, the LS_CONSTRAINED_REDISTANCE event can be used, which measures the initial volume in Eq. (4.9) at the end of each physical time step before redistancing event occurs.

4.4.7.3. Diffuse Interface Approach

Within Aria, there are options for representing the interface as either diffuse or sharp. A diffuse interface, which is modeled with a smooth Heaviside function $\heaviSmooth$ , varies the phase transition region (and therefore, phase properties) smoothly but sharply over a finite thickness. This thickness is typically related to the minimum element size in the mesh. The smooth Heaviside is evaluated as:

(4.11) $\heaviSmooth \equiv \begin{cases} 0 & \;\; \text{if} \;\; \levelSet < -\heaviWidth\\ \frac{1}{2}\left[1 + \frac{\levelSet}{\heaviWidth} + \frac{1}{\pi}\text{sin}\left(\frac{\pi\levelSet}{\heaviWidth}\right)\right] & \;\; \text{if} \;\; |\levelSet| \leq \heaviWidth\\ 1 & \;\; \text{if} \;\; \levelSet > \heaviWidth \end{cases}$

Here, the parameter $\heaviWidth$ controls the thickness of the interface, and is typically 2-3 times the minimum element size in the mesh. It can be seen that this smooth transition region between phases occurs in regions where $|\levelSet| < \heaviWidth$ . An example of this plotted in 1D against a level set variable $\levelSet$ where the interface is shown in Fig. 4.25. A interface thickness of $\heaviWidth = 3\Delta x$ was chosen here, where $\Delta x$ is the mesh size; Fig. 4.25 correspondingly shows that there are about 6 nodes across the interface thickness.

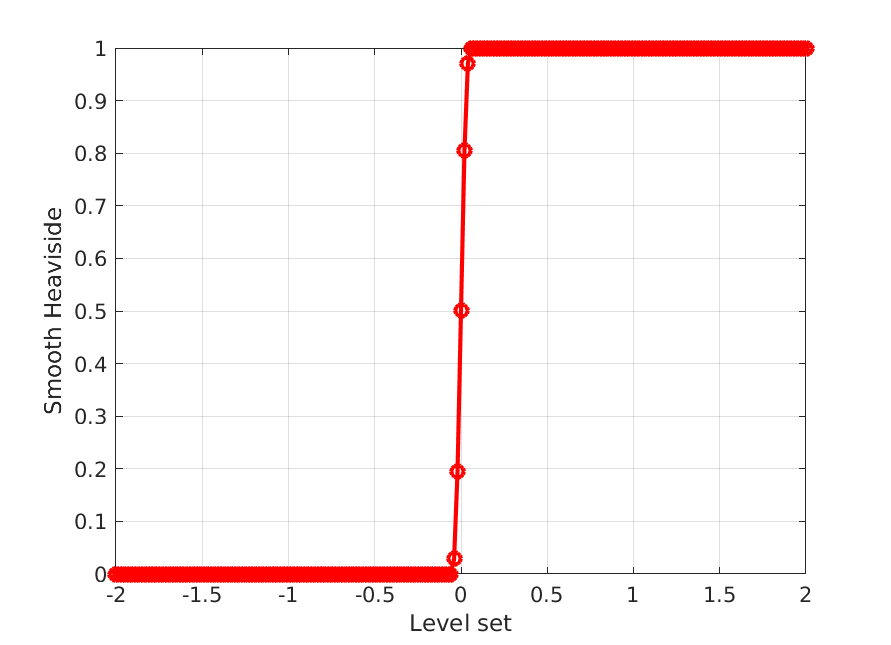
Schematic of 1D smooth Heaviside as a function of :math:`\levelSet` — Fig. 4.25 Schematic of 1D smooth Heaviside as a function of $\levelSet$ 

Fig. 4.25 Schematic of 1D smooth Heaviside as a function of $\levelSet$ 

To set up a diffuse interface modeling approach within Aria, at least 3 material blocks must be declared; one for each phase A and B (for a single level set), and one multiphase material that combines the two A and B materials:

BEGIN ARIA MATERIAL POS_MAT
  .
  DENSITY = CONSTANT rho = 1
  VISCOSITY = CONSTANT MU = 1.0e-5
  .
END ARIA MATERIAL POS_MAT
.
BEGIN ARIA MATERIAL NEG_MAT
  .
  DENSITY = CONSTANT rho = 1000.0
  VISCOSITY = CONSTANT MU = 1.0e-3
  .
END ARIA MATERIAL NEG_MAT
.
BEGIN ARIA MATERIAL MULTIPHASE
  .
  LEVEL SET HEAVISIDE = INTERPOLATED
  LEVEL SET WIDTH = CONSTANT width = 0.05
  DENSITY = PHASE_AVERAGE
  VISCOSITY = PHASE_AVERAGE
  SURFACE TENSION = CONSTANT sigma = 0.3
  MOMENTUM STRESS = INCOMPRESSIBLE_NEWTONIAN
  .
END ARIA MATERIAL MULTIPHASE

In the above input block, materials POS_MAT and NEG_MAT are declared for regions where $\levelSet$ are positive and negative, respectively. A third block, MULTIPHASE, is declared that defines the smooth Heaviside variable $\heaviSmooth$ with the LEVEL SET HEAVISIDE = INTERPOLATED command and the interface thickness $\heaviWidth$ with the LEVEL SET WIDTH command. Available options for these parameters can be found in Material Properties. It should be noted that in the above material definitions, a momentum stress model needs to be only defined for MULTIPHASE, and not POS_MAT or NEG_MAT. Lastly, material blocks are assigned within the FINITE ELEMENT MODEL scope. For a mesh that contains a block_1 that will be separated into phases by the level set field, the following is needed to define a diffuse interface:

BEGIN FINITE ELEMENT MODEL MYFEM
  BEGIN PARAMETERS FOR BLOCK BLOCK_1
    .
    MATERIAL MULTIPHASE
    PHASE A = POS_MAT
    PHASE B = NEG_MAT
    .
  END
END

4.4.7.4. Sharp Interface Approach with CDFEM

Aria offers the option to model the $\levelSet$ field as a sharp interface using Sierra/Krino. This is done through the conformal decomposition finite element method (CDFEM) developed by Noble et al. [36]. This is done by using the initial mesh as a background mesh, and cutting elements where the level set interfaces crosses into sub-elements to conform to the interface. The CDFEM approach to interface modeling will separate the original mesh into two distinct element blocks that represent each phase; the interface represented by the $\levelSet = 0$ contour is also represented as a distinct surface within the mesh, which can be used for any interfacial boundary applications.

To set up a simulation with CDFEM, a set of material blocks similar to the diffuse interface approach in Diffuse Interface Approach is declared:

BEGIN ARIA MATERIAL POS_MAT
  .
  DENSITY = CONSTANT rho = 1
  VISCOSITY = CONSTANT MU = 1.0e-5
  MOMENTUM STRESS = INCOMPRESSIBLE_NEWTONIAN
  .
END ARIA MATERIAL POS_MAT
.
BEGIN ARIA MATERIAL NEG_MAT
  .
  DENSITY = CONSTANT rho = 1000.0
  VISCOSITY = CONSTANT MU = 1.0e-3
  MOMENTUM STRESS = INCOMPRESSIBLE_NEWTONIAN
  .
END ARIA MATERIAL NEG_MAT
.
BEGIN ARIA MATERIAL POS_NEG_INTERFACE
  .
  SURFACE TENSION = CONSTANT SIGMA = 0.3
  .
END ARIA MATERIAL MULTIPHASE

In the above material blocks, the MOMENTUM STRESS model is defined for each individual phase; in addition the MULTIPHASE material block that was defined for the diffuse interface approach is removed. Instead, another material block POS_NEG_INTERFACE is defined, which will be the material block assigned to the surface block that represents the interface (which will be automatically generated by CDFEM).

Within the FINITE ELEMENT MODEL block, the following is defined for our example of a mesh with a single block block_1 that contains the level set interface:

BEGIN FINITE ELEMENT MODEL MYFEM
  BEGIN PARAMETERS FOR PHASE POS
    where LS is positive
  END
  .
  BEGIN PARAMETERS FOR PHASE NEG
    where LS is negative
  END
  .
  BEGIN PARAMETERS FOR BLOCK BLOCK_1_POS
    Material POS_MAT
  END
  .
  BEGIN PARAMETERS FOR BLOCK BLOCK_1_NEG
    Material NEG_MAT
  END
  .
  BEGIN PARAMETERS FOR SURFACE SURFACE_BLOCK_1_POS_NEG
    Material POS_NEG_INTERFACE
  END
END

The BEGIN PARAMETERS FOR PHASE command defines the individual block phases which are separated by the level set interface LS (defined in Level Set Equation and Interface Definition). From this, Sierra/Krino will create decomposed blocks based on these phase names: BLOCK_1_POS and BLOCK_1_NEG. These decomposed blocks must have materials assigned to them. Lastly, a surface that represents the $\levelSet = 0$ contour is created, which is named by combining the block name and their phases; in our example, this is SURFACE_BLOCK_1_POS_NEG. This surface requires a material block defining interfacial properties to be defined on it as well (POS_NEG_INTERFACE in our example). An example of this is shown in Fig. 4.26, where the original BLOCK_1 mesh is shown on the left (and is kept as a background mesh by CDFEM); the decomposed parts BLOCK_1_NEG and BLOCK_1_POS are shown on the right, which are separated by a the surface SURFACE_BLOCK_1_POS_NEG.

Schematic of an original ``BLOCK_1`` mesh decomposed into separate parts by CDFEM — Fig. 4.26 Schematic of an original `BLOCK_1` mesh decomposed into separate parts by CDFEM

In addition to defining a level set equation system on the original block (BLOCK_1), a similar set of equations must be assigned on the CDFEM-decomposed blocks as well:

EQ LEVEL_SET FOR LEVEL_SET ON BLOCK_1_NEG USING Q1 WITH MASS ADV SUPG
EQ LEVEL_SET FOR LEVEL_SET ON BLOCK_1_POS USING Q1 WITH MASS ADV SUPG

Surfaces that existed on the original mesh will also be decomposed in a similar manner. For our example, if there existed an original SURFACE_1, that surface will be decomposed into SURFACE_1_POS and SURFACE_1_NEG, which will correspond to the positive and negative phases, respectively.

A CDFEM OPTIONS block can be declared at the Aria region scope. An example of declaring a block like this is shown below:

BEGIN CDFEM OPTIONS
  .
  CDFEM EDGE TOLERANCE = 1.0e-2
  .
END

For a detailed list of CDFEM options and their purposes, refer to CDFEM Options.

4.4.7.5. Diffuse Level Set Approach to Modeling the Capillary Force

Aria offers various formulation for modeling the capillary (surface tension) force. The choice of the various capillary force implementations depend on the level set method used (diffuse or CDFEM); a result of this is that the momentum equation setup is also tailored to the selected level set approach. The following goes over setting up some of the basic implementations of the capillary forces; users should refer to the Command References for all available options.

To set up the momentum equation system, the following can be done (using the example from Diffuse Interface Approach):

EQ CONTINUITY_A FOR PRESSURE ON BLOCK_1 USING Q1 WITH DIV
EQ CONTINUITY_B FOR PRESSURE ON BLOCK_1 USING Q1 WITH DIV
EQ MOMENTUM_A FOR VELOCITY ON BLOCK_1 USING Q1 WITH DIFF ADV SRC SUPG
EQ MOMENTUM_B FOR VELOCITY ON BLOCK_1 USING Q1 WITH DIFF ADV SRC SUPG

The CONTINUITY and MOMENTUM equations are set up for both phases A and B. As mentioned in Diffuse Interface Approach, any discontinuities or jumps in the pressure or velocity field across phases A or B are smeared over the finite interface thickness.

In diffuse interface approaches, the surface tension force is represented as a continuous volumetric force, $\surfaceTensionBodyForce$ ; this is added as a source term to the momentum Eq. (3.23).

SOURCE FOR momentum ls A ON block_1 = LS_CAPILLARY
SOURCE FOR momentum ls B ON block_1 = LS_CAPILLARY

The LS_CAPILLARY source model is computed as (after taking a G/FEM residual form):

(4.12) $- \int\limits_\Vol \surfaceTensionBodyForce \bcdot\e_k\phi^i d\Vol$

With $\surfaceTensionBodyForce$ taking the form:

(4.13) $\surfaceTensionBodyForce = \surfaceTensionCoeff \levelSetCurv \levelSetNormal \dHeaviSmooth$

where $\surfaceTensionCoeff$ is a surface tension coefficient (which can be defined as a generic aria material property, refer to Material Properties for more details) and $\dHeaviSmooth$ is:

(4.14) $\dHeaviSmooth \equiv \begin{cases} 0 & \;\; \text{if} \;\; |\levelSet| > \heaviWidth\\ \frac{1}{2\heaviWidth}\left[1 + \text{cos}\left(\frac{\pi\levelSet}{\heaviWidth}\right)\right] & \;\; \text{if} \;\; |\levelSet| \leq \heaviWidth \end{cases}$

A similar model that can be implemented for diffuse interface is the LS_HEAVISIDE_CAPILLARY model, which converts the product of $\levelSetNormal \dHeaviSmooth$ in Eq. (4.13) into a Heaviside spatial gradient, $\nabla \heaviSmooth$ :

(4.15) $\surfaceTensionBodyForce = \surfaceTensionCoeff \levelSetCurv \nabla \heaviSmooth$

4.4.7.6. CDFEM Approach to Modeling the Capillary Force

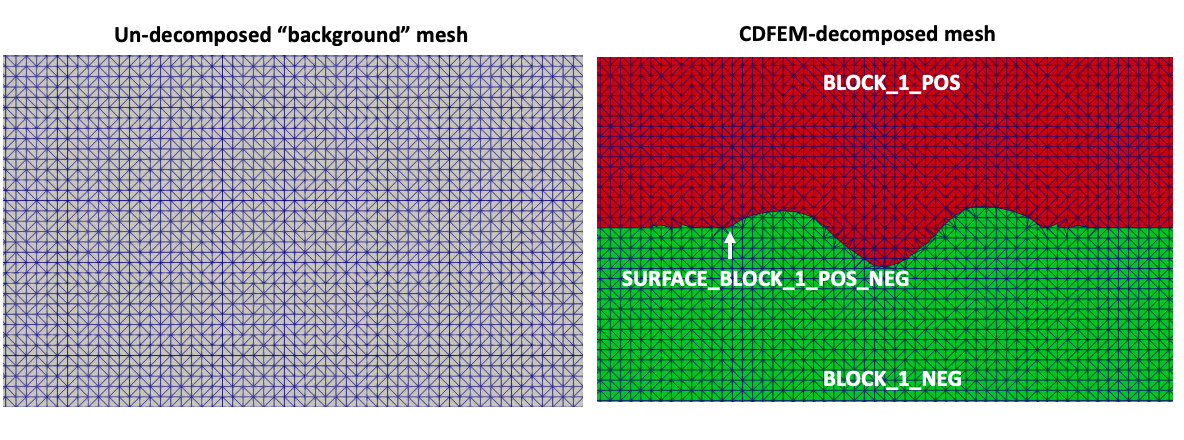
To set up the momentum equation system for a CDFEM approach requires a different format (using the example from Sharp Interface Approach with CDFEM, refer to Fig. 4.26 for a visual schematic):

EQ MOMENTUM FOR VELOCITY ON BLOCK_1_NEG USING Q1 WITH MASS ADV DIFF SRC SUPG
EQ MOMENTUM FOR VELOCITY ON BLOCK_1_POS USING Q1 WITH MASS ADV DIFF SRC SUPG
EQ CONTINUITY   FOR PRESSURE   ON BLOCK_1_NEG USING Q1 WITH DIV
EQ CONTINUITY_2 FOR PRESSURE_2 ON BLOCK_1_POS   USING Q1 WITH DIV

In the above command block, MOMENTUM equation systems are defined on both CDFEM-decomposed blocks BLOCK_1_POS and BLOCK_1_NEG. The CONTINUITY equation system is defined differently; there are 2 distinct pressure fields in the CDFEM domain (PRESSURE and PRESSURE_2). This is to capture the sharp discontinuity in the pressure field across the interface to balance the capillary force.

The approach for modeling capillary forces in CDFEM is different than a diffuse interface approach. This stems from the fact that we have a surface entity upon which we can enforce boundary conditions (fluxes) on; because of this, we are able to model the capillary forces as a boundary force $\surfaceTensionSurfaceForce$ across the interface instead of a volumetric smoothed force. This is enabled with the following command:

BC FLUX FOR MOMENTUM ON SURFACE_BLOCK_1_NEG_POS = CAPILLARY

It should be noted that CDFEM provides both SURFACE_BLOCK_1_NEG_POS and SURFACE_BLOCK_1_POS_NEG in our example; fluxes applied to these surfaces are applied to the NEG and POS phase/side of the level set interface, respectively. For the above command line, we are applying a capillary flux to the NEG phase/side. A G/FEM residual form of this is given as:

(4.16) $- \int\limits_\Surf \surfaceTensionSurfaceForce \bcdot\e_k\phi^i d\Surf$

For a BC FLUX approach for modeling capillary forces, $\surfaceTensionSurfaceForce$ is computed as:

(4.17) $\surfaceTensionSurfaceForce = \surfaceTensionCoeff \levelSetCurv \levelSetNormal$

Notice in Eq. (4.17) we no longer need $\dHeaviSmooth$ or $\nabla \heaviSmooth$ .

An alternative approach to modeling the capillary force is offered through the FLUXBP command (which stands for “flux by parts”). This models the capillary component to the MOMENTUM equation as a stress tensor $\surfaceTensionTensor$ as opposed to a surface force vector. The contribution to the G/FEM residual form becomes:

(4.18) $\int\limits_\Surf \surfaceTensionTensor :\grad\left(\e_k\phi^i\right) d\Surf$

The form of $\surfaceTensionTensor$ is similar to the form proposed by LaFaurie et al. ([37]), which takes a Laplace-Beltrami implementation of the capillary force:

(4.19) $\surfaceTensionTensor = \sigma \left(\identityTensor - \levelSetNormal \otimes \levelSetNormal \right)$

where $\identityTensor$ is the identity tensor. Notice that there is no curvature term $\levelSetCurv$ in Eq. (4.19) like there is in Eq. (4.17); this avoids the need to compute a second order derivative on the level set field $\levelSet$ . A detailed explanation of this $\surfaceTensionTensor$ term is given by Cairncross et al. [38].

An additional stabilization term $\surfaceTensionTensorStab$ can be added to Eq. (4.19) through the FLUXBP option. This acts to stabilize the capillary forces against larger time steps, and follows the form proposed by Hysing et al. ([39]):

(4.20) $\surfaceTensionTensorStab = -\viscosity \left(\levelSetNormal \cdot \nabla \v \right) \otimes \levelSetNormal$

where $\viscosity$ is the fluid viscosity. This term can be added in the input deck as

BC FLUX FOR MOMENTUM ON SURFACE_BLOCK_1_NEG_POS = CAPILLARY_STABILIZATION