I've worked on the following topics that have more of a computer-science or algorithmic flavor. All of this work is for distributed-memory parallel computers.
The RandomAccess benchmark as defined by the High Performance Computing Challenge (HPCC) tests the speed at which a machine can update the elements of a table spread across global system memory, as measured in billions (giga) of updates per second (GUPS). The parallel implementation provided by HPCC typically performs poorly on distributed-memory machines, due to updates requiring numerous small point-to-point messages between processors. We've developed an alternative algorithm whose computation (the GUP count) scales linearly with P while its communication overhead scales as log_2(P), thus enabling better performance on large numbers of processors. The new algorithm achieves a GUPS rate of 19.98 on 8192 processors of Sandia's Red Storm machine, compared to 1.02 for the HPCC-provided algorithm on 10350 processors.
After each processor generates a short list of table updates, it needs to send them to other processors. This communication can be formulated as a syncrhonous all2all operation. The key idea in our algorithm is to perform the all2all with a minimum number of large messages rather than the typical MPI implementation, which for the RandomAccess benchmark, would send large numbers of tiny messages.
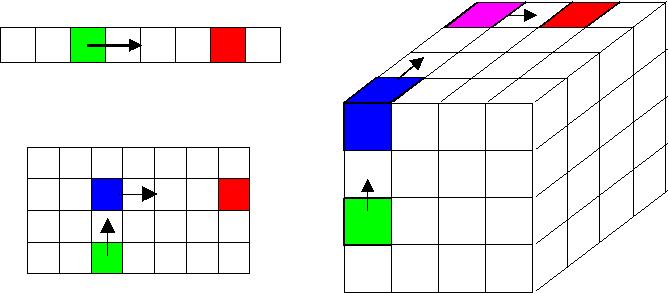
The basic idea is captured in this figure:

If P processors are viewed as a 1d list, the operation is a traditional all2all. In a single stage, each processor sends a message to (potentially) every other processor. The green processor sends data directly to the red processor. If the P processors are viewed logically as a 2d array, the operation can be performed in 2 stages. Each processor first communicates within its column, then within its row. To send a message from the green processor to red, green first sends to the blue processor and blue then sends to red. Similarly, for a 3d logical grid of processors, the all2all operation can be completed in 3 stages, green to blue to purple to red, with a further reduction in the number of messages. We believe this 3d diagram is the basic idea behind IBM's optimized implementation of the RandomAccess benchmark for their BG/L machine (3d torus) which has achieved 35.5 GUPS on 128K processors.
Note that moving to higher dimensions affords a large savings in the number of messages each processor sends. If P = 10000, then in 1d each processor sends 10000 messages to complete the all2all, but in 2d for a 100x100 logical array, each processor sends only 200 messages. The asymptotic limit of the figure is to view the processors as an N-dimensional hypercube (P = 2^N) and perform the all2all in N = log_2(P) stages, which is what our algorithm does. Thus, we minimize the number of messages that are sent, at the cost of resending each datum N times. For the GUPS problem, this can be a big win, since the message sizes are so small. In the large P limit, a machine's GUPS performance will nearly double with this algorithm each time that P is doubled, so long as the machine's communication network can support the message bandwidth required by each of the N stages of the all2all operation.
Here is a table of GUPS performance on Sandia's Red Storm (Cray XT3) machine. This is for the vanilla version of the code. With some MPI tuning and other optimizations, the hi-water mark was 19.98 on 8192 procs. You can see the non-power-of-2 version doesn't do quite as well as the power-of-2 version.
| Processors | 1 | 4 | 16 | 64 | 200 | 256 | 300 | 1024 | 4096 | 8192 | 10240 |
| GUPS (HPCC version) | 0.0147 | --- | 0.0105 | 0.0634 | --- | --- | --- | 0.195 | --- | 0.797 | --- |
| GUPS (new algorithm) | 0.0180 | 0.0377 | 0.0930 | 0.273 | 0.567 | 0.858 | 0.739 | 2.81 | 9.25 | 17.24 | 19.72 |
| Parallel Efficiency (%) | 100 | 52.4 | 32.3 | 23.7 | 15.8 | 18.6 | 13.7 | 15.2 | 12.5 | 11.7 | 10.7 |
A tar file you can download with source code for our algorithm is available from this page. Three simple stand alone codes are provided (power-of-2 and non-power-of-2) as well as modules that can be plugged directly into the HPCC harness to perform an official benchmark test.
Details of the algorithm and performance results are given in this paper:
A Simple Synchronous Distributed-Memory Algorithm for the HPCC RandomAccess Benchmark, S. J. Plimpton, R. Brightwell, C. Vaughan, K. Underwood, M. Davis, Proc of Cluster 2006 - IEEE International Conf on Cluster Computing, Sept 2006. (abstract)
Collaborators on this project:
My latest FFT work is distributed in the fftMPI library.
It supercedes an earlier package I worked on in the late 1990s, based on similar principles, which we just called a parallel FFT library and distributed freely.
Our original motivation for developing parallel FFTs is that we use complex-to-complex FFTs in several of our parallel codes. 2-d FFTs are used for synthetic aperture radar image processing. 3-d FFTs are used in our molecular dynamics code LAMMPS for computing long-range Coulombic effects via the particle-mesh Ewald method, and in density-functional electronic structure codes for alternating between real-space and reciprocal-space operator representations.
Multi-dimensional FFTs are typically computed as a series of 1-d FFTs. For example a 2-d FFT operates on a 2-d matrix where 1-d FFTs are first performed on each row of the matrix, then 1-d FFTs are performed down each column. If the data set is distributed across processors of a parallel machine, each processor can use fast library routines to compute on-processor 1-d FFTs for the subset of rows or columns it owns. This means the only issue for a parallel implementation is "transposing" or remapping the data set to get each dimension wholly on-processor when needed. For example, we do a 3-d parallel FFT as follows: remap the data (if needed) to get the x-dimension wholly on-processor, perform 1-d FFTs along the x-dimension, remap to get the y-dimension on- processor, perform 1-d FFTs in y, remap to get the z-dimension on-processor, perform 1-d FFTs in z, remap (if needed) to transform the data to the desired output layout.
One useful feature used by our applications, in both the newer fftMPI library and the older Parallel FFT Package, is that the libraries allow for very general styles of data layout across processors both on input to the routines as well as on output. The parallel algorithms perform serial 1d FFTs by either calling vendor-supplied library routines (e.g. Intel MKL) or the freely available FFTW library.
Rendezvous algorithms are a generalized way to perform communication on distributed-memory machines when processors do not know who to send their data to, nor which processors will be sending them data.
This paper describes rendezvous algorithms and gives several examples of their utility in large-scale particle-based simulation codes:
Rendezvous algorithms for large-scale modeling and simulation, S. J. Plimpton and C. Knight, J Parallel and Distributed Computing, 147, 184-195 (2021). (abstract)
An application of rendezvous algorithms in grid-based simulation codes is for computational procedures which employ multiple grids on which solutions are computed. For example, in multi-physics simulations a primary grid may be used to compute mechanical deformation of an object while a secondary grid is used for thermal conduction calculations. We illustrate such a case with these 2-d quad-element grids of a plate with 2 holes. The 1st grid might be optimal for a calculation of stress centered on the small hole. The 2nd grid might be optimal for thermal effects due to heating around the large hole.
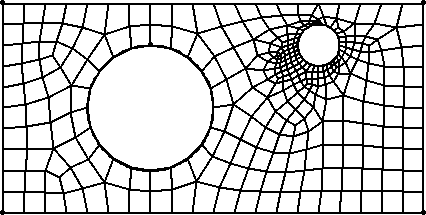

If one code is modeling both effects in a coupled fashion, solution data must be interpolated back and forth between the grids each timestep. On a parallel machine, this grid transfer operation can be challenging if the two grids are decomposed to processors differently for reasons of computational efficiency. If the grids move or adapt separately, the complexity of the operation is compounded.
We developed a grid transfer algorithm suitable for massively parallel codes which use multiple grids. It uses a rendezvous technique wherein a third decomposition is used to search for elements in one grid that contain nodal points of the other. This has the advantage of enabling the grid transfer operation to be load-balanced separately from the remainder of the computations.
This work was motivated by a multi-physics simulation framework effort at Sandia know as the Sierra project. Details of the grid transfer algorithm and some performance results are given in this paper:
A Parallel Rendezvous Algorithm for Interpolation Between Multiple Grids, S. J. Plimpton, B. Hendrickson, J. Stewart, J Parallel and Distributed Computing, 64, 266-276 (2004). (abstract)
Collaborators on this project:
For parallel computers, load-balancing is the assignment of work to processors in such a way that the computational load is evenly balanced. If this is done well, the code's parallel performance is typically maximized. In some applications, a one-time assignment of work can be pre-computed before the calculation begins and will be sufficient to maintain balance for the duration of the simulation. This is a "static" load-balancing approach. In other applications, work must be periodically redistributed among processors as the computation proceeds to maintain load-balance. These applications require some form of "dynamic" load balance, which is a much harder problem. My collaborator Bruce Hendrickson has written extensively on both static and dynamic balancing techniques.
With Pedro Diniz, a UC Santa Barbara student, we implemented and experimented with several dynamic algorithms in this conference paper:
Parallel Algorithms for Dynamically Partitioning Unstructured Grids, P. Diniz, S. J. Plimpton, B. Hendrickson, R. Leland, in Proc of 7th SIAM Conference on Parallel Processing for Scientific Computing, San Francisco, CA, February 1995, p 615. (abstract)
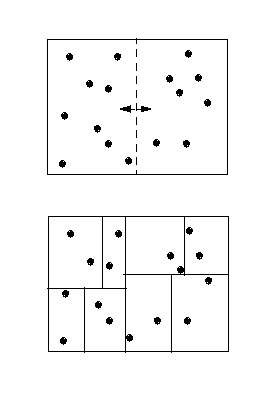
More recently, Sandia has developed a dynamic load-balancing library, called Zoltan, which has on-line documentation and is freely available to interested users. Some of my stuff has made its way into Zoltan. One example is a parallel implementation of the recursive coordinate bisectioning (RCB) technique which is a geometric-based partitioning method. A schematic is shown below of how RCB does parallel median searches to successively find planes (lines in 2-d) that split the domain in half; the result is a a set of small boxes (typically one per processor) that contain equal numbers of objects. The RCB operation is our method-of-choice anytime we need a fast geometric partitioner -- we've used it to good effect in PRONTO and our grid-transfer work.
Zoltan also includes a toolkit to assist the application in redistributing data once a re-balance has been performed. The communication operations in this toolkit are based on some irregular communication routines that Bruce and I wrote to enable processors to efficiently send data to other processors who don't know they'll be receiving the data. These algorithms have turned out to be quite useful in a variety of unexpected settings, such as the particle-in- cell code QuickSilver, the finite element NIMROD code for tokamak simulations, as well as in the aforementioned PRONTO and grid-transfer work.
My collaborator Bruce Hendrickson coined the term "tinkertoy" to describe our philosophy of parallel algorithm design. The idea lies somewhere between an overarching "frameworks" approach that many applications have adopted (e.g. PETSc or Sierra) and the simple interfaces provided by conventional numerical libraries (e.g. BLAS, LAPACK). The goal is to encapsulate basic functionality for parallel operations such as load-balancing or data-sharing between processors in such a way that routines can be easily hooked together in a variety of interesting modes. As our software and our thinking about tinkertoy modularity has evolved, the concept has enabled us to produce some sophisticated parallel algorithms with a minimum of new code development. For those who are object-orientation (OO) fans, we don't develop in C++, just plain-old C. Rather than use OO languages, we try to use OO design principles for encapsulation of data structures and interface functionality.
Projects that Bruce and I have worked on together based on the tinkertoy philosophy include the contact detection algorithms for PRONTO, grid_transfer, dynamic load balancing, and the communication operations in QuickSilver.
This paper describes the "tinkertoy" idea and outlines how several different applications can be architected from basic primitives:
Tinkertoy Parallel Programming: Complicated Applications from Simple Tools, B. Hendrickson and S. J. Plimpton, in Proc of SIAM Parallel Processing for Scientific Computing Conf, March 2001. (abstract)
Collaborators on this project:
The force-decomposition algorithm we developed for short-range molecular dynamics simulations turns out to have an analog in matrix-vector multiplies that are the kernel operation in iterative solvers. The same 2-d sub-blocking and row-wise and column-wise communication operations that we use for molecular dynamics can be effective for matrices whose structure cannot otherwise be exploited to produce a good parallel decomposition. The idea is described in this paper:
Parallel Many-Body Simulations Without All-to-All Communication, B. A. Hendrickson and S. J. Plimpton, J Parallel and Distributed Computing, 27, 15-25 (1995). (abstract)
The application of the force-decomposition idea to general many-body calculations (molecular dynamics or otherwise) is discussed in this paper:
An Efficient Parallel Algorithm for Matrix-Vector Multiplication, B. A. Hendrickson, R. W. Leland, S. J. Plimpton, Int J of High Speed Computing, 7, 73-88 (1995). (abstract)
Collaborators on this project: