12.2. Nonlocal Partitioning
Because communication in parallel processing scales with the surface area of the domain, we believed that software designed with the intent of limiting communication would be ideal for application to nonlocal regularization. Hence, graph-based (METIS, Zoltan Hypergraph) and geometric (Zoltan Recursive Coordinate Bisection, Zoltan Recursive Inertial Bisection) decomposition algorithms were implemented and available for the analyst. Fig. 12.1 illustrates the Zoltan partitioning methodologies for a circular region surrounding a sharp crack tip. We note that non-contiguous domains can occur in graph-based methodologies. For these reasons, ZOLTAN_RCB was selected to be the default partitioning scheme.
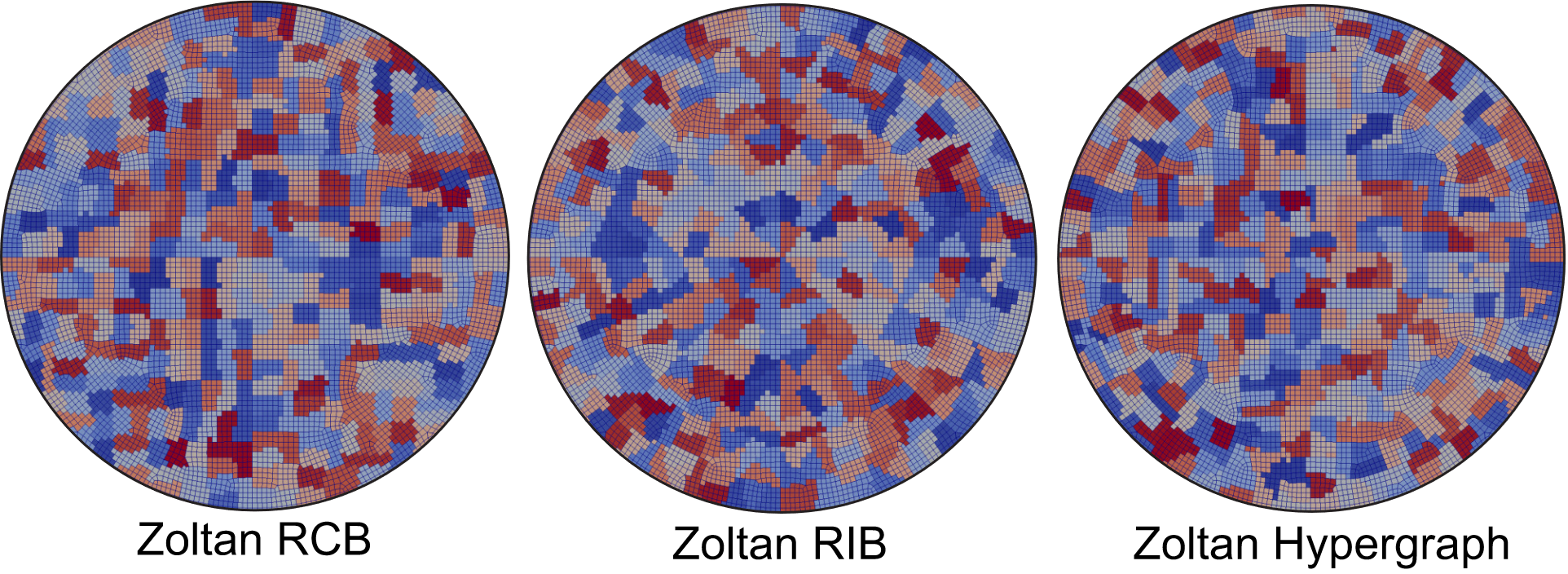
Fig. 12.1 Illustration of 400 nonlocal partitions at a sharp crack tip using Zoltan Recursive Coordinate Bisection (RCB), Zoltan Recursive Inertial Bisection (RIB), and Zoltan Hypergraph partitioning methodologies. Note that Zoltan Hypergraph can generate non-contiguous domains. The default partitioning methodology in Sierra is Zoltan RCB.
Initial findings employing geometric partitioning illustrated a sensitivity to domain shape. A re-examination of Fig. 12.1 will reveal that the aspect ratios of the domains are significant. Because we are aligning the evolution of a nonlocal variable with the nonlocal domain shape, domains of increasing aspect ratio result in anisotropic evolution. Although other researchers have developed methods for domain decomposition that focus on domain shape [[1]], we gravitated towards clustering algorithms and the resulting isotropy [[2]]. Fig. 12.2 illustrates the mesh, grid, and result of k-means clustering, a centroid Voronoi Tessellation (CVT). Given a body on processor with mesh size \(h\), we overlay a grid with uniform cell size \(c\). We then find points both inside (red) and outside (blue) the body. After calculating the number of nonlocal volumes \(N\) for a body of volume \(B\) through \(N = B/l^{3}\), we seed the centroids of the nonlocal domains through Zoltan RCB. K-means clustering of points inside the body evolves the locations of the centroids via Lloyd’s algorithm. The algorithm will converge to a CVT, independent of the FE discretization. The tolerance for convergence \(tol\) is specified as a fraction of the cell size \(c\). The nonlocal domains are then populated by each element’s proximity to the nearest CVT centroid. The resulting nonlocal domains are illustrated in Fig. 12.2. We note that the nonlocal domain size is only illustrative. Nonlocality in damage, for example, would require a smaller length scale \(l\) resulting in a finer discretization of Voronoi polygons.
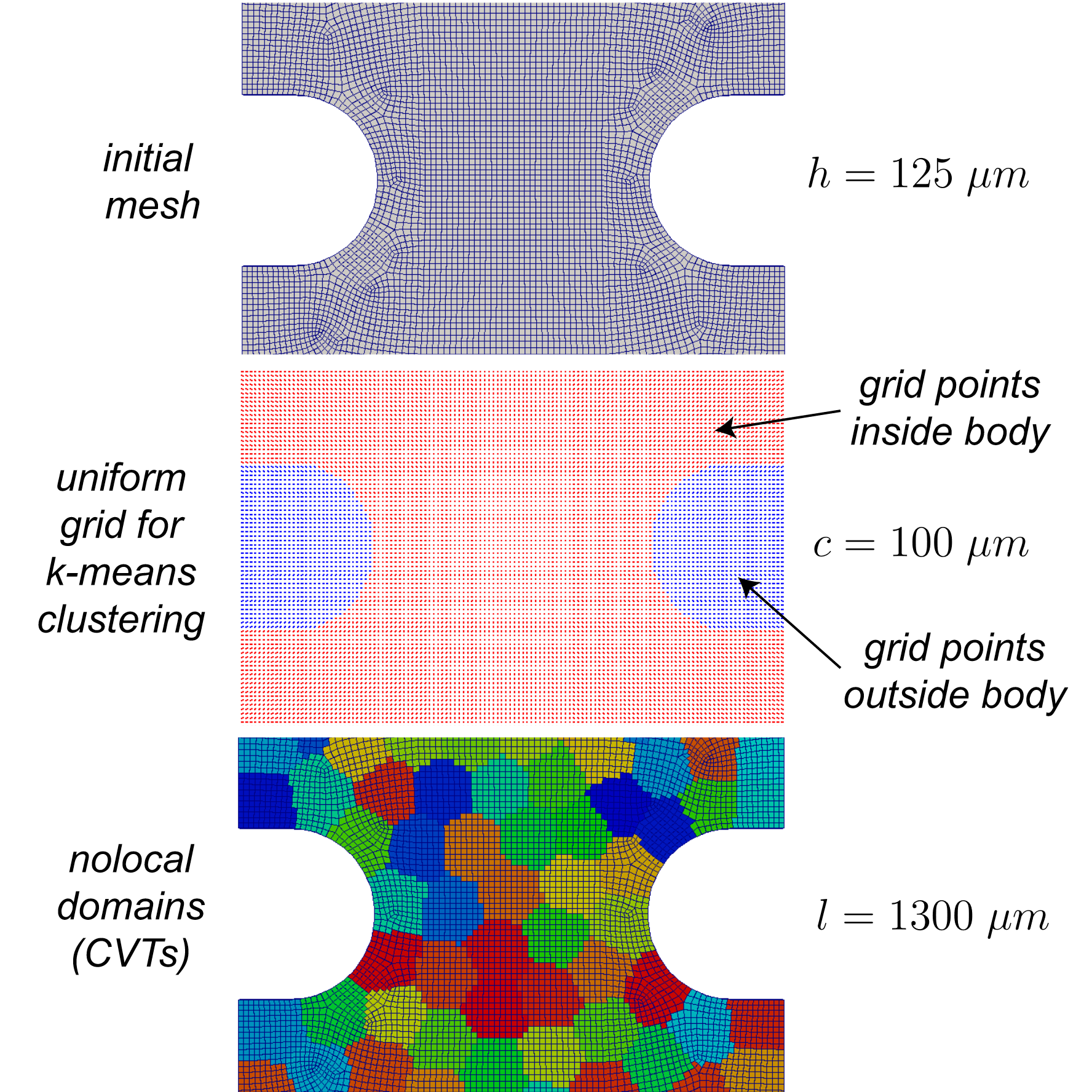
Fig. 12.2 Nonlocal domains derive from a Centroidal Voronoi Tessellation (CVT). A partitioned mesh for parallel processing with element size \(h\) determines the boundaries of a uniform grid with cell size \(c\). K-means clustering evolves a set of \(N\) centroids into a CVT.