16.2. Extrinsic Models

16.2.1. Tvergaard Hutchinson

This model is an extension of the trapezoidal traction-separation model proposed by Tvergaard and Hutchinson [[1]] generalized to multiple dimensions. The generalization is performed by appropriately scaling the normal and tangential components of the traction and separation into the 1D model depicted in Fig. 16.1. In Fig. 16.1, \(\lambda_c\) is the normalized final cohesive opening in the effective space, \(\lambda_1\) is the length of the initial loading branch of the model, \(\lambda_2\) is the separation length that begins the failure branch of the model, and \(\hat{\sigma}\) is the maximum effective traction of the cohesive zone. These parameters have the following restrictions on their values:

\[0 \leq \lambda_1 \leq \lambda_2 \leq \lambda_c = 1,\quad \hat{\sigma} > 0.\]

Finally, as shown in Fig. 16.1, for \(\lambda > \lambda_1\) unloading may be assumed towards the origin.

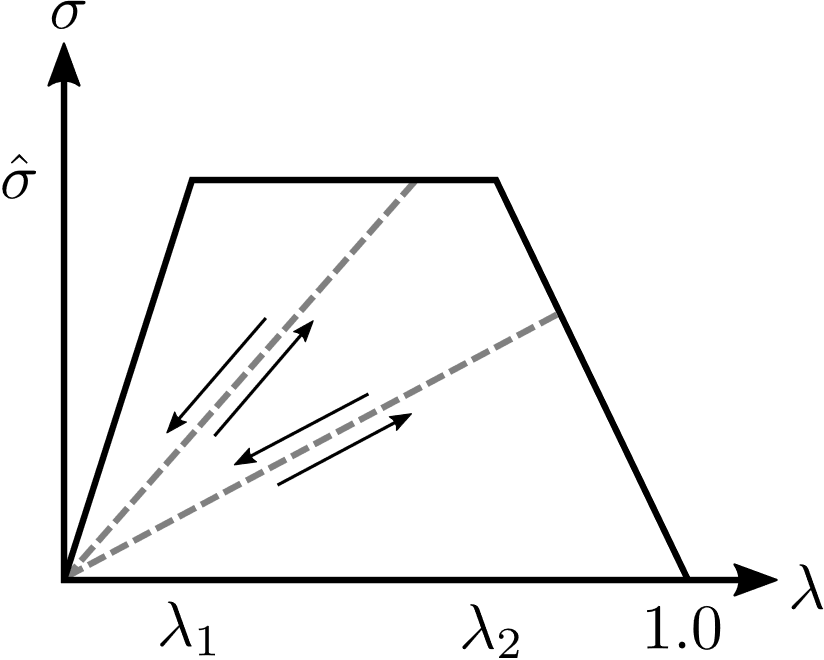
../../_images/tvergaard-hutchinson.png — Fig. 16.1 The effective traction-separation model following Tvergaard and Hutchinson.

Assuming a loading condition (\(\lambda > 0,\; \dot{\lambda} > 0\)), the slope of the effective traction-separation model is evaluated as follows

\[\begin{split}\hat{t}^{\prime} = \begin{cases} \hat{\sigma} / \lambda_1 , & \lambda \in [0,\,\lambda_1)\\ \hat{\sigma} / \lambda, & \lambda \in [\lambda_1, \lambda_2)\\ \hat{\sigma}(1-\lambda)/(\lambda(1-\lambda_2)), & \lambda \in [\lambda_2, \lambda_c)\\ 0, & \lambda \geq \lambda_c \end{cases}\end{split}\]

and the effective traction is computed as \(\hat{t} = \hat{t}^{\prime} \lambda\).

The effective traction-separation model is extended to 3D by defining the following additional values:

The normal failure separation, \(\delta_{cn}\)
The tangential failure separation, \(\delta_{ct}\)
The ratio of failure separations, \(r = \delta_{cn} / \delta_{ct}\)
The normalized normal separation, \(\lambda_n = u_n / \delta_{cn}\)
The normalized tangential separations, \(\lambda_t^i = u_t^i / \delta_{ct}\), \(i=1,\,2\).
The effective separation, \(\lambda = \sqrt{\lambda_n^2 + (\lambda_t^1)^2 + (\lambda_t^2)^2}\)

Then, the traction is computed as

\[\begin{split}t_t^1 =& \hat{t}^{\prime} \lambda_t^1 r,\\ t_t^2 =& \hat{t}^{\prime} \lambda_t^2 r,\\ t_n =& \hat{t}^{\prime} \lambda_n.\end{split}\]

The model is extended to the extrinsic behavior by computing an effective opening \(\tilde{\boldsymbol{\lambda}}\) that recovers the initialization traction. There are two modes of initialization: (1) where the initial effective traction is below the peak traction specified in the input file, and (2) where the initial effective traction exceeds the peak traction in the input file. In the first case, the components of the effective opening (\(\tilde{\boldsymbol{\lambda}}\)) are computed on the hardening branch of the cohesive model. In the second case, the peak traction is reset to the initial effective traction and the components of the initial effective opening are computed using the condition \(|\tilde{\boldsymbol{\lambda}}| = \lambda_1\). Evaluation of the extrinsic effective opening is given by the following:

\[\begin{split}\tilde{\sigma} =& \sqrt{(t_n r)^2 + (t_t^1)^2 + (t_t^2)^2}, \\ \hat{\sigma} =& \max(\hat{\sigma}, \tilde{\sigma}), \\ \tilde{\lambda}_t^i =& \frac{t_t^i \lambda_1}{\hat{\sigma} r},\; i=1,\,2, \\ \tilde{\lambda}_n =& \frac{t_n \lambda_n}{\hat{\sigma}}.\end{split}\]

After initialization, the model is evaluated using

\[\lambda = \sqrt{(\lambda_n + \tilde{\lambda}_n)^2 + (\lambda_t^1 + \tilde{\lambda}_t^1)^2 + (\lambda_t^2 + \tilde{\lambda}_t^2)^2}.\]

The model is specified in adagio by the following command block:

BEGIN PARAMETERS FOR MODEL TVERGAARD_HUTCHINSON
  INIT TRACTION METHOD = {IGNORE|ADD|EXTRINSIC} (IGNORE)
  LAMBDA_1 = <real>
  LAMBDA_2 = <real>
  NORMAL LENGTH SCALE = <real>
  TANGENTIAL LENGTH SCALE = <real>
  PEAK TRACTION = <real>
  PENETRATION STIFFNESS MULTIPLIER = <real>
  USE ELASTIC UNLOADING = {NO|YES} (YES)
END [PARAMETERS FOR MODEL TVERGAARD_HUTCHINSON]

The INIT TRACTION METHOD = EXTRINSIC|ADD command line relates only to the dynamic insertion of cohesive zone elements through element death or XFEM.

16.2.2. Thouless Parmigiani

This model is an extension of the Tvergaard Hutchinson effective traction-separation model described in Section 16.2.1, but the normal and tangential traction components are treated independently. The model is specified in adagio by the following command block:

BEGIN PARAMETERS FOR MODEL THOULESS_PARMIGIANI
  INIT TRACTION METHOD = {IGNORE|ADD|EXTRINSIC} (IGNORE)
  LAMBDA_1_N = <real>
  LAMBDA_1_T = <real>
  LAMBDA_2_N = <real>
  LAMBDA_2_T = <real>
  NORMAL LENGTH SCALE = <real>
  PEAK NORMAL TRACTION = <real>
  TANGENTIAL LENGTH SCALE = <real>
  PEAK TANGENTIAL TRACTION = <real>
  PENETRATION STIFFNESS MULTIPLIER = <real>
  USE ELASTIC UNLOADING = {NO|YES} (YES)
END [PARAMETERS FOR MODEL THOULESS_PARMIGIANI]