4.4.5. Directed Energy
Aria contains a number of directed energy (laser) source and flux models. The BEGIN DIRECTED ENERGY block in the Aria Region provides a unified way of specifying these sources and fluxes for a given configuration.
A directed energy model can be implemented as a surface flux, a source that penetrates into the surface, or a combination of the two. The typical inputs for a directed energy model are:
LASER POWER- The total power of the laser in Watts (for problems in SI MKS units). If there are multiple sources/fluxes specified the total power is divided among them based on their individual efficiency values (which must sum to 1).
PATH FUNCTION- A piecewise linear function for the time-varying position and orientation of the laser source.
ORIGIN AND NORMAL FUNCTION- A piecewise linear function for the time-varying position and orientation of the laser flux.
BEGIN X SOURCE- A sub-block defining a source model to use and its relevant parameters.
BEGIN X POWER WELD FLUX- A sub-block defining a flux model to use and its relevant parameters.
The complete set of commands for the directed energy model can be found in the directed energy command reference. An example input block is shown below for a case using both a source term and flux term in the same block.
BEGIN DIRECTED ENERGY MODEL bc2
laser_power = CONSTANT Value = 1500
add volume block_1 # for the source
path function = path1 # for the source
add surface surface_1 # for the flux
Origin and Normal function = path2 # for the flux
BEGIN Sharp Power Weld Flux
efficiency = 0.5
beam diameter = 0.20
END
BEGIN hemisphere source
efficiency = 0.5
beam diameter = 0.20
END
END
4.4.5.1. Laser Path
The movement of the laser source and flux are controlled by multicolumn user-defined functions, in the format shown below.
Begin Definition for Function my_path
Type is multicolumn piecewise linear
Column Titles Time X Y Z nx ny nz
Begin Values
0.0 2.2e-2 5e-3 1.5e-2 0 1 0
4.0 2.2e-2 1e-3 -1.5e-2 0 1 0
8.0 2.2e-2 1e-3 -1.5e-2 0 1 0
End
End
The laser sources/fluxes will follow the path defined by this function and the first and last rows of the table define the start and end times and positions. Outside those times, the laser is off and there is no source or flux.
Note
Both the PATH FUNCTION and ORIGIN AND NORMAL FUNCTION expect functions of this format. The PATH FUNCTION is used for sources while ORIGIN AND NORMAL FUNCTION is used for boundary fluxes.
Note
For laser fluxes the path normal vector should be the direction of the laser, and its orientation (towards or away from the surface) does not matter. The laser path origin should be the point where the laser originates from (so the laser vector is defined by the point and normal).
Note
For laser sources, the normal is optional and is used to define the source depth direction, and it should be pointed away from the surface (so the source depth is in the opposite direction as the normal). The laser path point is the center of the source (e.g. the center of the sphere for a spherical source).
4.4.5.2. Source Models
The various types of laser sources available are described in the following sections. For a complete list of the commands required for each model, refer to the directed energy command summary.
4.4.5.2.1. Hemispherical
The hemisphere model defines a hemispherical volume to heat the material block. If a Gaussian distribution is selected, the model is defined as:
where is the beam radius,
is the minimum distance from the evaluation point to the laser focal spot,
is the efficiency and
is the laser power. If the uniform distribution is selected, then the model is defined as:
The figure below shows a schematic of the hemispherical heating source.
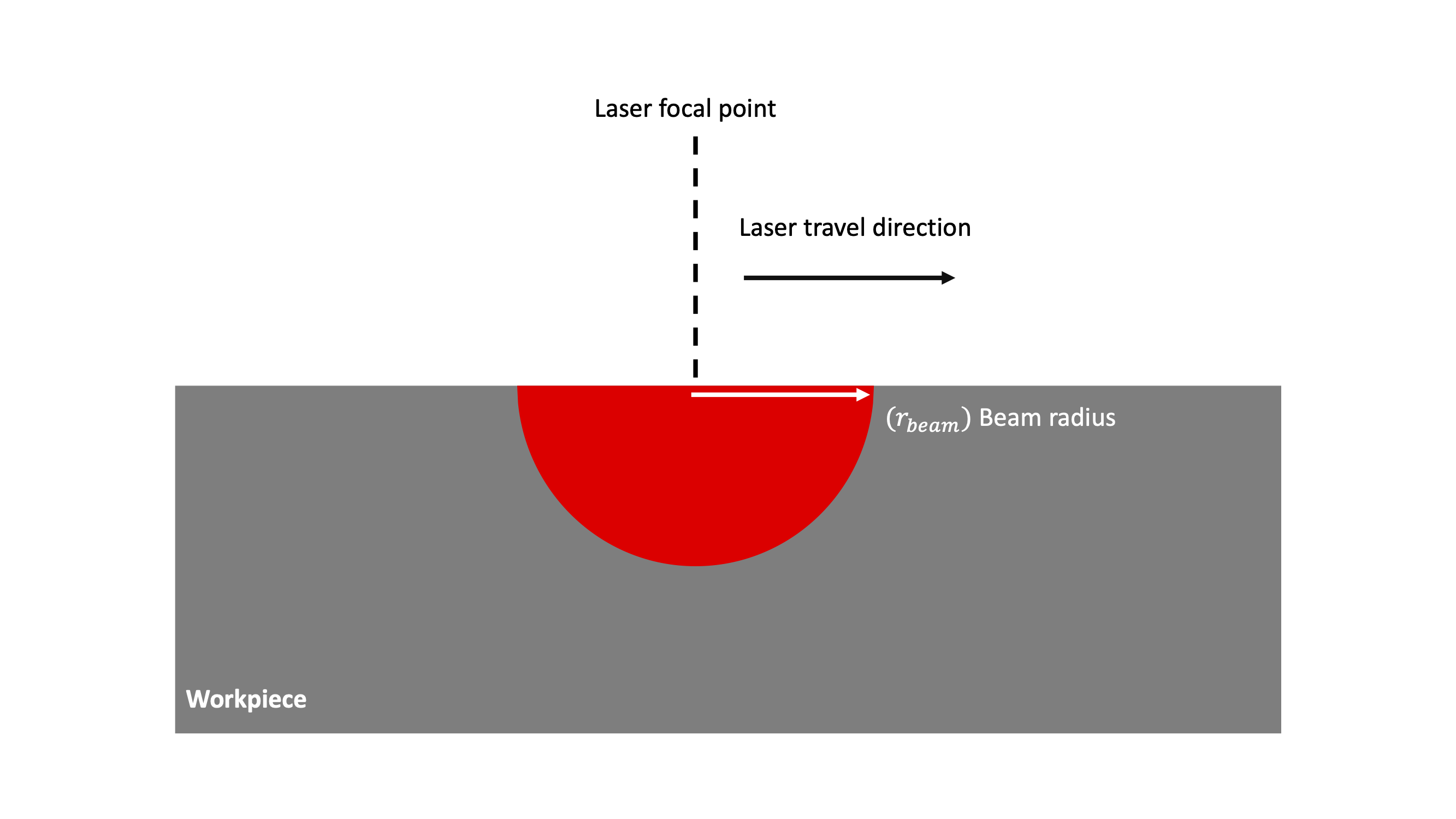
Fig. 4.19 Hemispherical source geometry.
4.4.5.2.2. Spherical
The sphere model defines a spherical volume to heat the material block. If a Gaussian distribution is selected, the model is defined as:
where is the beam radius,
is the minimum distance from the evaluation point to the laser focal spot,
is the efficiency and
is the laser power. If the uniform distribution is selected, then the model is defined as:
The figure below shows a schematic of the spherical heating source.
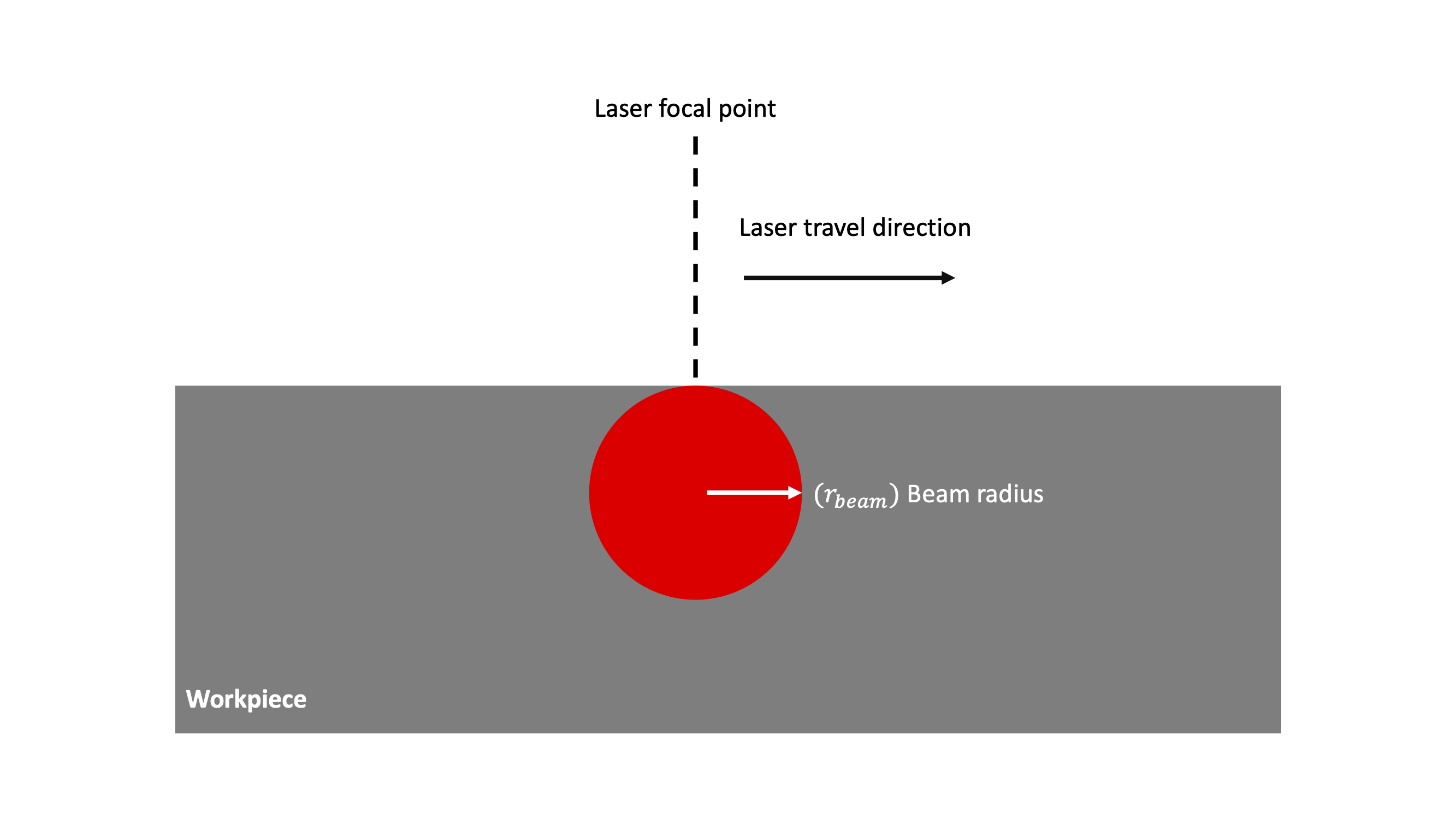
Fig. 4.20 Spherical source geometry.
4.4.5.2.3. Beer-Lambert
The Beer-Lambert model assumes an exponential decrease of the laser absorptivity with penetration depth. It is defined as:
where the effective beam radius,
is the beam radius
is the laser power,
is a spatial factor,
is the planar distance from the evaluation point to the laser focal point and
is an attenuation factor that varies exponentially with depth. The spatial factor
is an optional parameter defined by SPATIAL INFLUENCE FACTOR, and is given a default value of 1. The attenuation factor
is defined as:
where is an absorption coefficient (
) of range roughly 1 to 1e6 defined as a material property for the volume of interest. The value
is the
position of the laser focal point and
is the maximum penetration depth, which is currently defined as
. Surface absorption of energy can be accounted for by defining a modified attenuation factor
where
is the efficiency parameter.
4.4.5.2.4. Parallelpiped
The parallelpiped model is defined as:
where is the travel semi axis,
is the width semi axis,
is the penetration depth,
is the efficiency and
is the laser power. The parallelpiped assumes a uniform distribution. The figure below shows a schematic of the
parallelpiped heating source.
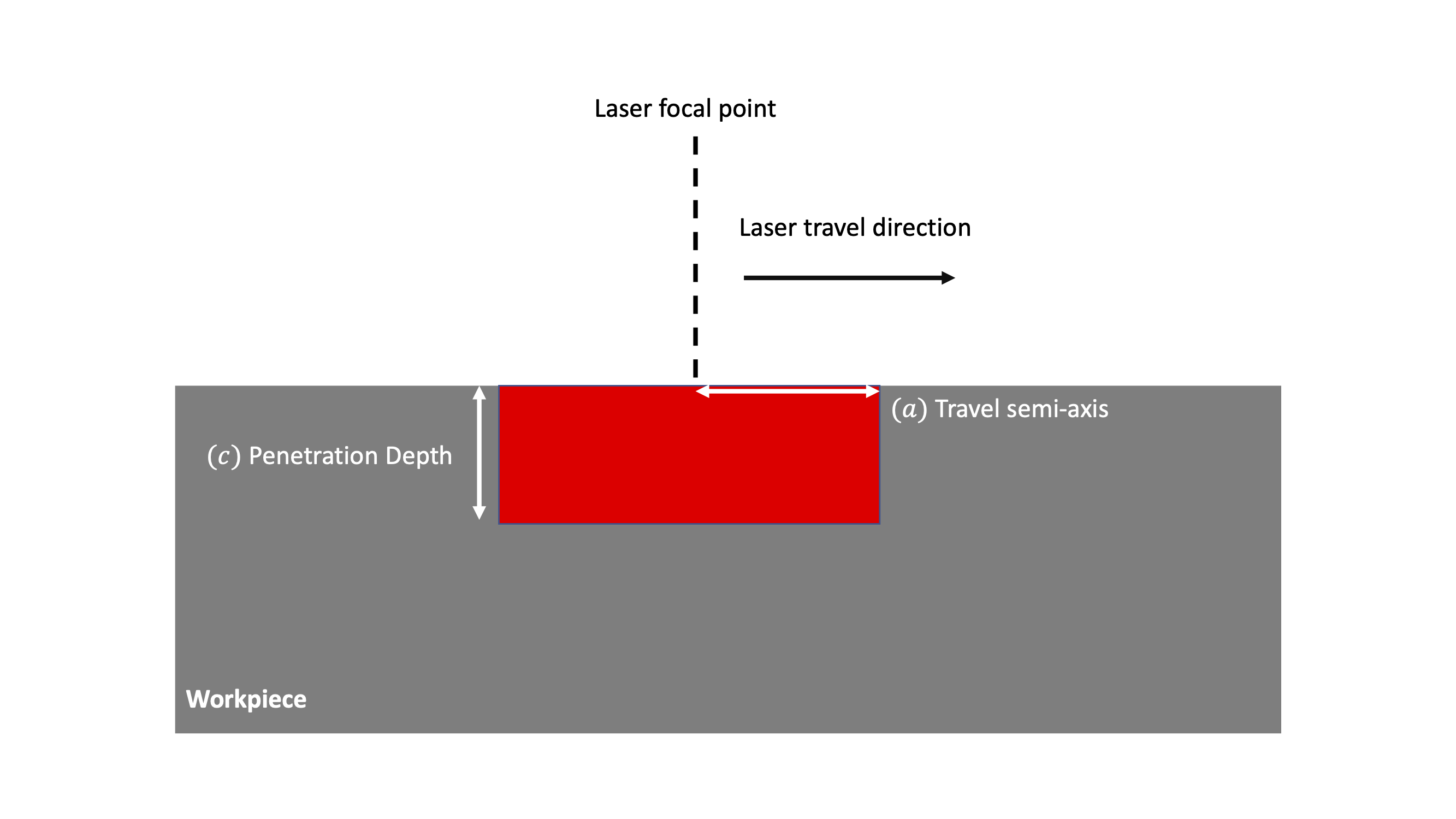
Fig. 4.21 Parallelpiped source geometry.
4.4.5.2.5. Ellipsoid
The ellipsoid model is defined as:
where is the travel semi-axis,
is the width semi-axis,
is the depth semi-axis,
is the efficiency,
is the laser power and
,
, and
are the
,
, and
coordinate of the laser focal point, respectively. The figure below shows a
schematic of the ellipsoid heating source, where the width semi-axis is pointing out of the page.
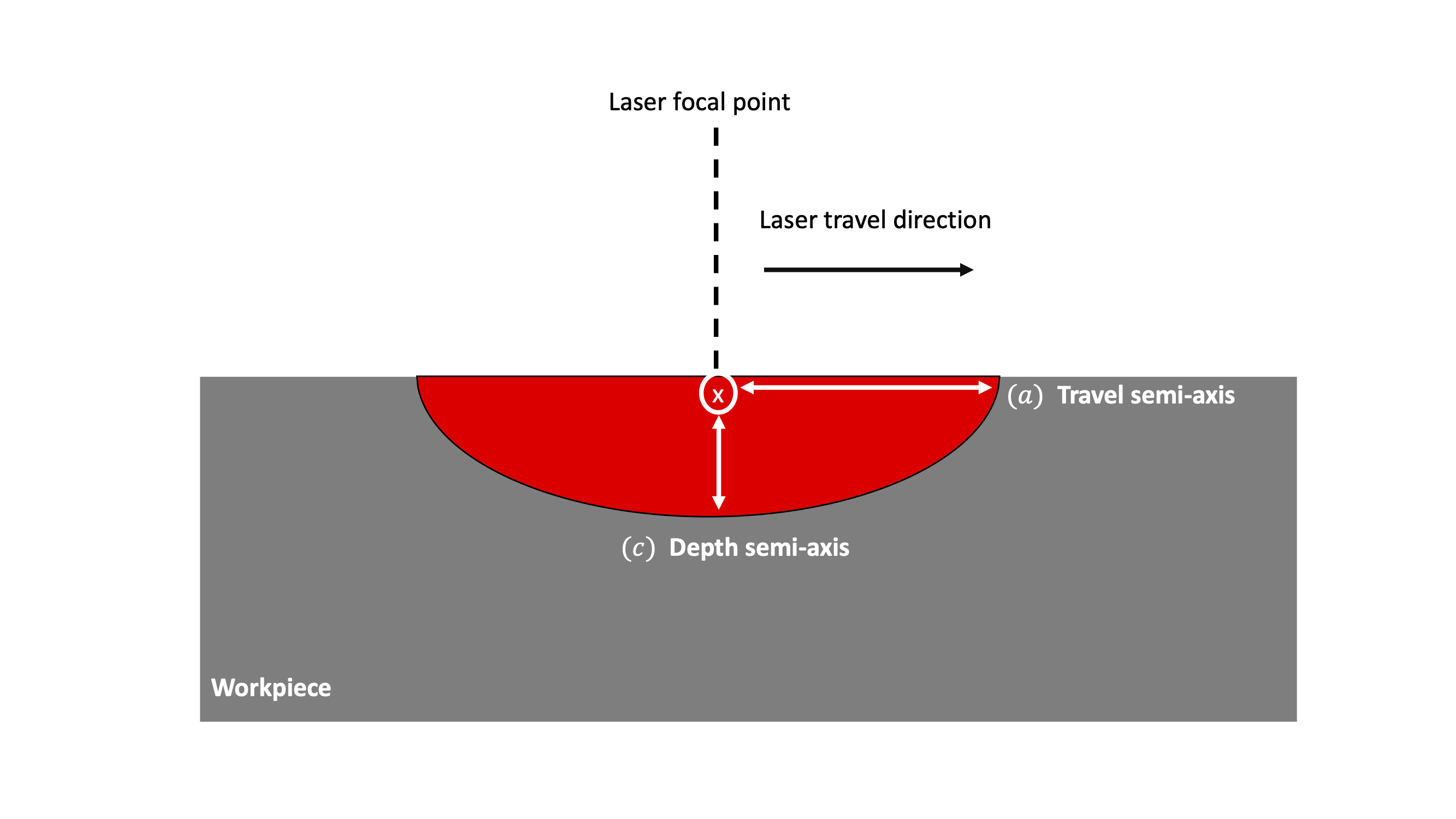
Fig. 4.22 Ellipsoid source geometry.
4.4.5.2.6. Double Ellipsoid
The double ellipsoid model defines two ellipsoid energy sources, and
combined at the laser focal point. The fore ellipsoidal energy source is defined as:
where is the fore travel semi-axis,
is the width semi-axis,
is the depth semi-axis,
is the fore power fraction,
is the efficiency
is the laser power, and
,
and
are the
,
and
coordinate of the laser focal point, respectively. The aft ellipsoidal energy source is defined as:
where is the fore travel semi-axis and
is the aft power fraction. The figure below shows a schematic of the double ellipsoid energy source model, where the width semi-axis is pointing out of the page.
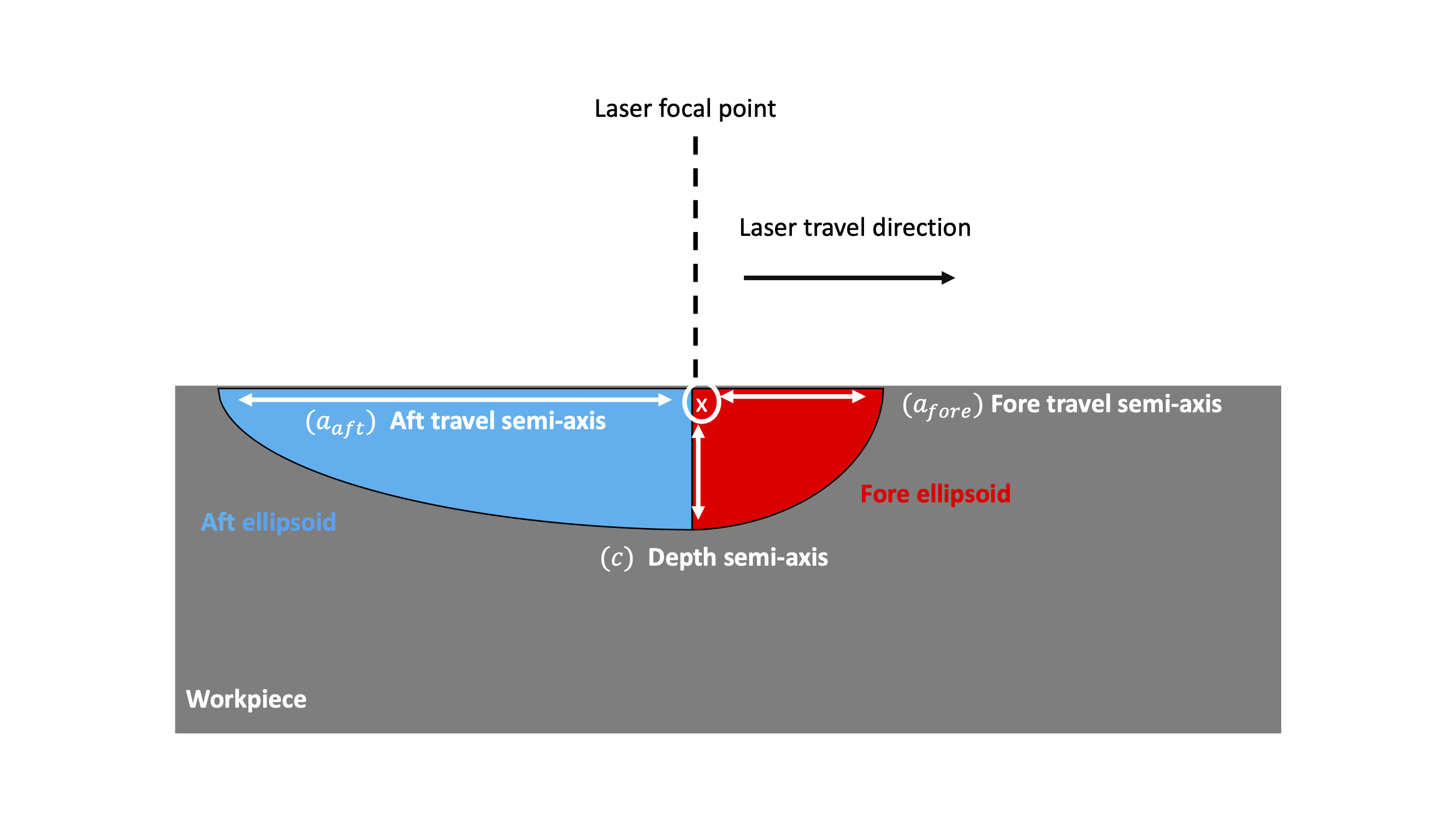
Fig. 4.23 Double ellipsoid source geometry.
4.4.5.2.7. Conical
The conical heat source model is defined as:
where is the efficiency,
is the penetration depth,
is the beam radius at the laser focal point,
is the beam radius at penetration depth
and
is the planar distance from the evaluation point to the laser focal point. The term
is the beam radius at a particular depth
, and is defined as:
where is the
position of the laser focal point. The figure below shows a schematic of the conical energy source model.
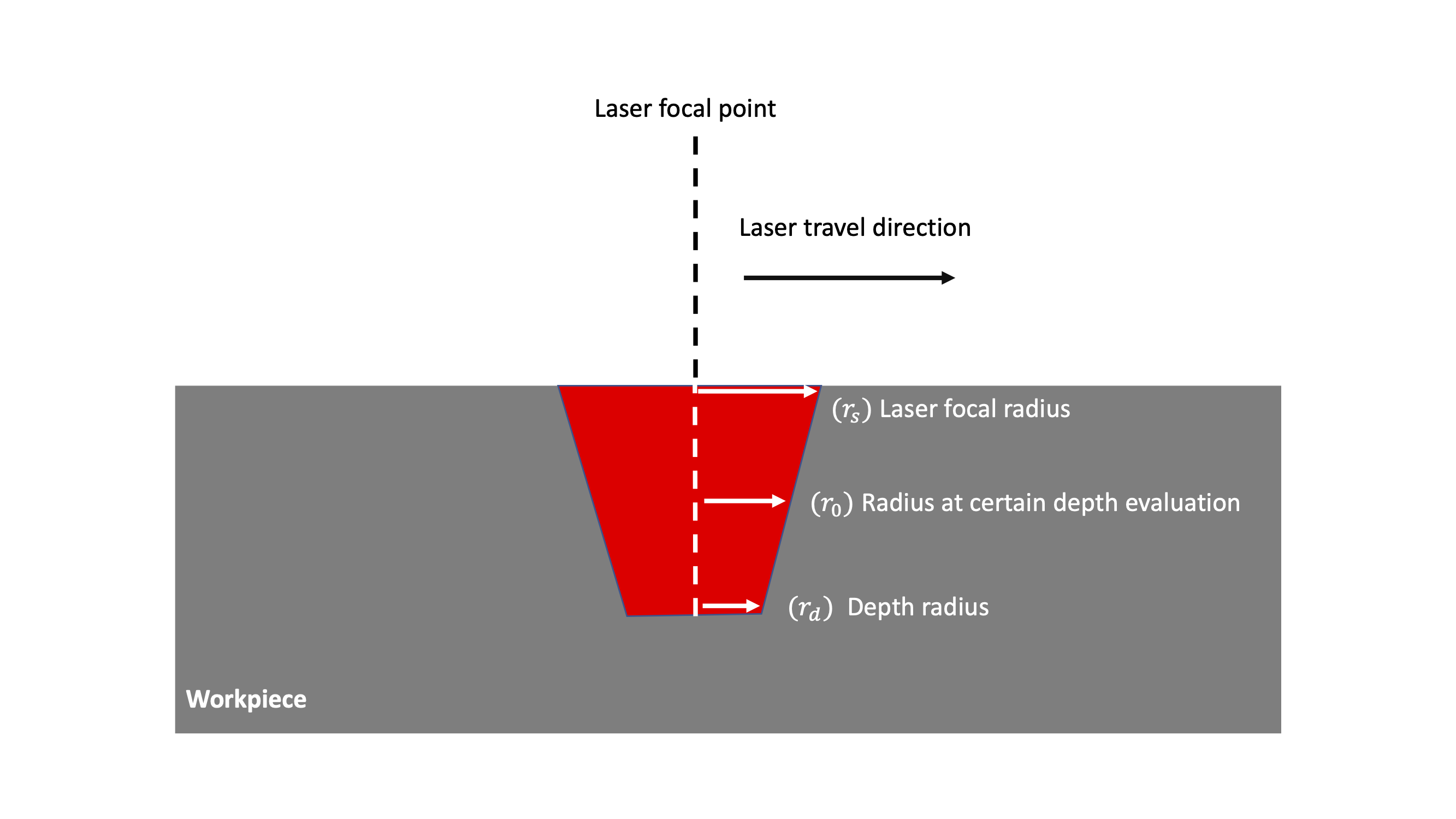
Fig. 4.24 Conical source geometry.
4.4.5.3. Flux Models
The various types of laser flux models available are described in the following sections. For a complete list of the commands required for each model, refer to the directed energy command summary.
4.4.5.3.2. Gaussian
The coordinates of the center of the beam are provided by the X, Y, and Z components of the provided origin_and_normal_function. The direction of the beam is provided by the NX, NY, and NZ components of the origin_and_normal_function. The applied flux is given by:
is the laser power defined for the material,
is the beam radius,
is the effective beam radius,
is the
laser absorptivity defined for the material,
is the
EFFICIENCY, and
is the shortest distance between a point on
the surface and the line defined by the beam origin and normal. The term
accounts for the fact that the surface may
not be orthogonal to the laser. Points with values of
>
CLIP_RADIUS will receive zero flux. If ACTIVATION is set to true, points
whose temperature exceed ACTIVATION_TEMPERATURE will be flagged as
activated for use with the ACTIVATION USER FUNCTION thermal conductivity
model. If INTEGRATED is true, this flux will be integrated between the
previous time step and the current one and the average flux applied.