6.6. Guidelines

The present section offers some useful guidelines for various user settings, which can be a useful starting point in setting up an analysis.

6.6.1. Initial Time Step Estimation for Thermal Problems

A method for estimating an appropriate initial time step is outlined below. This procedure is originally due to Levi ([51]) though it has been discussed by several other authors ([52, 53, 54]).

In the following development, it is assumed that a finite element mesh has been constructed that will adequately model the thermal phenomena of interest (e.g., thermal shock problems will require a fine mesh near a boundary while slower thermal transient will be less demanding on mesh refinement). For a given spatial discretization, a local characteristic length, $\Delta x$ , is chosen based on element size. Typically, this characteristic length is measured normal to a boundary on which a temperature or heat flux (source) disturbance occurs. Based on the characteristic length, the local heat transfer coefficient, $h$ , and the local thermal conductivity, $k$ , a local element Biot number ( $Bi = h \Delta x / k$ ) can be computed. Note that for a prescribed temperature, heat flux or heat source boundary condition, the heat transfer coefficient, $h$ , is assumed to be large leading to a large Biot number.

In order to bound the thermal gradient that will occur at the boundary in the first time step, the ratio of the temperature at a distance $\Delta x$ (characteristic length) from the boundary to the temperature on the boundary is selected. Let this ratio be defined by $\Theta = T (\Delta x)/T_{surface}$ . Typical values of $\Theta$ will range from 0.10 to 0.25. With the estimated values for local Biot number and temperature ratio $\Theta$ , a local Fourier number ( $Fo = \alpha \Delta t / \Delta x^2$ ) may be found from the charts in Fig. 6.1 and Fig. 6.1. These graphs are based on an analytic solution for one-dimensional conduction with a convective boundary condition ([55]). A value of the local Fourier number and values for the characteristic length and thermal diffusivity, $\alpha$ , then allow a time step to by computed.

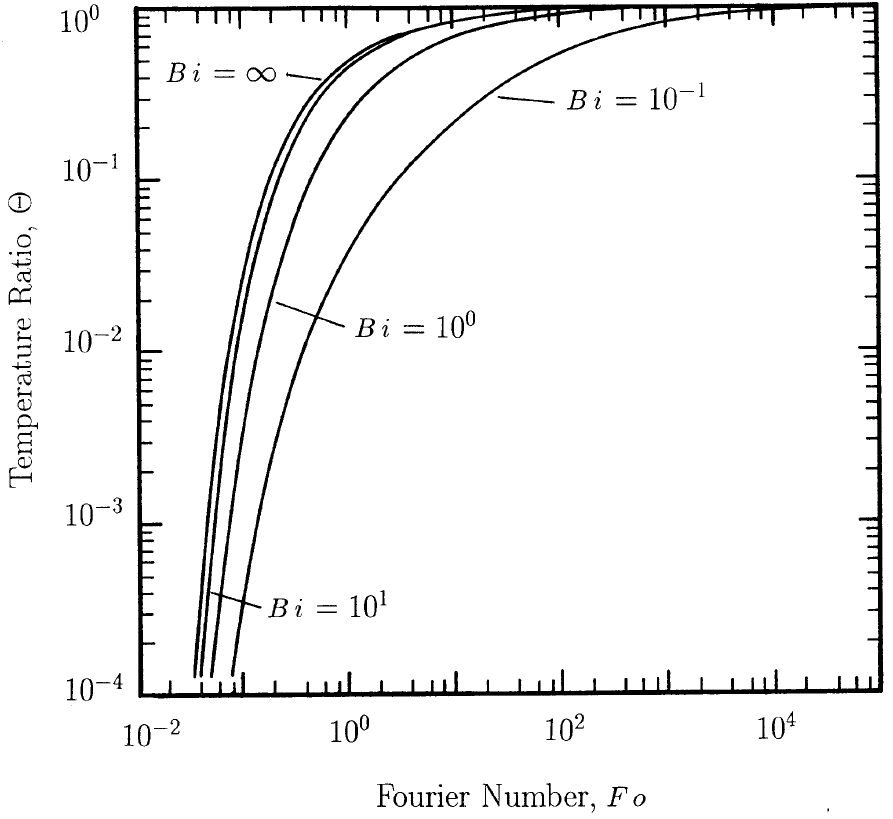
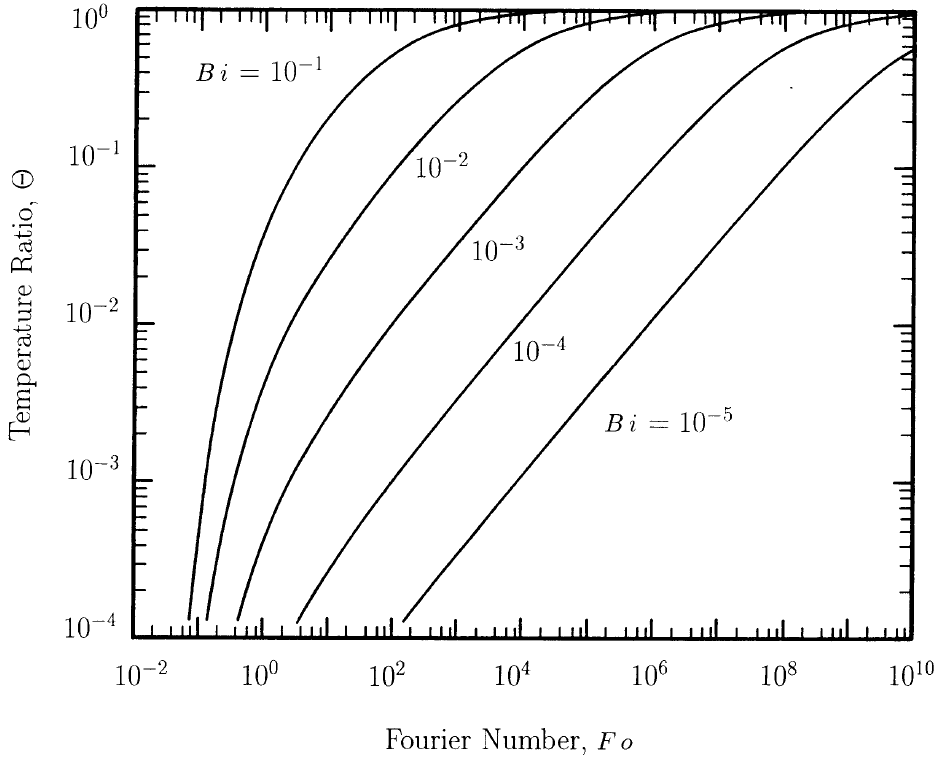
Fig. 6.1 Temperature ratio versus Fourier number for various Biot numbers

As an example of the procedure outlined above consider the transient problem described in the following example:

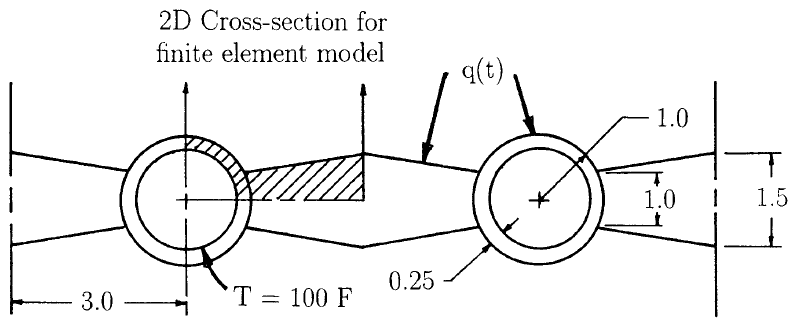
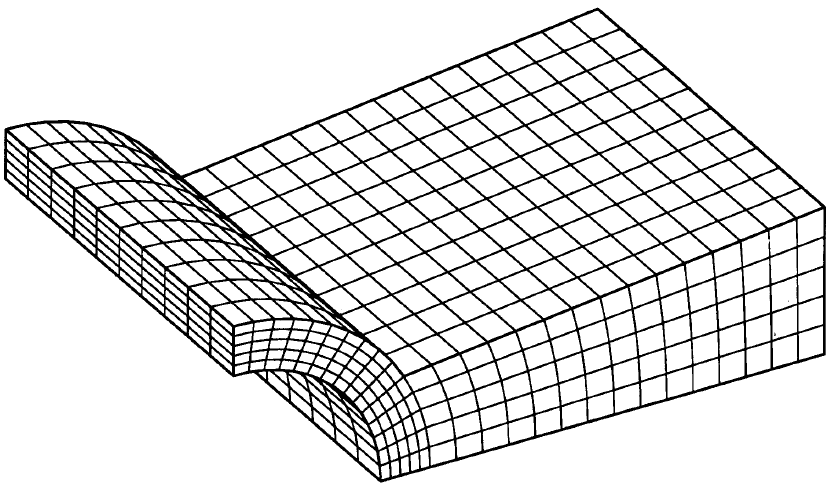
Geometry and mesh of finned radiator problem (Dimensions are in inches)

Consider the transient thermal response of a finned tube radiator, as shown in Finned Radiator. Thermal properties for the radiator are as follows:

$\rho = & 2.7071 \times 10^3 \text{kg/m}^3` \\ C = & 870.854 \text{J/kg} \cdot \text{K} \\ k = & 207.566 \text{W/m} \cdot \text{K} \\ \alpha = & 8.806 \times 10^{-5} \text{m}^2 \text{/s}$

The characteristic size is based in the average size of the elements along the radiator fin, as shown in Finned Radiator, and is equal to $\Delta x = 3.175 \times 10^{-3}$ m. The boundary condition is an applied heat flux, so the Biot number is assumed large (infinite). Using a temperature ratio of $\Theta = 0.10$ , then Fig. 6.1 yields a Fourier number of $Fo \approx 0.20$ . Thus,

$\Delta t = \frac{(Fo)(\Delta x^2)}{(\alpha)} = \frac{(0.20)(3.175 \times 10^{-3})^2}{(8.806 \times 10^{-5})} = 0.023 \text{ seconds.}$

The above procedure can also be used to estimate the overall response time for a region. In this case the length scale is a characteristic length for the entire region and the temperature ratio should be order unity. The Fourier number will then produce the approximate time interval required to reach equilibrium.