3.6. Radiation
3.6.1. Surface Radiation
A surface may exchange energy with its surroundings through thermal
radiation. Any incident surface radiation will be either transmitted,
reflected or absorbed. Letting ,
and
represent
the fractions of the incident flux in each category then
and for no transmission
Using the Kirchhoff identity
then the reflectance is
(3.100)
where is the emissivity.
In order to understand the radiative energy balance at a surface one considers the rate at which energy streams away from the surface, the radiosity, defined as
(3.101)
where is the blackbody emissive power and
is the irradiation.
Substituting for the reflectance (3.100) then
(3.102)
The surface flux is the difference between the energy that radiates away
and the incident energy
(3.103)
and substitution for the radiosity we find that
When is derived from an external temperature interaction
this boundary condition is often called far-field radiation, since it usually
models the radiative transfer of energy between a surface and the
external environment. However, the boundary condition is found
to have more general utility when one considers its role in
modeling radiative transfer between two surfaces,
&
,
as shown in Fig. 3.3, where
is
analogous to
.
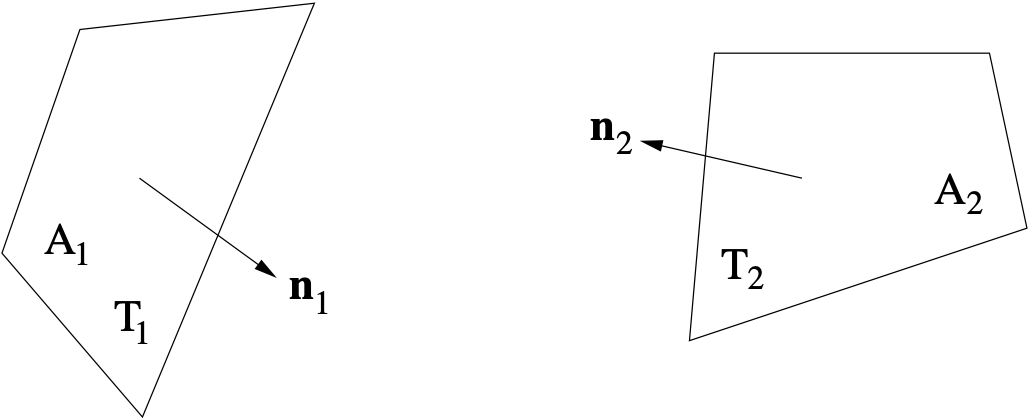
Fig. 3.3 Surface Radiative Exchange
For the case in which the temperature
is known and independent of temperature
then
using the emissive power
the normal flux per unit area across
may be written as
(3.104)
where denotes the Stefan-Boltzmann constant,
is the emissivity of the surface
and
is the form
factor. We remark that
(3.104) is a nonlinear boundary condition, since the
unknown temperature,
is raised to the fourth power and furthermore the
emissivity may be a function of temperature. It is important
to note that the form factor
may differ
from the more familiar view factor
encountered in
enclosure radiation problems. The question often asked is how does one
determine the appropriate value of form factor
.
The form factor can be best described using a
network analogy of radiative transfer between two surfaces as shown below.
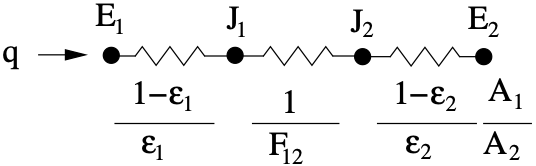
Fig. 3.4 Radiative Transfer Circuit Model
Using the emitted energy and radiosity
the network the heat flux can
be written in terms of a thermal resistance
as
(3.105)
and from the network model
For the third term of
can be neglected and
.
Comparing expressions (3.104) and (3.105) then
so estimation of is not required.
For (black receiving surface) but
and once again the third term of
can
be neglected so that
(3.106)
If both surfaces are black then
from the previous expression (3.106)
we find that
.
During a simulation the surface heat flux is integrated over the
spatial discretization of surface . Here we note that
defining the flux on a per unit area basis enables us to apply the
radiative flux (3.104) consistently with
evaluated
for the entire surface
even when the surface is discretized.
3.6.2. Enclosure Radiation
When energy radiates from one portion of a surface to another, and the intermediate medium is transparent (i.e., it does not absorb any energy), then enclosure radiation may be used to model the heat flux on the surface. Using the net radiation method [18], the normal flux at a particular location on the surface may be written as the difference between the emitted radiative heat flux leaving the surface, and the absorbed incident radiative flux due to the rest of the enclosure, namely
(3.107)
where denotes the absorptivity of the surface, and
represents the surface irradiation. Under the additional assumption
that the emissivity, absorptivity, and reflectivity are independent
of direction and wavelength, we may write
(3.108)
where is the reflectivity.
Without loss of generality, we can regard
the enclosure, , as a
union of
surfaces,
This situation is
illustrated in Fig. 3.6, where the radiosity for surface in the enclosure is defined to be
(3.109)
where is the area averaged constant temperature on facet
computed via
(3.110)
The surface irradiation for surface is determined by the radiosity
of all the other surfaces in the enclosure through the relation
(3.111)
where denotes the geometric viewfactor of surface
with respect to
surface
. The viewfactor may be considered as the fraction of energy that
leaves surface
and arrives at surface
. For a given pair of surfaces shown in Fig. 3.5,
the viewfactor is defined as the following integral
(3.112)
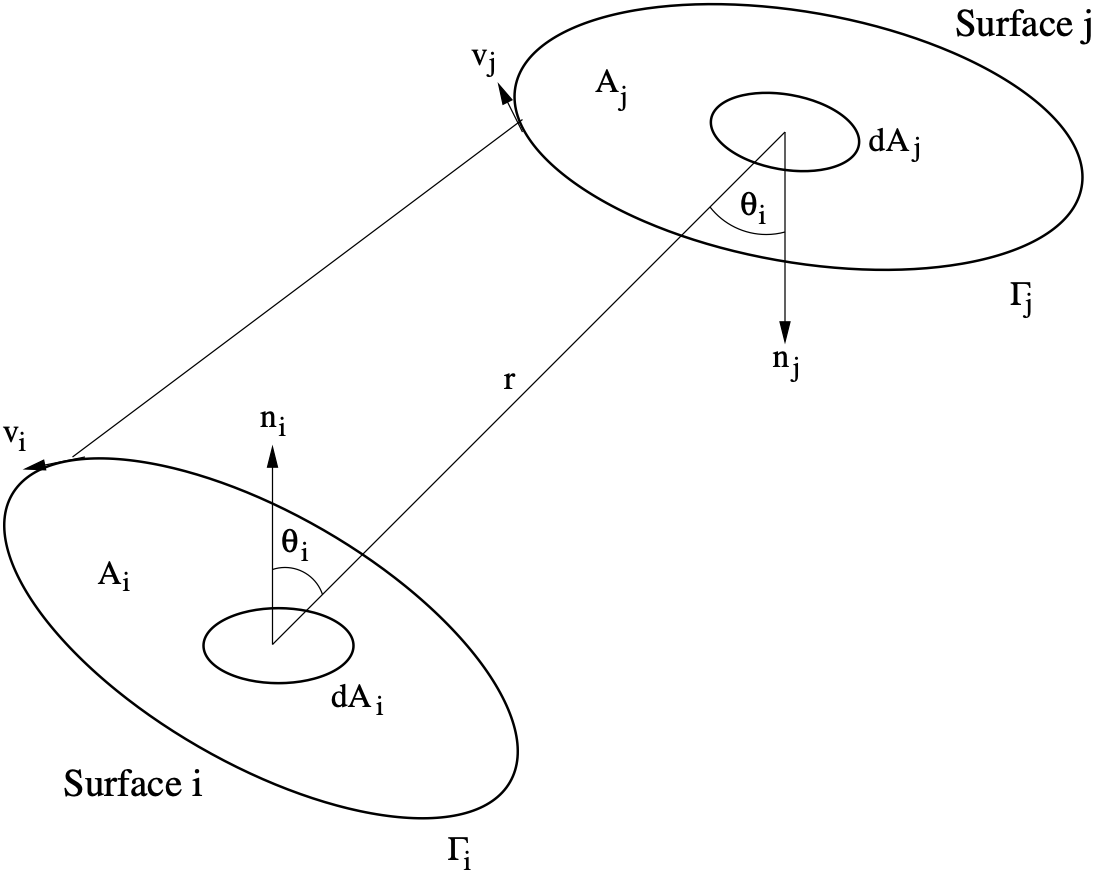
Fig. 3.5 Viewfactor Configuration.
Viewfactors are computed using the Chaparral library [19].
Determination of the viewfactors is a compute intensive endeavor. As such, extraneous calculations
are eliminated based upon the geometry. One example of this would be excluding this calculation for surfaces
which are not visible to each other. Moreover, from a geometric view of
enclosure surfaces, Fig. 3.5, one can conclude that
legitimate interactions between surfaces are those for which and
are opposed. Thus an important feature of the enclosure model is the notion of
inward facing normals. This convention effectively defines the interaction
between the enclosure subfacets.
Note
For closed surfaces (watertight enclosures), for each facet the
row-sum over all surface
facets should equal one, i.e.,
.
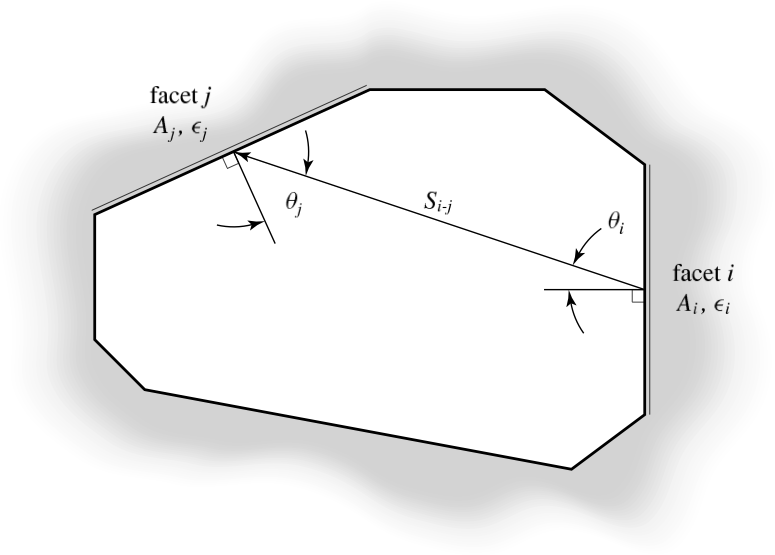
Fig. 3.6 Two arbitrary facets radiating energy to one another
in a radiation enclosure. The energy exchanged depends on:
the shape, orientation, distance, area ,
,
temperatures
,
, and radiative properties of the
facets
,
.
Upon substitution of equations (3.111) and (3.108) into (3.109), the radiosity may be written as
(3.113)
Finally, the first term in (3.113) may be moved inside the summation
to yield
(3.114)
where
(3.114) is a system of equations that can be solved for the unknown radiosity at each face.
Finally, we may rewrite (3.107) to express the radiative heat flux on
surface as
(3.115)
where is given by (3.111) and depends on the unknown radiosity.
This heat flux is applied as a boundary condition to the appropriate energy equations, thereby fully coupling
the enclosure radiation problem with the volume energy equations.
Instead of solving the monolithic equation system by forming the jacobian for the combined coupled system of equation systems, a segregated approach is used. At each nonlinear iteration, the radiosity equation is solved separately with the right hand side computed from the average facet temperature (3.110) using the current nonlinear temperature solution. Subsequently, the irradiation is computed from the radiosity in order to compute the heat flux contribution given by (3.115). A Newton step is then performed where the jacobian contribution of the radiative flux is computed as
(3.116)
where is the
nonlinear temperature residual,
the test function and where
(3.117)
Here, the facet temperature given by (3.110) has been relabeled to
to avoid confusion with the nodal finite element temperature solution. The sensitivity of the radiative
heat flux with respect to the facet temperature is approximated as
(3.118)
while the sensitivity of the facet temperature with respect to the nodal temperature dof is
(3.119)
where is the area of a facet. In terms of the element contribution, this can be compactly written
as
(3.120)
Note
The average facet temperature is . For computing the cube
, experience shows
projecting the raised power i.e.,
leads
to less spurious oscillations.
3.6.3. Banded Wavelength Enclosure Radiation
The enclosure radiation model previously presented considers a net response over all wavelengths assuming that all surfaces behave as grey bodies. Here the surface response with regard to different wavelengths is implicitly included in the model by using temperature dependent emissivities and allowing the surfaces to emit as grey bodies. In this case the surface flux previously mentioned (3.107) can be alternatively expressed as
(3.121)
In many applications engineering materials respond differently to different
portions of the thermal energy spectrum. Thus modeling the thermal radiation
response of these materials using the entire blackbody spectrum results in poor
characterization of the enclosure response. For this purpose more specialized
approaches for radiation modeling of wavelength dependent surfaces have been
developed using continuous representations of emissivity as a function of
wavelength and temperature while integrating over the wavelength spectrum. For
numerical modeling the simplest approach involves discretization of the
wavelength spectrum into a few representative bands and integrating over
each of the
bands. Using this approach the methods previously described
follow directly except that the emissivity and emissive power now have
independent representations in a wavelength band, each of which contributes some
surface flux
thus
(3.122)
Recalling that flux can also be expressed in terms of radiosity then similarly the radiosities are obtained by solving a system of equations
(3.123)
where is the incremental radiosity and
is the blackbody fraction for band
.
Finally we note that given a fixed facet temperature field this solution can be carried out
independently for each wavelength band and the radiosities
can
be accumulated to obtain the net facet radiosity
and net flux
.
Thus the banded wavelength model very much resembles the more simplified enclosure radiation model.
From a simulation point of view, the major difference being that the modeler must supply information describing
the band discretization in addition to emissivity models for each band.
Construction of the banded wavelength model begins by first prescribing the
emissivity variation for each surface of the enclosure as a function of
wavelength . The overall band discretization is then obtained by
collective consideration of the wavelengths at which the emissivity changes on
any of the given surfaces. Thus the number of bands for the enclosure will
likely be more than those for any single surface and is demonstrated in
Fig. 3.7 below.
Note
Each modeled band must have an emissivity model supplied for each surface, even when its emissivity is not changing.
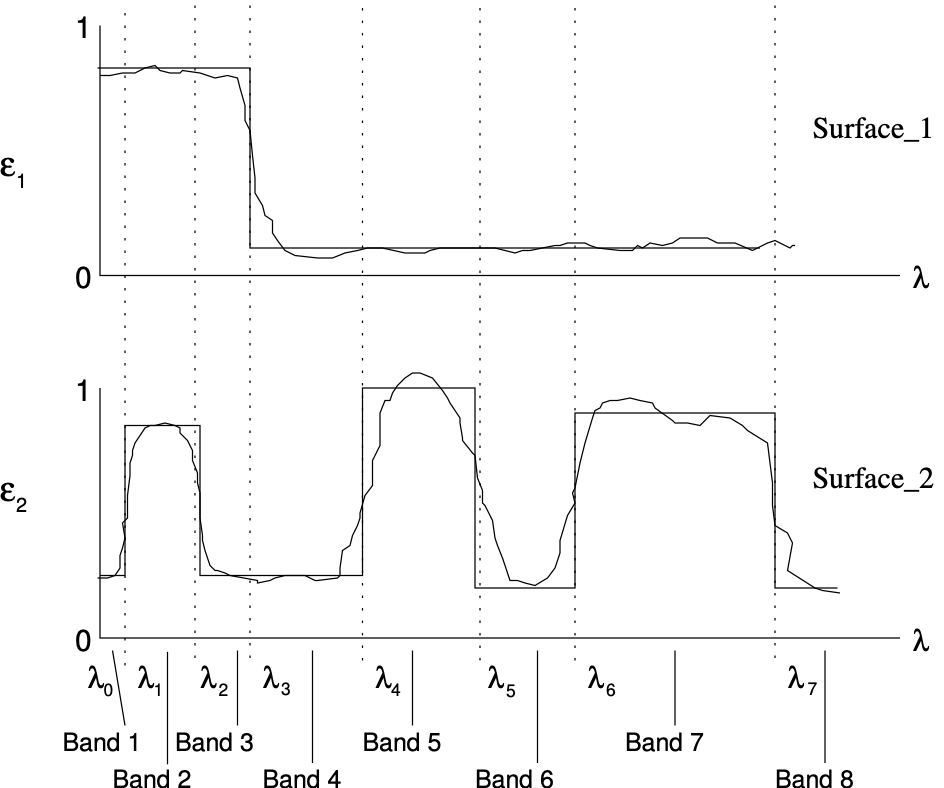
Fig. 3.7 Emissivity bands for two-surface problem.