Nonlocality, the incorporation of a length scale within the equations of mechanics, is increasingly recognized as an essential aspect of high-fidelity modeling of the fracture and failure of solids. The nonlocal peridynamic model, while providing the key advantage of unguided, autonomous crack growth, is computationally slower than the local finite element method, motivating the search for an accurate local-nonlocal coupling algorithm. Recently, under the LDRD project Strong Local-Nonlocal Coupling for Integrated Fracture Modeling, our team discovered a way to vary the length scale in different parts of a structure between zero (local) and positive (nonlocal) values seamlessly, minimizing artifacts and errors within the transition region.
Our approach is unique in that it is contained within the continuum, rather than discretized, mathematical system. As a continuum method, its advantages immediately carry over to any suitable discretization scheme or software that accurately solves the continuum equations. The method, which appears to be applicable to 3D and to nonlinear material response, promises to provide a mathematical tool for accurately and efficiently modeling the damage and fracture of complex solids and structures under dynamic loading.
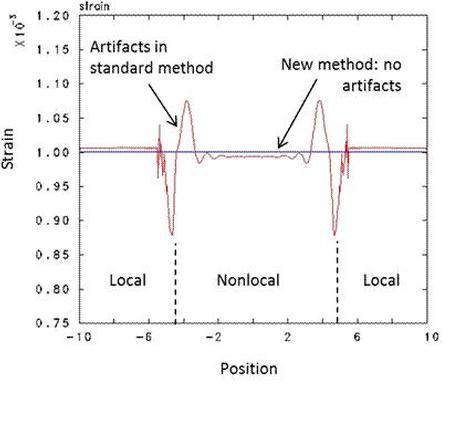
The figure below illustrates the absence of artifacts using the new method. The graph shows the predicted strain field in the stretching of a 1D elastic bar. The bar is partitioned into local and nonlocal subregions. With the new coupling method, there is zero error in the transition regions between local and nonlocal equations for this particular example problem.