Substantial and ongoing improvements to coupled models of the Earth system have steadily increased our ability to assess future global climate change. Providing quantified predictions of the impacts of global climate change on regional scales and human systems requires advanced global models that resolve multiple spatial scales, capture missing processes, and better quantify the uncertainties of model results. The U.S. Dept. of Energy has chartered the laboratories to develop an advanced Earth system modeling capability (ACME) to address these needs and has targeted DOE’s upcoming pre-exascale and future exascale computing systems.
Simulating the Earth system at the necessary spatial scales on these new architectures is driving much of the work in center 1400. The DOE LEAP project is focusing on the ACME model’s transport algorithms. Transport is a key subcomponent of the ACME atmosphere, ocean, and ice components, and represents the single most expensive computational kernel in the ACME system. The LEAP project is developing a new transport algorithm designed to run well on next generation architectures. The new algorithm combines a multi-moment approach to minimize interprocess communication with a characteristic trajectory algorithm to allow for significantly larger time-steps than with the current method. The implementation uses Kokkos to enable performance portability across traditional CPU systems and upcoming GPU and many-core systems.
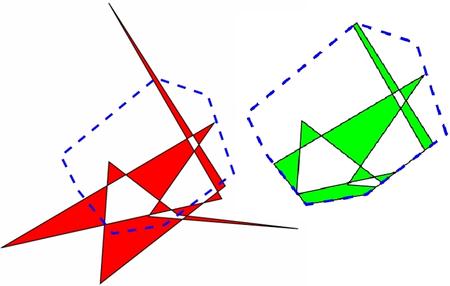
Important components of this transport algorithm are spherical polygon intersection and numerical quadrature over the resulting overlap polygons. A spherical polygon is a polygon projected onto a sphere such that the edges are great arcs. We have developed the library SIQK (Spherical Intersection and Quadrature with Kokkos) to provide these capabilities across architectures, including conventional CPU, Intel Xeon Phi, and Nvidia GPU. SIQK intersects an arbitrary (convex or nonconvex and possibly self-intersecting) spherical polygon against a convex polygon. This supports clipping an advected mesh cell against an Eulerian mesh cell. The resulting polygon can be partitioned into triangles, and then SIQK performs numerical quadrature over each triangle.