
The absorption, emission, and transport of radiative energy is an important effect in many kinds of simulations. Two cases of interest to Sandia are shown in these images -- simulating the effect of a fire on a waste or weapon container in an accident scenario, and simulating the implosion of a fuel pellet at the center of Sandia's Z-Pinch machine which is a prototype device for producing energy from nuclear fusion.


The radiation effects in these phenomena are described by the discrete ordinates form of the Boltzman equation. When discretized for a finite element grid, it describes the radiation flux of a particular energy as it passes through a grid cell with accompanying absorption, emission, and scattering. Including these effects is a large computational task because the radiative flux is a 3 dimensional quantity -- 2 angular directions and energy -- which must be solved for in each grid cell of the normal fluid or shock hydrodynamics model. This introduces as many as a few thousand extra unknowns per grid cell to solve for at each timestep.
On an unstructured grid, one way to solve the Boltzmann equation is to sweep the flux solution across the mesh in the direction of an individual discretized ordinate (angle). As shown in this figure, that gives rise to a directed graph where each vertex in the graph is a grid cell in the mesh, and edges point in the downwind direction between 2 adjacent grid cells.
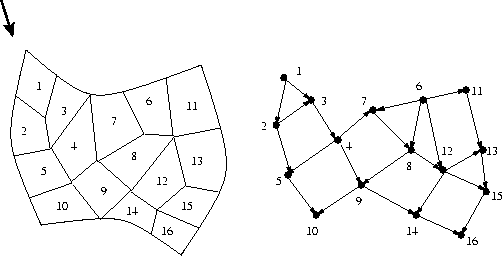
We've developed a parallel Boltzmann solver which allows multiple angles to be swept simultaneously on a grid/graph that is distributed across processors. This gives rise to an asynchronous parallel algorithm where small messages are passed from one processor to another as dependencies in the graphs are satisfied. The algorithm's scalability and load-balance is a function of how the grid is distributed across processors and the order in which work on each processor is scheduled. We are currently working to determine what options produce optimal parallel sweeping algorithms.
For deformed meshes such as those that occur in a Lagrangian hydrodynamics code (e.g. for the Z-Pinch simulations), these sweeping techinques also require that cycles in the directed graphs be detected and eliminated. Finding cycles in distributed directed graphs is an interesting algorithmic challenge that we have also been working on recently with collaborators at Texas A&M University. One of the papers below addresses this problem.
Collaborators on this project:
This paper overviews all of the parallel algorithms we developed, and highlights their performance on 2 large parallel machines:
Parallel Sn Sweeps on Unstructured Grids: Algorithms for Prioritization, Grid Partitioning, and Cycle-Detection, S. J. Plimpton, B. Hendrickson, S. Burns, W. Mclendon III, L. Rauchwerger, Nuclear Science and Engineering, 150, 267-283 (2005). (abstract)
This paper gives greater details about the parallel graph traversal algorithms:
Finding Strongly Connected Components in Distributed Graphs, W. McLendon, B. Hendrickson, S. J. Plimpton, L. Rauchwerger, J Parallel and Distributed Computing, 65, 901-910 (2005). (abstract)
This is a paper with details of our initial parallel sweeping algorithm for solving the Boltzmann equation and some performance results on the Intel Tflops machine:
Parallel Algorithms for Radiation Transport on Unstructured Grids, S. J. Plimpton, B. A. Hendrickson, S. P. Burns, W. McLendon III, Proc of SuperComputing 2000 (SC2000), Dallas, TX, November 2000. (abstract)
This paper discusses out initial parallel algorithm for cycle detection:
Identifying Strongly Connected Components in Parallel, W. McLendon III, B. Hendrickson, S. J. Plimpton, L. Rauchwerger, in Proc of SIAM Parallel Processing for Scientific Computing Conf, March 2001. (abstract)